A Walk Along the Dripline
For nuclear structure physicists, who examine why some atomic nuclei are shaped like footballs, pears, bananas, or just rigid spheres, the most revealing experiments are those that measure nuclei under extreme conditions. One such extreme is a nucleus that has so many neutrons relative to its number of protons that the outermost neutrons are just barely bound to the nuclear surface. On an isotope chart, the locus of isotopes to which no additional neutrons can be added is called the neutron dripline, and it is here that truly novel nuclear structure phenomena have been observed. Measuring these phenomena is one of the goals of the new Facility for Rare Isotope Beams (FRIB) presently being constructed at Michigan State University. In a paper [1] appearing in Physical Review Letters, Ryan Winkler and colleagues at the National Superconducting Cyclotron Laboratory, also housed at Michigan State, report work on radioactive, neutron-rich isotopes of argon that prepares the way for future measurements of dripline nuclei at FRIB and other planned radioactive beam facilities.
To see the variety of phenomena that occur at the neutron dripline, one can start at lithium and take a virtual walk along the most neutron rich isotopes of the light elements. Lithium- , which has four more neutrons than the heaviest stable lithium isotope and a half-life of only milliseconds, is a neutron dripline nucleus because it is the heaviest bound lithium isotope. The structure of this nucleus is an example of an exotic phenomenon called a two-neutron “halo,” in which the most weakly bound neutrons wander far (in a relative sense) from the “core” nucleus [2]. Carbon- , another neutron dripline nucleus, also has a two-neutron halo [3] (see 8 February 2010 Viewpoint).
Moving one proton up from carbon along the neutron dripline, nuclear behavior changes in a remarkable way. Nitrogen- and oxygen- , the dripline isotopes of those two elements, are considerably more tightly bound than carbon- , each having binding energies of a few mega-electron-volts. In fact, oxygen- seems to behave in many respects like a “doubly magic” nucleus, one with rigid closed shells of both protons and neutrons [4,5]. These three isotopes—carbon- , nitrogen- , and oxygen- —behave in very different ways, even though they all have an identical number ( ) of neutrons.
Moving again up one more proton from oxygen to the element fluorine, the dripline leaps out to neutron number (fluorine- ) [6]. Although fluorine- was first identified as a dripline nucleus in 1999, it wasn’t until 2010 that the anomalous dripline jump was explained by invoking three-nucleon forces [7], which had never been considered for any but the lightest nuclei. This theoretical breakthrough demonstrated how important it is for theory and experiment to advance in tandem in the study of nuclear structure.
Beyond fluorine, theoretical predictions of the dripline are available. According to calculations, the dripline nucleus for neon, the next element after fluorine, is the neon- nucleus, with neutrons. Calculations also predict that the dripline and near-dripline nuclei in elements heavier than neon exhibit a variety of interesting phenomena, such as “pygmy dipole resonances”, in which the proton and neutron fluids oscillate against each other (for example, see Ref. [8]); and neutron halo configurations, in which the shape of the halo is “decoupled” from the shape of the “core” nucleus [9]. But existing experimental facilities cannot produce these dripline and near-dripline isotopes—at least not in sufficient quantities to perform spectroscopic measurements.
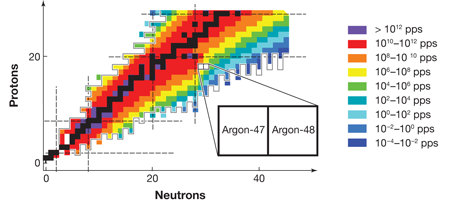
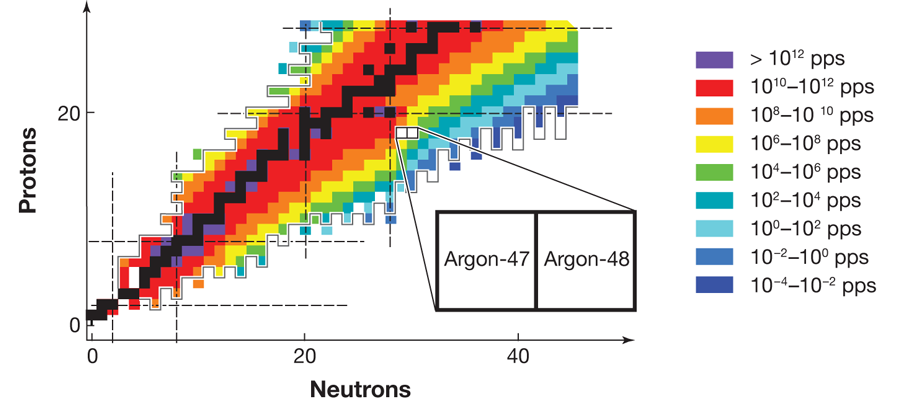
FRIB, which is expected to become operational before 2020, will be able to produce neutron dripline nuclei all the way up to argon ( protons). Figure 1 shows the estimated yield of radioactive isotopes at FRIB and the neutron dripline predicted by the KTUY mass formula [10], as well as the major shell closures for both protons and neutrons. The neutron dripline nuclei in elements near argon are particularly important because of the nature of nuclear shell closures. Nucleons (protons and neutrons) occupy orbits, just as electrons do in atoms. Orbits of similar energies form shells, once again just as they do for electrons in atoms. Shell closures, the “magic numbers” of protons and neutrons that give particular isotopes special stability, play a central role in our understanding of how nuclei behave. Moreover, the nature of shell closures changes in a particularly important way at neutron number . The magic numbers above , namely, , and , result from the nuclear “spin-orbit force,” which was identified more than sixty years ago and formed the basis of the Nobel-Prize-winning work on the nuclear shell model by Mayer and Jensen. To understand this force, it is critical to examine neutron dripline nuclei at neutron numbers of and higher, which exist only for elements heavier than fluorine, the limit for existing radioactive beam facilities. By providing access to dripline nuclei in elements up to argon, future radioactive beam facilities will throw the doors open to the examination of the forces that determine the behavior of all heavier nuclei.
However, simply producing neutron dripline isotopes up to argon will not be enough to ensure the success of future scientific programs with radioactive beams. It is critical to develop the experimental techniques to perform the spectroscopic measurements of these nuclei (even at FRIB, they will be produced in small quantities) and powerful theoretical tools with which to analyze the data.
It is in this context that the importance of the results of Winkler et al. on argon- and argon- can best be appreciated. To analyze the energy states of the argon nuclei, the team applied the experimental technique of intermediate energy Coulomb excitation, in which a nucleus inelastically scatters from another nucleus and the emitted gamma rays are analyzed to learn about the properties of the nucleus. This spectroscopic technique is, and will continue to be, a staple of nuclear structure studies at radioactive beam laboratories. Conventional experiments based on beams of stable isotopes generally deliver particles per second to a target. In comparison, the measurements reported by Winkler et al. on argon- , involve a beam rate that is million times smaller, with only particles per second. This and many other techniques in use at the National Superconducting Cyclotron Laboratory, which produce beams of exotic isotopes, detect gamma-ray photons, and identify beam particles, demonstrate tremendous progress toward the technologies that will be necessary for future dripline spectroscopy programs.
To analyze their data, Winkler et al. also confronted a daunting theoretical challenge that required them to take advantage of new shell-model tools. Traditionally, shell-model analyses have used calculations that involve only orbits within major shells, that is, between two magic numbers. For example, excellent work has been done during the last few decades on performing calculations in the shell between magic numbers and (the comes from the fact that the active orbits in between these two magic numbers are , , and —for example, see Ref. [11]). However, achieving an understanding of isotopes of silicon, sulfur, and argon close to the neutron dripline will require calculations that simultaneously treat the shell (between magic numbers and ) and the shell (between magic numbers and ). Winkler et al. compared two shell-model “interactions” that are competing to become the standard for calculations involving both of these shells, thereby establishing a framework to understand the observations made during future studies of dripline nuclei.
Altogether, the work on argon- and argon- pushes us a long way toward being prepared when FRIB and other radioactive beam facilities come online and the final spectroscopic assault on the neutron dripline for heavier elements begins.
References
- R. Winkler, A. Gade, T. Baugher, D. Bazin, B. A. Brown, T. Glasmacher, G. F. Grinyer, R. Meharchand, S. McDaniel, A. Ratkiewicz, and D. Weisshaar, Phys. Rev. Lett. 108, 182501 (2012)
- I. Tanihata, H. Hamagaki, O. Hashimoto, Y. Shida, N. Yoshikawa, K. Sugimoto, O. Yamakawa, T. Kobayashi, and N. Takahashi, Phys. Rev. Lett. 55, 2676 (1985)
- K. Tanaka et al., Phys. Rev. Lett. 104, 062701 (2010)
- C. R. Hoffman et al., Phys. Lett. B 672, 17 (2009)
- R. Kanungo et al., Phys. Rev. Lett. 102, 152501 (2009)
- H. Sakurai et al., Phys. Lett. B 448, 180 (1999)
- T. Otsuka, T. Suzuki, J. D. Holt, A. Schwenk, and Y. Akaishi, Phys. Rev. Lett. 105, 032501 (2010)
- T. Inakura, T. Nakatsukasa, and K. Yabana, Phys. Rev. C 84, 021302 (2011)
- S.-G. Zhou, J. Meng, P. Ring, and E.-G. Zhao, Phys. Rev. C 82, 011301 (2010)
- H. Koura, T. Tachibana, M. Uno, and M. Yamada, Prog. Theor. Phys. 113, 305 (2005)
- B. A. Brown and W. A. Richter, Phys. Rev. C 74, 034315 (2006)