Undoing a quantum measurement

Christoph Bruder; Daniel Loss

Viewpoint

Undoing a quantum measurement

Department of Physics, University of Basel, Klingelbergstrasse 82, CH-4056 Basel, Switzerland

November 10, 2008• Physics 1, 34

Quantum measurements are conventionally thought of as irretrievably “collapsing” a wave function to the observed state. However, experiments with superconducting qubits show that the partial collapse resulting from a weak continuous measurement can be restored.

Figure caption — **Figure 1:** (a) The projection of an object (i.e., its shadow) in general cannot be inverted to obtain the original object. (b) Simplified diagram of the phase qubit potential during the weak continuous measurement. State $| 1 〉$ tunnels out with probability $p$ , resulting in a detector click. A null measurement with no click will lead to a partial collapse of the initial state towards $| 0 〉$ . (c) After the first null measurement, a $π$ -pulse applied to the qubit flips the amplitudes of states $| 0 〉$ and $| 1 〉$ . The same measurement is now repeated. (d) If the result is also null, then a second $π$ -pulse will restore the qubit to its original state—the partial collapse of the wave function has been undone.

In quantum mechanics courses, students learn that the possible results of a quantum measurement of a physical quantity are the eigenvalues of the operator corresponding to the physical quantity. In other words, a measurement of the physical system “projects” it onto one of the eigenstates of this operator. In general, this only can happen in one direction: mathematically, the projection cannot be inverted, so it is an irreversible process. However, there are more gentle measurement schemes that only acquire partial information and so escape the constraint of traveling down this one-way street. A recent experiment on superconducting phase qubits performed by Nadav Katz and colleagues at University of California, Santa Barbara, and the University of California, Riverside [1], demonstrates that the effect of such a measurement can be “undone” and the initial state can be recovered.

Immediately after a measurement, the physical system will be in an eigenstate $| Ψ_{λ} 〉$ belonging to the eigenvalue $λ$ , which is the measured value of the observable property. Since the transition from the state before the measurement $| Ψ 〉$ to the state $| Ψ_{λ} 〉$ after the measurement is, mathematically speaking, a projection, there is in general no way of reconstructing $| Ψ 〉$ if you know $| Ψ_{λ} 〉$ (think of the shadow of a three-dimensional object on a screen, as in Fig. 1(a)—by just knowing a shadow, you cannot reconstruct the object). However, this type of measurement (a so-called strong or von Neumann measurement) is an idealized and extreme form of quantum measurement.

It has long been understood that not every quantum measurement can be described by von Neumann’s paradigm, which has come to be called the “collapse of the wave function” from $| Ψ 〉$ to $| Ψ_{λ} 〉$ . For instance, if you measure a current in a mesoscopic device, there is no single projection or collapse event, but many electrons passing a wire will successively build up the information that can be read out by an ammeter. Recently, however, there has been much interest in a different kind of quantum measurement called “weak” measurement. The idea of weak (continuous) measurements was developed in quantum optics [2]. Although these measurements yield only limited information about the system, they allow a continuous observation that will perturb the system only weakly. The transition from the initial state of the system to the final state after the measurement due to the acquisition of information during the measurement does not correspond to a projection. As a result, the measurement can be inverted, and the initial state of the system can be recovered.

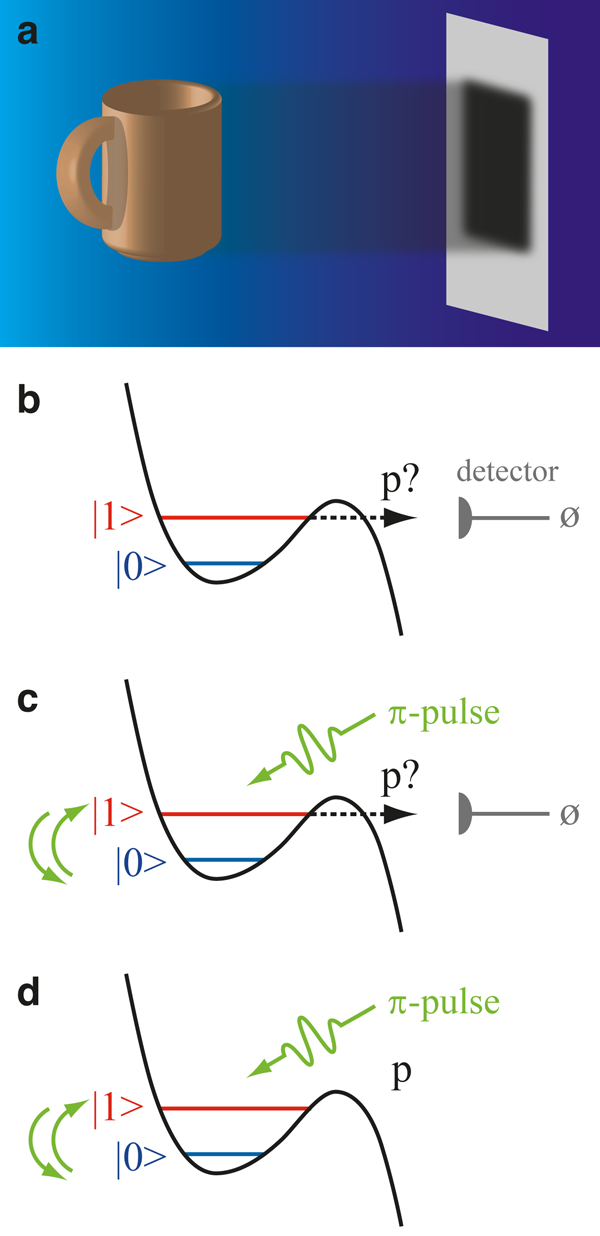
In the experiment carried out by Katz et al. [1], which is based on earlier theoretical work [3], this state recovery has been demonstrated for the first time. The system under consideration is a superconducting phase qubit—i.e., a superconducting loop containing a Josephson junction that can be considered as an effective two-level system [see Fig. 1(b)]. The qubit can be measured by a special type of detector that has the following properties: (i) if the qubit is in its upper (excited) state $| 1 〉$ , the detector will click with probability $p$ during the measurement interval, and (ii) it will never click if the qubit is in its lower (ground) state $| 0 〉$ .

If the detector does not click, we cannot be sure that the qubit is in its ground state. However, clearly we have acquired partial information (chances are higher than before the measurement that the qubit is in its ground state), and this information leads to a change of the state of the qubit compared to its initial state, namely a “partial collapse” towards $| 0 〉$ .

This partial collapse can now be undone in the following way [3]: After the first null-result measurement, swap the amplitudes of the states $| 0 〉$ and $| 1 〉$ by a special kind of stimulus called a $π$ -pulse [Fig. 1(c)]. (The $π$ -pulse or 180° pulse was originally devised to swap the high- and low-energy spin populations in NMR experiments.) Then apply a second measurement of the same type as the first one. If there is no detector click during the second measurement as well, i.e., if it happens to be again a null-result measurement, another $π$ -pulse will restore the qubit to the initial state it was in before both measurements [Fig. 1(d)]. Note the “if” in the last phrase: the procedure may not work—there may be a click during the second measurement. However, in the absence of a click during both measurements (which can be shown to happen with probability $1 - p$ ), we are guaranteed to get back the initial state.

One may wonder how all of this is compatible with the limiting case of a strong (von Neumann) measurement. A strong measurement corresponds to the limit $p \to 1$ : in this case, the probability of getting two consecutive null measurements (which is necessary for the reversal of the partial collapse) goes to zero. Hence the “uncollapsing” procedure will not be possible, which is consistent with the irreversibility of the strong measurement.

How did the authors implement the detector described above? The phase qubit can be thought of as a particle in the minimum of a cubic potential which has two (quasi-) bound states [see Fig. 1(b)]. The measurement corresponds to lowering the barrier height (by changing the Josephson junction bias current) for a well-defined time such that the particle will escape the well with probability $p$ if it is in the upper state. The escape probability for a particle in the lower state is negligibly small. The energy relaxation time and the dephasing time are significantly longer than the duration of the experiment, so relaxation and dephasing processes can be neglected.

To prove that this measurement scheme leads to a partial collapse of the initial state, Katz et al. used quantum tomography [4]. This is a procedure in which measurements are made on an ensemble of identical systems in order to collect a full picture of the state of the system, much like x-ray tomography where images from many angles are combined to create a 3D image. Similarly, at the end of the recovery procedure, quantum tomography was employed to check the fidelity of the whole process: the recovery procedure was repeated many times, and the $x$ , $y$ , and $z$ components of the “spin” of the qubit were measured to check whether the final state is equal or close to the initial state.

For probabilities $p \leq 0.6$ , the reversal fidelity, i.e., the overlap of the recovered state with the initial state, was found to be higher than 70%. The protocol begins to fail at larger $p$ , since energy relaxation processes to the ground state cannot be neglected any more. This surprising state recovery is (yet) another example that research on quantum computing and on experimental realizations of quantum bits leads to a better understanding of the foundations and the interpretation of quantum mechanics.

References

N. Katz, M. Neeley, M. Ansmann, R. C. Bialczak, M. Hofheinz, E. Lucero, A. O’Connell, H. Wang, A. N. Cleland, J. M. Martinis, and A. N. Korotkov, Phys. Rev. Lett. 101, 200401 (2008)
V.B. Braginsky and F.Y. Khalili, Quantum measurement [Amazon][WorldCat] (Cambridge University Press, Cambridge,1992)
A.N. Korotkov and A.N. Jordan, Phys. Rev. Lett. 97, 166805 (2006)
N. Katz et al., Science 312, 1498 (2006)

About the Authors

Christoph Bruder studied physics at Technische Universität München (Diploma 1985), the University of Sussex, and ETH Zürich (Ph.D. 1989). After postdoctoral fellowships at the University of Pennsylvania and the University of Karlsruhe, he was appointed Associate Professor of Physics (1998) and later Professor of Physics (2004) at the University of Basel. In 1997, he received the Klaus Tschira Award for Popular Science and in 2001, the Swiss-Korean Outstanding Research Efforts Award. From 2001 to 2007 he has served as a Divisional Editor of Physical Review Letters, and from 2004 to 2007 as a Co-Editor of Europhysics Letters. His main research interests include quantum coherence, quantum transport, ultracold atoms, and superconductivity.

Daniel Loss received his Diploma (1983) and Ph.D. (1985) in theoretical physics at the University of Zürich. From 1989 to 1991 he worked as a postdoc at the University of Illinois at Urbana-Champaign with A. J. Leggett, and from 1991 to 1993 at the IBM T.J. Watson Research Center, NY. In 1993 he joined the faculty of Simon Fraser University in Vancouver, and then returned to Switzerland in 1996 to become Professor of Physics at the University of Basel. His research interests include quantum coherence and spin physics in semiconducting and magnetic nanostructures, and quantum computing. In 2000 he became an APS Fellow and in 2005 he received the Humboldt Research Prize.

Reversal of the Weak Measurement of a Quantum State in a Superconducting Phase Qubit

Nadav Katz, Matthew Neeley, M. Ansmann, Radoslaw C. Bialczak, M. Hofheinz, Erik Lucero, A. O’Connell, H. Wang, A. N. Cleland, John M. Martinis, and Alexander N. Korotkov

Phys. Rev. Lett. 101, 200401 (2008)

Published November 10, 2008

Read PDF