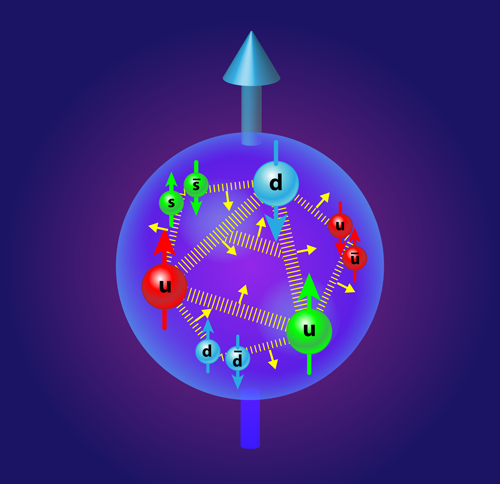
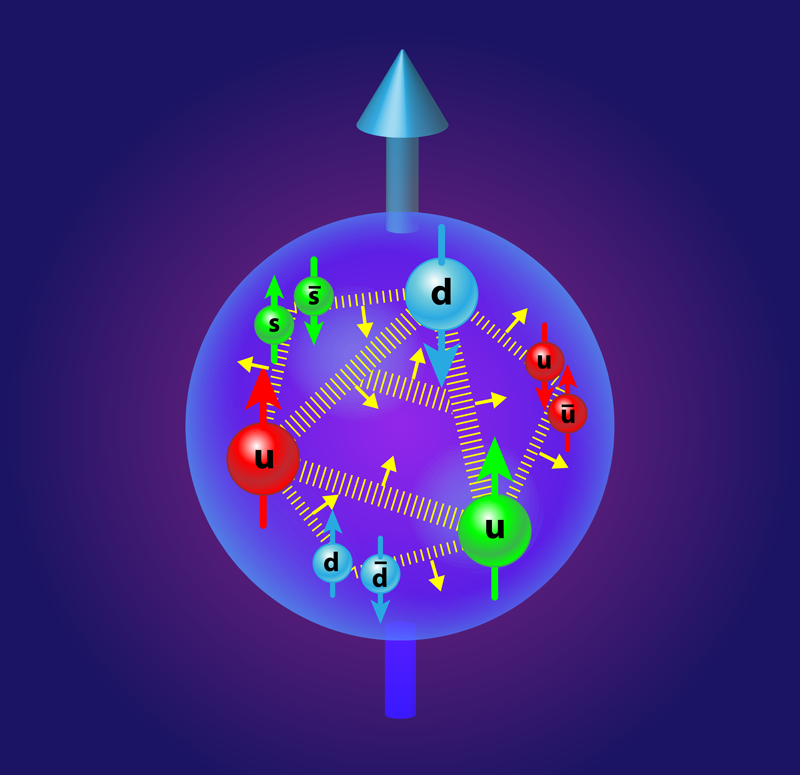
Spinning Gluons in the Proton

Steven D. Bass

Viewpoint

Spinning Gluons in the Proton

Marian Smoluchowski Institute of Physics, Jagiellonian University, 30-348 Krakow, Poland

March 6, 2017• Physics 10, 23

Computer simulations indicate that about 50% of the proton’s spin comes from the spin of the gluons that bind its quark constituents.

Figure caption — **Figure 1:** The spin of the proton is built up from the intrinsic spin and orbital angular momentum of its quark and gluon constituents.

Particle physics experiments conducted at the CERN, DESY, JLab, RHIC, and SLAC laboratories have revealed that only about 30% of the proton’s spin is carried by the spin of its quark constituents [1]. This discovery has inspired a 30-year global program of dedicated experiments and theoretical activity to understand the internal spin structure of the proton. But there are several questions. Why is the quark contribution to the proton’s spin so small? How much of the proton’s remaining “spin budget” is contributed by gluons, the particles that mediate the strong force between quarks (Fig. 1)? And how much is contributed by orbital angular momentum? Yi-Bo Yang from the University of Kentucky, Lexington, and colleagues now present the first theoretical calculation of the gluon contribution to the proton’s spin that uses state-of-the-art computer simulations of quark-gluon dynamics on a spacetime lattice [2]. Their new result suggests that gluon spin constitutes a substantial fraction of the proton’s spin.

Protons behave like spinning tops. But unlike the classical spin of a top, the spin of the proton and of other elementary particles is an intrinsic quantum phenomenon. This spin is responsible for many fundamental properties and phenomena, including the proton’s magnetic moment and the phases of low-temperature matter.

The proton is described in quantum chromodynamics (or QCD, the theory of quarks and gluons) by an inner core of three confined valence quarks and a sea of virtual quark-antiquark pairs and gluons, all surrounded by a diffuse cloud of virtual pions (light-mass bound states of a quark-antiquark pair). The relativistic motion of all of these particles means that they each carry orbital momentum. The spin of the proton is built up from the intrinsic spin of the valence and sea quarks (each 1/2) and the gluons (spin 1) and their orbital angular momentum, where spin is measured in units of Planck’s constant divided by $2 𝜋$ . The proton spin puzzle is the challenge to understand how these contributions combine to yield the total spin 1/2 of the proton.

High-energy particle-scattering experiments have found that the quark contribution to the proton (30%) comes entirely from the valence quarks; there’s just a very small contribution from the quark-antiquark sea [1]. The quark spin content deduced from these experiments could be so small for several reasons. First, the act of putting a relativistic particle, such as a quark, in a confining cavity, as is the case in the proton, generates some shift of total angular momentum from spin to orbital contributions. Second, gluon spin can screen the total quark spin contribution through a quantum effect called the axial anomaly [3]. Third, a topological effect can delocalize the quark spin inside the proton so that it is, in part, invisible to scattering on individual and localized quarks.

The study of the gluon spin, which is the focus of Yang and colleagues’ work, is useful in understanding both its share in the total spin budget and the size of the axial-anomaly effect. Experiments in the last decade at CERN and RHIC have provided valuable information on the proton’s gluon spin. The spin and orbital contributions to the proton’s spin depend on how deeply one probes inside the proton: what appears as a single valence quark at low resolution emerges at higher resolution as a valence quark surrounded by a sea of quark-antiquark pairs and gluons. These gluons will carry spin and orbital angular momentum. When one probes deeper inside the proton, and thus sees a greater number of gluons, the angular momentum summed over all of the proton’s constituent particles is always conserved. At the resolution scale of the experiments, one finds that gluons that carry more than 5% of the proton’s regular momentum contribute about $0.2 \pm 0.05$ units of spin to the spin-1/2 proton [4]. Early QCD-inspired models of the proton’s spin structure [5] and an early QCD spacetime lattice calculation [6] had suggested a gluon spin contribution of less than about 1 at the same scale, less accurate than present experiments.

In their study, Yang and co-workers have calculated the gluon spin contribution on a spacetime lattice using state-of-the-art computer simulations of QCD. The lattice calculations involve quarks with realistic small quark masses, close to their physical values, which is a major improvement on earlier work. They find a total gluon spin contribution of about $0.25 \pm 0.05$ at the same resolution scale as the experiments. Their number comes from gluons carrying the full range of regular momentum in the proton. Gluon spin at this resolution thus contributes about 50% of the proton’s spin—a substantial chunk of the total spin budget. This gluon spin contribution is, however, too small to play a major role in screening the size of the quark spin contribution through the axial-anomaly effect.

How does this result fit with our knowledge of the quark spin contribution? QCD-inspired models [7] and lattice calculations [8] of the quark spin contribution suggest a very small contribution from the sea quarks to the proton’s spin, in agreement with experiments. The small valence-quark spin contribution can be explained within the best present theoretical errors in terms of a shift of total angular momentum from the valence quarks into orbital angular momentum in the pion cloud. Taken together, the results on the quark and gluon contributions to the proton spin yield a self-consistent picture of the proton’s spin, based on the spin of the valence quarks, the gluon spin, orbital angular momentum (including that of the pion cloud), and perhaps an additional topological contribution. It is reassuring that QCD-inspired models, computational lattice calculations, and experimental data for both quarks and gluons give results in the same ballpark. With ever-improving computational power and techniques, one looks forward to having full calculations of the complete quark and gluon spin and orbital contributions to the proton’s spin from each theoretical group and lattice technique.

On the experimental side, more accurate information will hopefully follow from the electron-ion collider that is proposed for construction at either Brookhaven National Laboratory or at Jefferson Laboratory in the U.S. This project would allow one to measure the spin contribution from gluons carrying as little as 0.1% of the proton’s momentum (a 50-fold improvement over present experiments) with an error of about 0.05, as well as to make detailed studies of observables dependent on quark and gluon orbital angular momentum [9].

This research is published in Physical Review Letters.

References

C. A. Aidala, S. D. Bass, D. Hasch, and G. K. Mallot, “The Spin Structure of the Nucleon,” Rev. Mod. Phys. 85, 655 (2013).
Y-B. Yang, R. S. Sufian, A. Alexandru, T. Draper, M. J. Glatzmaier, K-F. Liu, and Y. Zhao, “Glue Spin and Helicity in the Proton From Lattice QCD,” Phys. Rev. Lett. 118, 102001 (2017).
G. Altarelli and G. G. Ross, “The Anomalous Gluon Contribution to Polarized Leptoproduction,” Phys. Lett. B 212, 391 (1988).
D. de Florian, R. Sassot, M. Stratmann, and W. Vogelsang, “Evidence for Polarization of Gluons in the Proton,” Phys. Rev. Lett. 113, 012001 (2014).
S. J. Brodsky, M. Burkardt, and I. Schmidt, “QCD Constraints on the Shape of Polarized Quark and Gluon Distributions,” Nucl. Phys. B 441, 197 (1995).
J. E. Mandula, “Lattice Simulation of the Anomalous Gluon Contribution to the Proton Spin,” Phys. Rev. Lett. 65, 1403 (1990).
S. D. Bass and A. W. Thomas, “The Nucleon’s Octet Axial-Charge $g_{A}^{(8)}$ with Chiral Corrections,” Phys. Lett. B 684, , 216 (2010).
G. S. Bali et al., “Strangeness Contribution to the Proton Spin from Lattice QCD,” Phys. Rev. Lett. 108, 222001 (2012).
A. Accardi et al., “Electron-Ion Collider: The Next QCD Frontier,” Eur. Phys. J. A 52, 268 (2016).

About the Author

Steven D. Bass is a Visiting Professor at the Jagiellonian University in Krakow, Poland. He is a theoretical particle physicist with interests spanning the QCD spin structure of the proton, eta-prime meson physics, and the cosmological-constant puzzle. Key research appointments have been as Research Fellow of Clare Hall, Cambridge, Alexander von Humboldt Foundation Fellow in Bonn, and Lise Meitner Fellow of the Austrian Science Fund in Innsbruck. He was awarded the Bragg Gold Medal of the Australian Institute of Physics for his Ph.D., which he completed at the University of Adelaide.