Measuring the Tidal Force on a Particle’s Matter Wave

Matt Jaffe; Holger Müller

Viewpoint

Measuring the Tidal Force on a Particle’s Matter Wave

Matt Jaffe

Department of Physics, University of California, Berkeley, CA 94720, USA

Holger Müller

Department of Physics, University of California, Berkeley, CA 94720, USA

May 1, 2017• Physics 10, 47

The effect of the tidal force, which is directly related to the curvature of spacetime, on an individual particle’s wave function has been measured with an atom interferometer.

Figure caption — **Figure 1:** Kasevich and colleagues [1] have measured the effect of the tidal force, and thus of spacetime curvature (illustrated in blue), on the wave function of individual particles using a “sensor” atom interferometer (green) and a “reference” atom interferometer (pink). Correlating the interference fringes of the two interferometers allowed cancelling the signal from Earth’s gravity and from vibrations of the setup. Varying the separation between the two arms of the sensor interferometer, while keeping the distance between the two interferometers constant, allowed demonstrating that the wave function of individual particles was influenced by the curvature of spacetime.

Atom interferometers have been used to make high-precision measurements in a diverse array of fields. Their more familiar optical counterparts, light interferometers, use matter elements such as mirrors and beam splitters to manipulate light waves. Atom interferometers invert these roles: laser pulses manipulate matter waves of atoms. These pulses split a matter wave into two, redirect the two resulting waves along different paths, and later recombine them to produce an interference pattern from which the measurements can be made. Now, Mark Kasevich from Stanford University, California, and colleagues [1] have used an atom interferometer to measure the effect of the tidal force—which is closely related to the curvature of spacetime and thereby to the fundamental description of gravity in general relativity—on an individual particle’s matter wave, or wave function.

The past two decades have seen stunning advances in the scope and utility of atom interferometers. These advances have been made through the development of ultracold atom sources that keep the atomic sample within the area illuminated by the laser pulses for longer periods of time, as well as development of powerful and versatile new lasers that can address multiple groups of atoms in rapid succession. With such atom sources and lasers, and an improved understanding of multiphoton light-atom interactions, it has become possible to use the momentum of tens and even hundreds of photons [2] to achieve meter-scale splittings [3] between the different paths taken by the matter waves. This has increased the sensitivity of atom interferometers by factors of hundreds or thousands, enabling numerous high-precision measurements. To name a few: measurements of gravitational acceleration [4, 5] with sensitivities of tens of $(nm ∕ s^{2}) ∕ {Hz}^{1 ∕ 2}$ ; measurements of fundamental constants, such as of Newton’s gravitational constant to an accuracy of 150 parts per million [6] and of the fine structure constant to about 0.7 parts per billion [7]; and stringent constraints on candidates for dark energy [8], which is thought to drive cosmic acceleration.

The tidal force of gravity, the focus of Kasevich and colleagues’ study, is the second spatial derivative of the gravitational potential. It is closely linked to the curvature of spacetime, the quantity that in general relativity describes the gravitational field. The gravitational potential itself is unmeasurable, while its first spatial derivative, the acceleration of free fall, is as much a function of the observer’s state of acceleration as it is a function of the gravitational field. For example, operating an atom interferometer in an accelerated frame of reference is the same as operating it in a gravitational field. The curvature, however, is a function only of the gravitational field and cannot be eliminated by going to a different frame of reference. Therefore, the curvature describes the gravitational field itself. Unlike phase shifts on a particle’s wave function arising from local acceleration, curvature-induced phase shifts may be described as an effect resulting purely from the influence of gravitation on a quantum system.

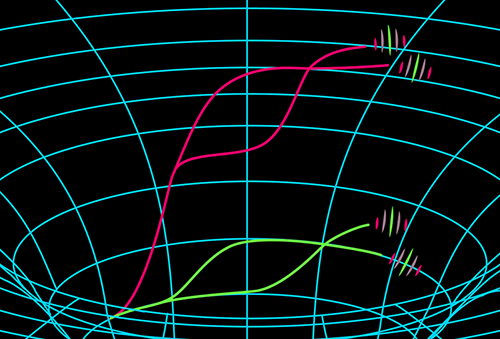
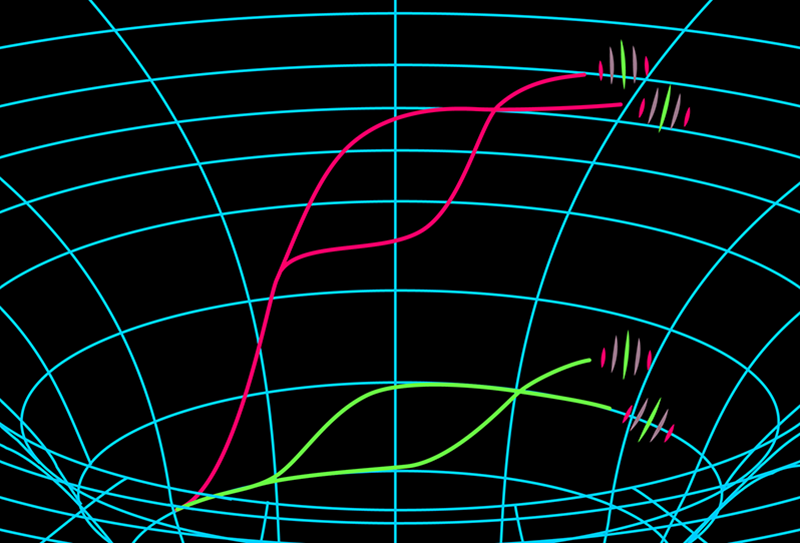
In their study, Kasevich and co-workers measured the effect of the tidal force, and thus of spacetime curvature, on the wave function of individual particles inside an atom interferometer. The measurement was possible thanks to a large separation between the interferometer’s arms (about 10 cm), which enhances the influence of curvature. A previous study has measured the differential effect of curvature on two separated atom interferometers [9]. Kasevich and colleagues generated the tidal force using moveable external source masses, which allowed them to discriminate against constant influences that could mimic the signal. Specifically, they cancelled the signal from Earth’s gravity and from vibrations of the setup by comparing the interference fringes of the interferometer with the ones of another interferometer that was located far enough away (about 30 cm) from the source masses to be largely insensitive to the curvature generated by them (Fig. 1). To show that they have indeed measured the effect of curvature on a single interferometer, the authors varied the separation between the interferometer’s arms, finding the characteristic quadratic dependence of the curvature signal on the separation.

The researchers used many of the above-mentioned advances in atom interferometry, many of which they have actually made themselves. They prepared a sample of about one million rubidium atoms at a temperature of 50 nK. They then launched the atoms upwards in a 10-m-high fountain configuration, which allowed a total free-fall time of up to 2.8 s, during which they could perform interferometry. Using the momentum of about 100 photons from dozens of laser pulses, they separated the spatial components of each individual atom’s wave function by about 30 cm. One of these two partial wave functions formed the “sensor” interferometer that measured the effect of curvature, while the other formed the “reference” interferometer that they used to cancel Earth’s gravity and the setup vibrations.

The apparatus allowed several feats to be achieved. First, the acceleration difference between the two interferometers was measured with an impressive precision of $0.6 nm ∕ s^{2}$ and a sensitivity of $5 \times 1 0^{- 9} m ∕ s^{2} ∕ {Hz}^{1 ∕ 2}$ . Second, the curvature generated by the artificial source masses (84 kg of lead bricks) caused as much as a 1-radian phase shift within the sensor interferometer, thanks to the wave-function separation in excess of 10 cm. Third, as noted, the experiment demonstrated the effect of curvature on the wave function of individual particles and showed that their wave function is coherent over the macroscopic scale of the sensor interferometer.

The results show how advances made over two decades have been synthesized into a high-sensitivity apparatus that can resolve miniscule changes in parameters such as accelerations. The next step in atom interferometry will be to test the equivalence principle and measure fundamental constants such as the fine-structure constant. But there’s more in store for atom interferometry, such as searches for ultralight dark matter candidates [10] and gravitational waves in the difficult-to-access 0.1–1 Hz band. Although these experiments will require even better capabilities (such as increased sensitivity and simultaneous use of different kinds of atoms), researchers are trying to achieve them with better modeling of systematic effects, construction of even more powerful lasers, and, especially for gravitational waves, even larger setups. We can expect further exciting news from atom interferometry for many years to come.

This research is published in Physical Review Letters.

References

P. Asenbaum, C. Overstreet, T. Kovachy, D. D. Brown, J. M. Hogan, and M. A. Kasevich, “Phase Shift in an Atom Interferometer Due to Spacetime Curvature Across Its Wave Function,” Phys. Rev. Lett. 118, 183602 (2017).
H. Müller, S.-w. Chiow, Q. Long, S. Herrmann, and S. Chu, “Atom Interferometry with up to 24-Photon-Momentum-Transfer Beam Splitters,” Phys. Rev. Lett. 100, 180405 (2008).
T. Kovachy, P. Asenbaum, C. Overstreet, C. A. Donnelly, S. M. Dickerson, A. Sugarbaker, J. M. Hogan, and M. A. Kasevich, “Quantum Superposition at the Half-Metre Scale,” Nature 528, 530 (2015).
A. Peters, K. Chung, and S. Chu, “Measurement of the Gravitational Acceleration by Dropping Atoms,” Nature 400, 849 (1999).
Z.-K. Hu, B.-L. Sun, X.-C. Duan, M.-K. Zhou, L.-L. Chen, S. Zhan, Q.-Z. Zhang, and J. Luo, “Demonstration of an Ultrahigh-Sensitivity Atom-Interferometry Absolute Gravimeter,” Phys. Rev. A 88, 43610 (2013).
G. Rosi, F. Sorrentino, L. Cacciapuoti, M. Prevedelli, and G. M. Tino, “Precision Measurement of the Newtonian Gravitational Constant Using Cold Atoms,” Nature 510, 518 (2014).
R. Bouchendira, P. Cladé, S. Guellati-Khélifa, F. Nez, and F. Biraben, “New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics,” Phys. Rev. Lett. 106, 080801 (2011).
P. Hamilton, M. Jaffe, P. Haslinger, Q. Simmons, H. Muller, and J. Khoury, “Atom-Interferometry Constraints on Dark Energy,” Science 349, 849 (2015).
G. Rosi, L. Cacciapuoti, F. Sorrentino, M. Menchetti, M. Prevedelli, and G. M. Tino, “Measurement of the Gravity-Field Curvature by Atom Interferometry,” Phys. Rev. Lett. 114, 013001 (2015).
P. W. Graham, D. E. Kaplan, J. Mardon, S. Rajendran, and W. A. Terrano, “Dark Matter Direct Detection with Accelerometers,” Phys. Rev. D 93, 075029 (2016).

About the Authors

Matt Jaffe is a Hellman Graduate Fellow in the Department of Physics at the University of California, Berkeley. He received B.S. degrees in Physics, Mathematics, and Engineering Science from Penn State University in 2012. For his Ph.D. research under Professor Holger Müller, he uses an atom interferometer in an optical cavity to search for dark energy candidates and to study interactions between atoms and a source mass. He plays professional ultimate frisbee with the San Jose Spiders of the AUDL.

Holger Müller is an Associate Professor of Physics at the University of California, Berkeley, and a Faculty Scientist in the Molecular Biophysics and Integrated Bioimaging Division of the Lawrence Berkeley National Laboratory. He did his undergraduate work at the University of Konstanz, Germany, and earned his Ph.D. from Humboldt University of Berlin, in 2004. As a postdoc, Müller was an Alexander von Humboldt fellow in the group of Steven Chu at Stanford, where he began studying atom interferometry. In 2009, he joined the physics faculty at UC Berkeley, where he leads a research group that uses matter-wave interferometry as both an applied technology and as a probe of fundamental physics.