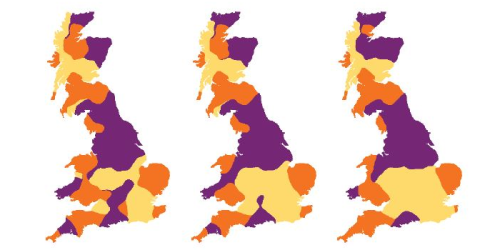
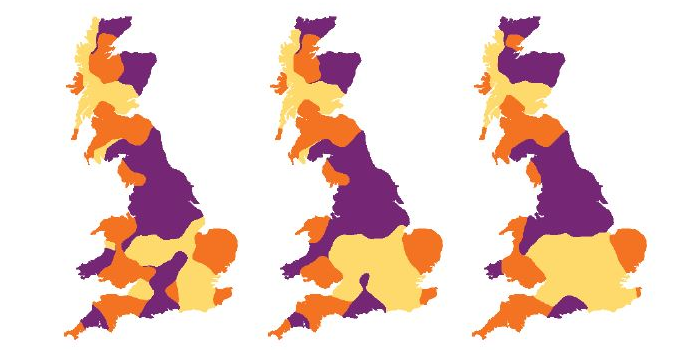
Language Boundaries Driven by Surface Tension
Human language is unique among communication systems in being a cultural system characterized by prodigious and pervasive variation and flux on many dimensions [1, 2]. Until the advent of global communication, linguistic varieties were predominantly localized to spatially bound areas, and much research in dialectology has been devoted to understanding the shape and distribution of these dialect regions and how linguistic change spreads through them. In a new paper [3], James Burridge from the University of Portsmouth, UK, presents an innovative statistical-mechanics model, in which the evolution of the boundaries between dialects is driven by a kind of “surface tension” that minimizes the boundary lengths. By accounting for the influence of external topographical features like the shape of coastlines and the positioning of cities, Burridge shows that his model reproduces established features in the distribution of dialects in Great Britain, Germany, and elsewhere.
The dynamics of linguistic variation and the mechanisms by which linguistic changes are propagated through communities have long been important issues for both historical linguists and sociolinguists wanting to explain the origin and evolution of languages. Traditional models of language dynamics used evolutionary trees to represent historical linguistic relationships, highlighting abrupt points of difference between languages but ignoring both the gradual nature of their divergence and any ongoing contact and mutual influence. An alternative “wave” model of linguistic diffusion [4] posited that linguistic innovations radiate from a central focus and vary in their adoption with distance from this source. Few examples of pure wave-like diffusion are found, however, and other researchers [5] instead proposed a hierarchical “gravity” model of diffusion to reflect the importance of population density in the spread of linguistic behavior. In this theory, innovations begin in heavily populated centers with greater interaction and cascade gradually through the system. Rather than a single wave, linguistic innovations jump between areas in order of population size, reaching sparsely populated areas later than densely populated ones, even when they are geographically closer to the original source. Later work [6], however, showed that diffusion patterns can vary dramatically for different linguistic features, depending on the social value attached to them. For example, adoption of a new word by a “popular” social group can sometimes help it spread more quickly [7, 8].
These models can be tested by looking for signatures in the spatial distribution of dialects. For example, the gravity model predicts that specific variants will be clumped around big cities. The spatial distribution of linguistic features was first noted by 19th-century dialectologists, who drew maps with boundary lines, or isoglosses, around the perimeter of areas using the same form for a linguistic item. Traditional dialect boundaries may therefore be seen on these maps where multiple isoglosses for different forms coincide. In practice, however, few dialect boundaries are precisely defined. Rather, they reflect transition zones of significant linguistic variability between distinct dialect regions [9]. A famous example is the so-called Rhenish fan in the dialect map of Germany. The main isogloss divides the country in half, with Low German in the north and High German in the south, but this boundary separates into at least eight different lines as it approaches the country’s western frontier—reflecting the significant linguistic variability among the large industrial centers situated along the river Rhine.
In his new study, Burridge presents a deliberately minimal model of language change, which focuses on explaining dialect distribution solely in terms of topographical features and speaker interaction. The model assumes the existence of multiple linguistic variants for multiple linguistic variables, which effectively define different dialects. In determining whether a given speaker adopts a specific variant, the model does not consider “social value” factors. Instead, it assumes that speakers interact predominantly with people living in their local environment (defined by some radius around their home), and that they will conform to the speech patterns of the majority of people in that geographic vicinity. Such local linguistic alignment favors the emergence of distinct dialect areas, with dialect boundaries tending to shorten in length in a way that mimics how surface tension minimizes the surface area of a water droplet (see Fig. 1). In a region with uniform population density, this language-based surface tension will cause the boundary between two dialects to form straight lines. Densely populated areas, however, interfere with boundary straightening by repelling boundaries and effectively creating new dialect areas around themselves. Furthermore, topography can have an imprint on dialect spatial distributions. In systems with irregular perimeters, Burridge shows that boundary lines tend to migrate to places where they emerge perpendicular from the edge of the system, such as indentations in coastlines.
The paper presents several artificial systems designed to reflect specific real-life topographies, with the results compared to known dialect-distribution effects. For example, the model shows how two large indentations on the English coast—a square-shaped bay called the Wash in the east and the Severn estuary in the southwest—can explain the major boundary between northern and southern English dialects. Over time, multiple isoglosses migrated to these indentations, thus reinforcing the differences between the two regions. The model is also able to simulate a Rhenish fan structure in an artificial system with a cluster of cities near the mouth of a river.
Burridge’s model successfully and feasibly reproduces several kinds of dialect distributions simply through local linguistic alignment in distinct topological circumstances. The author’s focus on a purely localized and geometric view of space between language users, however, can be seen both positively and negatively. On the plus side, it allows for a clear understanding of how minor changes in topology can yield very different dialect distributions in a qualitatively plausible way, and it opens the door for easy application of the model to other scenarios. But the model omits physical factors that contribute to a more nuanced view of the cultural “space” between groups of people in a community [9]. These include prestige factors, through which linguistic propagation is driven by the association of variants with different social groups [7, 8], and network factors that are known to profoundly affect the diffusion of change through different kinds of social networks [10].
This research is published in Physical Review X.
References
- N. Evans and S. C. Levinson, “The Myth of Language Universals: Language Diversity and its Importance for Cognitive Science,” Behav. Brain Sci. 32, 429 (2009).
- A. D. M. Smith, “Dynamic Models of Language Evolution: The Linguistic Perspective,” in The Palgrave Handbook of Economics and Language, edited by V. Ginsburgh and S. Weber (Palgrave MacMillan, New York, 2016), p. 61[Amazon][WorldCat].
- J. Burridge, “Spatial Evolution of Human Dialects,” Phys. Rev. X 7, 031008 (2017).
- L. Bloomfield, Language (Holt, Rinehart & Winston, New York, 1933).
- P. Trudgill, “Linguistic Change and Diffusion: Description and Explanation in Sociolinguistic Dialect Geography,” Lang. Soc. 3, 215 (1974).
- G. Bailey, T. Wikle, J. Tillery, and L. Sand, “Some Patterns Of Linguistic Diffusion,” Lang. Var. Change 5, 359 (1993).
- R. A. Blythe and W. Croft, “S-Curves and the Mechanisms of Propagation in Language Change,” Language 88, 269 (2012).
- T. Gong, L. Shuai, M. Tamariz, and G. Jäger, “Studying Language Change Using Price Equation and Pólya-urn Dynamics,” PLoS One 7, e33171 (2012).
- D. Britain, “Space and Spatial Diffusion,” in The Handbook of Language Variation and Change, edited by J. K. Chambers, P. Trudgill, and N. Schilling-Estes (Blackwell, Oxford, 2002), p. 603[Amazon][WorldCat].
- J. Milroy and L. Milroy, “Linguistic Change, Social Network and Speaker Innovation,” J. Linguist. 21, 339 (1985).