Solving Many-Body Problems with a Quantum Microscope
Elucidating the quantum behavior of large ensembles of interacting particles typically requires knowledge of the system’s many-body wave function. When the ensemble contains a few million atoms—typical for Bose-Einstein Condensates (BECs)—this is no mean feat. Sean Hodgman, from the Australian National University, and colleagues have now demonstrated a way to tackle this so-called quantum many-body problem that doesn’t require the wave function to be known. Their method instead determines all the parameters needed to characterize the system from measurements of the correlations between the momenta of individual atoms in the ensemble.
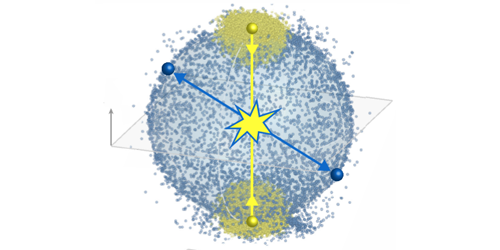
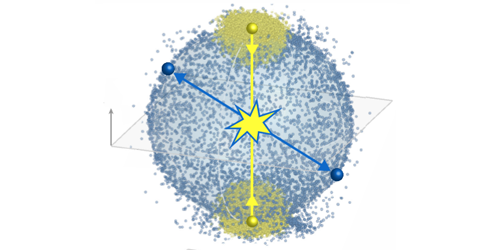
The researchers’ method involves recording the momenta of scattered atoms after two ensembles of BEC atoms are collided with one another. The atoms’ momenta obtained from such recordings are then used to calculate the correlations between all pairs and triplets of atoms in the scattered atom cloud. According to the group’s theoretical derivations and experimental measurements, these correlations are sufficient to solve the many-body problem for this system.
The team demonstrated their technique by smashing together two BECs, collectively containing one million helium atoms. Recording each atom’s position at various times after the collision, they reconstructed the atoms’ momenta and calculated the momentum correlation functions up to third order (three-atom correlations). Since the setup can map the atoms’ momenta in three dimensions, it can be regarded as a quantum many-body momentum microscope. Such a microscope could make it easier to study important many-body effects, including many-body localization phenomena and glassy behavior in highly disordered systems.
This research is published in Physical Review Letters.
–Katherine Wright
Katherine Wright is a Contributing Editor for Physics.