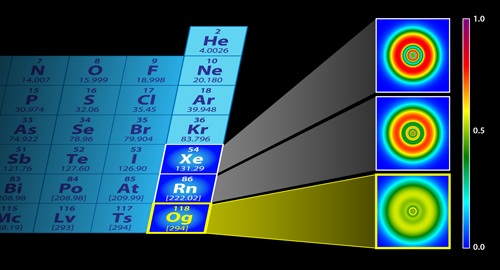
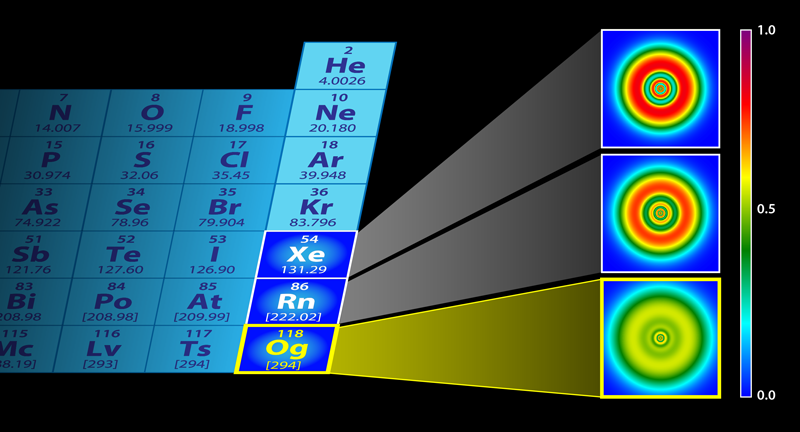
Heaviest Element Has Unusual Shell Structure
The periodic table continues to evolve, as it has since the publication of the first widely recognized periodic table by Dmitri Mendeleev in 1869. There have been over 700 versions of the table of elements to date [1], with elements regularly being added, filling empty blocks of the table. An example is the late 19th century addition of a new column (group) of elements, the noble gases, by William Ramsay, who received the 1904 Nobel Prize in Chemistry for his discovery [2]. The most recent entry to this column is oganesson (Og), which is the element with the highest known atomic number ( Z=118) [3]. This intriguing new element, which was first synthesized in 2002, completes the seventh row (7p block) of the periodic table and is the first superheavy ( Z>103) noble gas element.
A challenge in understanding oganesson and other superheavy elements is their short half-lives and low production rates. Oganesson has an estimated half-life of less than 1 ms, which is not enough time for most chemical observations. Instead, researchers must rely on atomic calculations to ascertain the fundamental properties of such a short-lived element. In a first for superheavy atoms, Paul Jerabek from Massey University Auckland, New Zealand, and colleagues have used fermion localization—a common method for visualizing electron or nucleon spatial distributions—to characterize the structure within oganesson [4]. They found that both the electrons and nucleons have a uniform distribution, which is in stark contrast to the nonuniform shell structure seen in lighter elements. This suggests that oganesson has chemical and physical properties that are very different from those of other noble gas elements.
It has long been known that the characteristics of the elements in the periodic table change significantly as the atomic number increases. For example, heavy elements experience lanthanide contraction, which is a shrinking of the atomic radius due to reduced shielding by inner-shell electrons of nuclear attractive forces on outer-shell electrons. As the atomic number increases, the impact of relativity also becomes more important, as inner-shell electrons move faster to avoid falling into the highly charged nucleus. This can have significant impact upon the manifestation of chemical and physical properties in elements from the lower half of the periodic table—the most common examples are gold, whose color arises because of relativistic effects [5], and mercury, whose very low melting point can be attributed to the impact of relativity [6].
There are other heavy-element behaviors that have been predicted but not yet observed. For example, it has been hypothesized that a transition will occur in the distribution (localization) of the electrons around the nucleus. For many elements, the electrons are located within specific shells that are separated by low-density bands. As the number of electrons increases, strong localization is expected to smooth out into a distribution resembling a Thomas-Fermi gas, which is a hypothetical, uniform-density gas based on a quantum-mechanical model of electron pairing. A similar transition—from a shell structure to a gas-like distribution—is expected to occur in the nuclei of heavy elements.
Jerabek et al. explored the electronic and nucleonic structure of oganesson, including the extent of localization. In order to investigate the electron density, for example, the team needed to consider electron-electron interactions, where the spin angular momentum and the orbital angular momentum for each electron interact and contribute to the total angular momentum for the atom. For elements with Z<30, this computation can be simplified by separately determining the overall orbital angular momentum ( L) and the overall spin angular momentum ( S) and then combining these terms into a single interaction (the LS, or Russell-Saunders, coupling).
For heavy elements, by contrast, the coupling of the spin angular momenta and orbital angular momenta for all electron becomes increasingly important. This leads to a complex electronic structure, as evidenced by the many transitions in the electronic spectra of heavy elements. To form the total angular momentum for the atom, the total angular momentum for each electron is considered first ( jj coupling). Jerabek et al. considered the impact of the transition from LS coupling to jj coupling in oganesson. For the electronic structure calculations, the authors utilized the Dirac equation of quantum mechanics rather than the nonrelativistic Schrödinger equation. The Dirac approach accounts for spin-orbit interactions ( jj coupling) and other relativistic effects.
To explore the shell structure, the team turned to fermion localization [7], which has proven to be a useful approach in understanding short-range behavior and shell separations. Fermion localization is based on the probability of finding two particles of the same type close to each other. Jerabek and colleagues generated two structure maps with fermion localization: one for electronic systems (called the electron localization function or ELF) and one for nuclear systems (called the nucleon localization function or NLF). This marks the very first application of fermion localization to a superheavy element.
From these calculations, the investigators noted an extraordinarily high value for spin-orbit coupling and demonstrated the very significant impact of relativistic effects upon the shell structure by comparing the ELF mapping for oganesson to that of lighter noble gases, xenon (Xe) and radon (Rn). The impact of relativistic effects on xenon and radon was limited, in contrast to oganesson, where the impact is extraordinarily significant (see Fig. 1). The atomic shell structure is barely discernible for oganesson, with the shells smeared out as in a homogeneous electron gas. As for the nuclear structure, the NLF calculated for the oganesson isotope ( 302Og) indicates reduced localization in comparison to NLF calculations for the lighter nucleus, 132Sn, considered in the study. This is consistent with previous findings [8] indicating changes in nucleonic shell structure of superheavy elements due to the large density and large electrostatic repulsion between protons. Clearly, the authors have demonstrated a transition to a Thomas-Fermi gas in both the electronic and nucleonic localization as atomic number increases.
Oganesson is a quite unusual noble gas element. In addition to its very large spin-orbit coupling and unique shell structure, the authors determined that oganesson has a rather large dipole polarizability and a positive electron affinity. From this, they inferred that oganesson should have increased van der Waals interactions in comparison to lighter noble gas elements. These important insights about the electronic and nucleonic shell structure of oganesson open the door to further theoretical investigation into its unusual properties. The remarkable results may also provide encouragement to experimentalists to develop instruments and experiments to enable further studies of the chemical and physical properties of superheavy elements.
This research is published in Physical Review Letters.
References
- E. R. Scerri, The Periodic Table: Its Story and Its Significance (Oxford University Press, New York, 2007)[Amazon][WorldCat].
- See, e.g., “The History of the Periodic Table,” Royal Society of Chemistry, http://www.rsc.org/education/teachers/resources/periodictable.
- Y. T. Oganessian et al., “Synthesis of the Isotopes of Elements 118 and 116 in the 249Cf and 245Cm + 48Ca Fusion Reactions,” Phys. Rev. C 74, 044602 (2006).
- P. Jerabek, B. Schuetrumpf, P. Schwerdtfeger, and W. Nazarewicz, “Electron and Nucleon Localization Functions of Oganesson: Approaching the Thomas-Fermi Limit,” Phys. Rev. Lett. 120, 053001 (2018).
- P. Pyykkö, “Theoretical Chemistry of Gold. III,” Chem. Soc. Rev. 37, 1967 (2008).
- F. Calvo, E Pahl, M. Wormit, and P. Schwerdtfeger, “Evidence for Low-Temperature Melting of Mercury Owing to Relativity,” Angew. Chem. 52, 7583 (2013).
- A. D. Becke and K. E. Edgecombe, “A Simple Measure of Electron Localization in Atomic and Molecular Systems,” J. Chem. Phys. 92, 5397 (1990).
- M. Bender, W. Nazarewicz, and P.-G. Reinhard, “Shell Stabilization of Super- and Hyperheavy Nuclei without Magic Gaps,” Phys. Lett. B 515, 42 (2001).