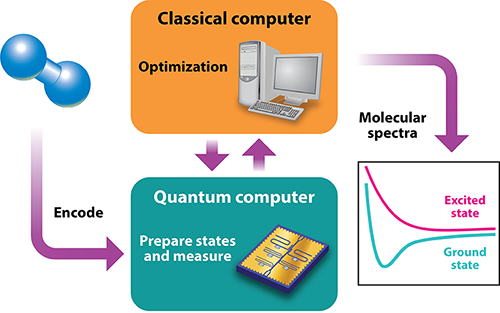
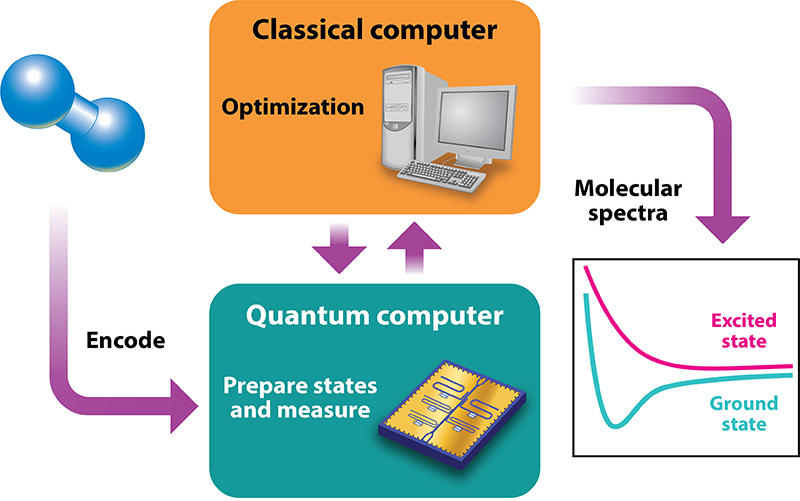
Quantum Computer Simulates Excited States of Molecule
One of the most promising and practical applications of quantum computing is quantum chemistry, in which the properties of molecules and materials are calculated from first principles. Compared with classical computers, quantum devices are expected to eventually perform quantum chemistry calculations more quickly and accurately, and they are also expected to handle much larger molecules. This quantum speedup could lead to the design and discovery of new pharmaceuticals, materials, and industrial catalysts. Fortunately, the pace of progress has exceeded expectations. In the last few years, researchers have used various quantum devices comprised of a few quantum bits (or “qubits”) to compute the ground-state energies of molecules, such as H2 and BeH2 [2–6]. Another important frontier is the simulation of excited states, which are fundamental to understanding a molecule’s absorption and emission of light as well as its chemical reactivity. James Colless of the University of California, Berkeley, and co-workers have advanced towards this goal by simulating the excited states of the hydrogen molecule ( H2) on a two-qubit processor (Fig. 1).
A key component of the work by Colless et al. is their use of an algorithm known as the variational quantum eigensolver (VQE). Like classical computer algorithms, a quantum algorithm provides a series of instructions for solving a computational problem, except that these instructions involve specialized manipulations for creating and altering quantum entanglement among qubits. Among existing quantum chemistry algorithms, VQE has attracted attention because it is expected to enable meaningful computations with relatively few qubits, using systems with modest coherence times. The algorithm is therefore well-suited for a number of existing and near-term quantum processors.
Notably, VQE is a hybrid quantum-classical algorithm, meaning it delegates tasks between quantum and classical devices. The quantum device “encodes” a trial molecular wave function into an assembly of qubits and estimates the wave function’s energy by performing measurements on the qubits. The classical processor then minimizes the estimated energy by adjusting the trial-wave-function parameters. The VQE algorithm is designed to be modular, such that the quantum and classical tasks can be modified or improved independently. Researchers (some of whom authored the new paper) recently took advantage of this versatility and formulated an augmented version of the VQE algorithm that can be used to approximate a molecule’s excited-state energies [7]. The work by Colless et al. marks the first demonstration of this new algorithm, known as quantum subspace expansion (QSE), on a quantum processor.
The QSE algorithm works as follows. It takes as its input the ground state |𝜓〉of a molecule, which is determined by a standard VQE procedure. The algorithm then approximates a “subspace” of low-energy excited states from linear combinations of states of the form Oi|𝜓〉, where the Oi are physically motivated quantum operators. Specifically, the chosen combination of operators should correspond to exciting an electron to a low-energy excited state of a molecule. Finding the linear combination for each excited state requires filling in the matrix of energy expectation values, 〈𝜓|OiHOj|𝜓〉, where H is the Hamiltonian operator. This task is accomplished by the quantum part of the computation. The classical counterpart then diagonalizes the matrix to find the energies of the excited states. Although other quantum computational methods exist for simulating excited states, QSE is one of the least expensive in terms of computational time.
Using QSE, Colless et al. demonstrated that they could calculate the excited states of H2 on a quantum computer comprised of two qubits. In their setup, each qubit was a superconducting transmon, which is a popular solid-state qubit option because of its relatively low sensitivity to stray charge. This microscopic device consists of a nonlinear inductor (typically, a Josephson junction) shunted by a capacitor, and it can be rotated between its two lowest energy states with microwave pulses. In each QSE calculation, the team assumed that the two hydrogen atoms in the molecule were separated by a fixed distance, and they mapped the Hamiltonian for this molecule onto the Hamiltonian of the two qubits. By repeating the computation for 45 different interatomic distances, they were able to reconstruct an energy curve for a given excited state.
In their study, Colless et al. uncovered another intriguing feature of the QSE approach: it can be used to obtain a better estimate of the ground-state energy compared to that found from VQE alone. The researchers view this finding as empirical evidence that running QSE mitigates the effect of certain errors on the calculation. If this claim survives further tests, QSE could prove critical to achieving useful computation with so-called prethreshold quantum devices, which do not support useful error correction. The researchers are working to better understand the source of the error mitigation, which could benefit the development of other types of variational quantum simulation algorithms.
Excited states are usually more entangled than their ground-state counterparts. Accordingly, classical approaches for simulating excited states are generally more expensive or less accurate than those used to predict ground states. Colless et al. have shown that it’s possible to extend a practical quantum algorithm such as VQE to the more complicated problem of determining the excited states of a many-body system without difficult modifications to the quantum circuit containing the qubits or a big increase in the number of qubit measurements. The accuracy and speed of this quantum calculation still trails that of classical methods. But expected improvements, such as increasing the quality of the qubits, should soon close this gap and establish quantum simulation as a tool that quantum chemists and materials scientists can use to tackle difficult simulation problems.
This research is published in Physical Review X.
References
- J. I. Colless, V. V. Ramasesh, D. Dahlen, M. S. Blok, M. E. Kimchi-Schwartz, J. R. McClean, J. Carter, W. A. de Jong, and I. Siddiqi, “Computation of Molecular Spectra on a Quantum Processor with an Error-Resilient Algorithm,” Phys. Rev. X 8, 011021 (2018).
- B. P. Lanyon et al., “Towards Quantum Chemistry on a Quantum Computer,” Nat. Chem. 2, 106 (2010).
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu, and D. Lu, “NMR Implementation of a Molecular Hydrogen Quantum Simulation with Adiabatic State Preparation,” Phys. Rev. Lett. 104, 030502 (2010).
- A. Peruzzo, J. R. McClean, P. Shadbolt, M. Yung, X. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien, “A Variational Eigenvalue Solver on a Photonic Quantum Processor,” Nat. Commun. 5, 4213 (2014).
- P. J. J. O’Malley et al., “Scalable Quantum Simulation of Molecular Energies,” Phys. Rev. X 6, 031007 (2016).
- A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. R. Chow, and J. M. Gambetta, “Hardware-Efficient Variational Quantum Eigensolver for Small Molecules and Quantum Magnets,” Nature 549, 242 (2017).
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter, and W. A. de Jong, “Hybrid Quantum-Classical Hierarchy for Mitigation of Decoherence and Determination of Excited States,” Phys. Rev. A 95, 042308 (2017).