Sharpening the Features of Optical Lattices

Bryce Gadway

Viewpoint

Sharpening the Features of Optical Lattices

Bryce Gadway

Department of Physics, University of Illinois at Urbana-Champaign, Urbana, IL 61801-3080, USA

February 20, 2018• Physics 11, 19

Lasers trap cold atoms in a lattice of potential barriers much narrower than the lasers’ wavelength.

Figure caption — **Figure 1:** Setup for the creation of subwavelength dark state optical lattices. Through quantum interference effects, a control laser field ( $Ω_{c}$ ) and a probe laser field ( $Ω_{p}$ ) create “dark” states in the atoms. The spatial distribution of the dark states generates a 1D array of 10-nm-wide potential barriers between which the atoms are trapped.

Ultracold atomic gases offer unique opportunities to study quantum matter in a pristine, well-controlled environment. One general method for controlling the atoms and their interactions is to trap them in a so-called optical lattice—a periodic optical potential created by interfering laser beams. Lasers can “sculpt” such potentials with a spatial resolution determined by the laser light’s wavelength, which is typically around several hundred nanometers. Optical potentials that vary on shorter length scales could allow researchers to probe so-far inaccessible regimes of atomic interactions, but the fundamental limits posed by light diffraction challenge the realization of subwavelength lattices. Now, Yang Wang from the Joint Quantum Institute in Maryland and co-workers have managed to overcome these diffraction limits [1], creating an optical lattice with features 50 times smaller than the wavelength of the light that creates the lattice. This approach could allow quantum simulators based on cold-atom lattices to tackle a broad range of quantum problems in physics and chemistry.

The physical mechanism underlying most optical lattices is the ac-Stark effect, in which laser light causes shifts in an atom’s ground-state energy. In the standing-wave pattern created from two or more laser beams, this ac-Stark shift will vary with position. Atoms thus experience a periodic potential and can get trapped in the potential’s minima. Since the ac-Stark shift is proportional to light intensity, diffraction limits the optical potential’s features—such as potential wells, barriers, or the spacing between lattice sites—to be larger than about half the laser wavelength.

Researchers have recently proposed several nonoptical methods for radically reducing lattice length scales. These methods are based on trapping atoms with the electromagnetic fields produced at the surface of nanostructured materials. For example, the magnetic field induced by nanoscale vortex patterns in thin-film superconductors [2] may create a trapping lattice with nanometer spacings. While promising, these approaches may be hampered by disorder in the material or interactions between the material’s surface and the atoms.

Other proposed methods instead rely on coupling light with the internal multilevel energy structure of the atoms. Several of these proposals are based on using atoms with multiple pseudospin ground states, which can form “dressed” states through their coupling with electromagnetic fields [3, 4]. Using an appropriate combination of lasers or microwave fields, one can generate a spatial modulation of the dressed states, and a corresponding dressed-state lattice potential, with subwavelength structure. Unfortunately, the lasers used to create the lattices in these schemes can lead to excessive heating of the atoms, causing them to escape the lattice.

In 2016, two groups [5, 6] proposed that these heating problems could be circumvented by creating “dark” dressed states, which cannot absorb or emit photons. Following these theoretical proposals, Wang and co-authors have been able to trap ultracold ytterbium atoms in a lattice potential with features much smaller than the wavelength.

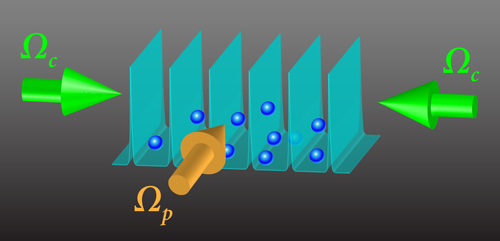
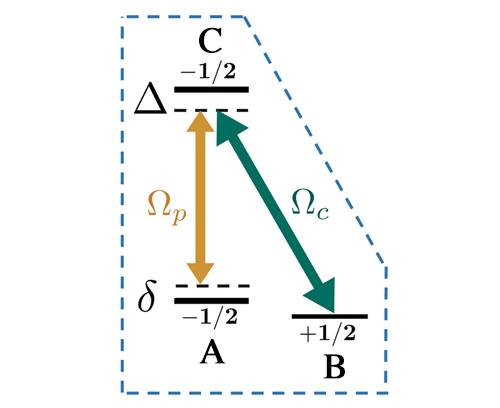
The new scheme uses a “control” laser field with amplitude $Ω_{c}$ and a “probe” laser field with amplitude $Ω_{p}$ (Fig. 1). The control field is generated by two counterpropagating circularly polarized laser beams, which interfere to create a standing wave. The weaker probe field, which has uniform amplitude, travels perpendicularly to the control beams. The control and probe fields couple two different hyperfine ground states of an atom (A and B, respectively) to one of the atom’s excited states (C). Together, the fields conspire to create a special dressed state that is a superposition of solely the two ground states (Fig. 2). A key feature of this dressed state is that it neither scatters nor absorbs light, because of destructive quantum interference between the transitions from the ground states to the excited state.

The nature of the dark states, that is, whether they look more like state A or state B, depends on the relative strengths of the control and probe fields and thus varies periodically in space, creating a spatially varying potential. As discussed in the 2016 proposals, the nonlinear response of the atoms amplifies the spatial modulations close to the nodes of the control field’s standing wave. This leads to a spikey potential lattice that can be described as a 1D array of delta-function-like barriers known as a Kronig-Penney potential. The barrier widths, which are determined solely by the amplitude ratio of the two fields ( $Ω_{p} ∕ Ω_{c}$ ), can be much smaller than the wavelength of the laser that creates the optical lattice.

The authors experimentally characterized the dark state optical lattice by measuring the lattice’s energy bands. To do so, they prepared the ytterbium atoms in the lowest-energy band of the dark state optical lattice. They then shook the lattice by modulating the frequency of one of the control-field laser beams, exciting some of the atoms to the higher-energy bands of the lattice and then measuring the resulting band populations through a technique known as band mapping. From the measured band energies, they confirmed that their dark state lattice was accurately described by a Kronig-Penney potential. The lattice featured 10-nm-wide barriers, roughly 50 times smaller than the wavelength of the employed lasers.

Even in this first demonstration of a dark state lattice, the measured lifetimes of the atoms in the lattice were relatively long. While the dressed states are created through quantum interferences involving the atoms’ excited states, the excited states are never populated, allowing the dark state lattice lifetime to be $1 0^{5}$ times longer than the excited-state lifetime. The authors expect that more intense lasers could lead to a further order-of-magnitude improvement in lifetime. Importantly, the lattice is much less sensitive to laser-intensity noise than conventional lattices because its shape depends only on the ratio of the control and probe fields. Hence, the two fields’ intensity fluctuations largely cancel out if the fields are generated from the same laser.

Results like those of Wang et al. point to a bright future for dark state potentials, whose applications could be manifold. The ability to trap atoms in a Kronig-Penney lattice offers exciting possibilities for studying many-body physics. For example, recent studies [7] suggest that atoms in excited bands of a Kronig-Penney lattice could form exotic superfluids that are stable enough to be studied. Furthermore, the nanometer-thin barriers could be useful for creating tunnel-junction elements in atomtronic circuits [8, 9]. But the most impactful implication could be the generation of lattices with subwavelength spacings. In conventional optical lattices, the wavelength-limited micrometer-scale lattice spacing means that the energy scales of the system—relevant for quantum phenomena ranging from tunneling to superexchange—are very low. The temperatures needed to access these energy scales present a challenge for current thermometry and cooling techniques. Subwavelength spacing could dramatically increase the system’s energy scales, allowing the study of many emergent quantum phenomena at achievable temperatures. A lattice with subwavelength spacings could be obtained, for instance, by dynamically shifting the position of a Kronig-Penney dark state lattice (with spacing $d = 𝜆 ∕ 2$ , where $𝜆$ is the light’s wavelength) by a fraction of that spacing ( $d ∕ N$ , where $N$ is an integer) [4]. The trapped atoms would experience an average potential with an effective spacing $d ∕ N$ , which could be made arbitrarily small.

This research is published in Physical Review Letters.

References

Y. Wang, S. Subhankar, P. Bienias, M. Łącki, T.-C. Tsui, M. A. Baranov, A. V. Gorshkov, P. Zoller, J. V. Porto, and S. L. Rolston, “Dark State Optical Lattice with a Subwavelength Spatial Structure,” Phys. Rev. Lett. 120, 083601 (2018).
O. Romero-Isart, C. Navau, A. Sanchez, P. Zoller, and J. I. Cirac, “Superconducting Vortex Lattices for Ultracold Atoms,” Phys. Rev. Lett. 111, 145304 (2013).
W. Yi, A. J. Daley, G. Pupillo, and P. Zoller, “State-Dependent, Addressable Subwavelength Lattices with Cold Atoms,” New J. Phys. 10, 073015 (2008).
S. Nascimbene, N. Goldman, N. R. Cooper, and J. Dalibard, “Dynamic Optical Lattices of Subwavelength Spacing for Ultracold Atoms,” Phys. Rev. Lett. 115, 140401 (2015).
F. Jendrzejewski, S. Eckel, T. G. Tiecke, G. Juzeliūnas, G. K. Campbell, L. Jiang, and A. V. Gorshkov, “Subwavelength-Width Optical Tunnel Junctions for Ultracold Atoms,” Phys. Rev. A 94, 063422 (2016).
M. Łącki, M. A. Baranov, H. Pichler, and P. Zoller, “Nanoscale ‘Dark State’ Optical Potentials for Cold Atoms,” Phys. Rev. Lett. 117, 233001 (2016).
A. Isacsson and S. M. Girvin, “Multiflavor Bosonic Hubbard Models in the First Excited Bloch Band of an Optical Lattice,” Phys. Rev. A 72, 053604 (2005); G. Wirth, M. Ölschläger, and A. Hemmerich, “Evidence for Orbital Superfluidity in the P-Band of a Bipartite Optical Square Lattice,” Nat. Phys. 7, 147 (2010).
C. Ryu, P. W. Blackburn, A. A. Blinova, and M. G. Boshier, “Experimental Realization of Josephson Junctions for an Atom SQUID,” Phys. Rev. Lett. 111, 205301 (2013).
S. Eckel, J. G. Lee, F. Jendrzejewski, N. Murray, C. W. Clark, C. J. Lobb, W. D. Phillips, M. Edwards, and G. K. Campbell, “Hysteresis in a Quantized Superfluid ‘Atomtronic’ Circuit,” Nature 506, 200 (2014).

About the Author

Bryce Gadway is an Assistant Professor of Physics at the University of Illinois at Urbana-Champaign. He is an experimentalist working in atomic, molecular, and optical physics, and he specializes in the use of ultracold atoms and molecules for quantum simulation and the exploration of new states of quantum matter. His group at the University of Illinois has made contributions to the study of topological and disordered systems using ultracold atoms, with the general aim of exploring novel transport phenomena driven by the marriage of these ingredients and interactions. In pursuit of these goals, his group has pioneered new techniques based on developing synthetic lattices for cold atoms and molecules.