A Toy Model for Active Interfaces
A deep concept in contemporary physics is universality, the idea that the behaviors of seemingly different systems are governed by the same underlying principles. Consider the edge of a drying coffee stain, the combustion front of a piece of burning paper, and the border of an expanding bacterial colony. Zoom out from the microscopic details and one finds that all three cases involve two media separated by a growing interface, whose essential features can be described by a simple equation [1] (see 18 January 2018 Focus story). This universality allows insights learned about one type of interface to be applied to another. But an open question is whether and how this universality extends to the fully nonequilibrium interfaces that prevail in biology, such as growing cellular membranes interacting with proteins. Francesco Cagnetta and colleagues at the University of Edinburgh, UK, have developed a simple and elegant model for a cellular membrane that captures some of this complexity [2]. The new model accounts for the bidirectional coupling between the membrane and embedded proteins, predicting the membrane’s dynamics in ways that might be relevant to cell motion and other biological processes.
The general equation that describes the drying coffee stain and other interface-growth phenomena is known as the Kardar-Parisi-Zhang (KPZ) equation [1]. It predicts the dynamics of an interface between two media when one medium “invades” the other, and it can be used to predict scaling laws, such as how the size of interface fluctuations varies with time or interface length. Fluctuations are deviations from a smooth interface, and these “bumps” and “valleys” tend to be much larger in KPZ interfaces than in stable interfaces. An extension of the KPZ model asks how “tracer” particles embedded within the interface would respond to such fluctuations [3]. Many proteins, for example, are narrower on one end than the other—a bit like a lampshade. The molecules therefore prefer to embed themselves in the curved regions of an interface [4], causing them to cluster into a membrane’s valleys.
Missing from this picture is the possibility that proteins or tracer particles exert a feedback on the membrane and thereby affect its shape. The membranes of red blood cells provide a case in point. Embedded proteins exert “active forces” on the cellular membrane as they convert chemical energy into mechanical work like the pumping of ions or the activation of tiny “molecular motors.” Even when a red blood cell’s membrane isn’t growing, these forces cause fluctuations in the membrane shape that have distinctive out-of-equilibrium properties. Models of the mutual feedback between proteins and shape in nongrowing membranes have predicted spatial patterning of the proteins or traveling waves in the membrane [4–8].
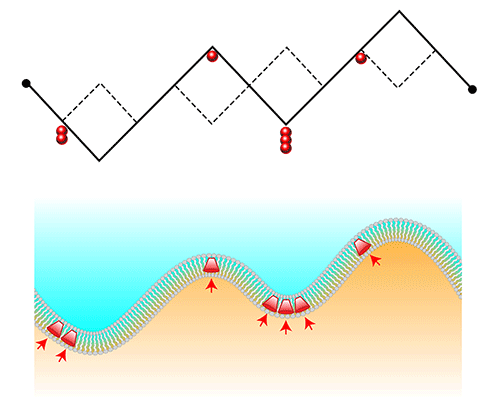
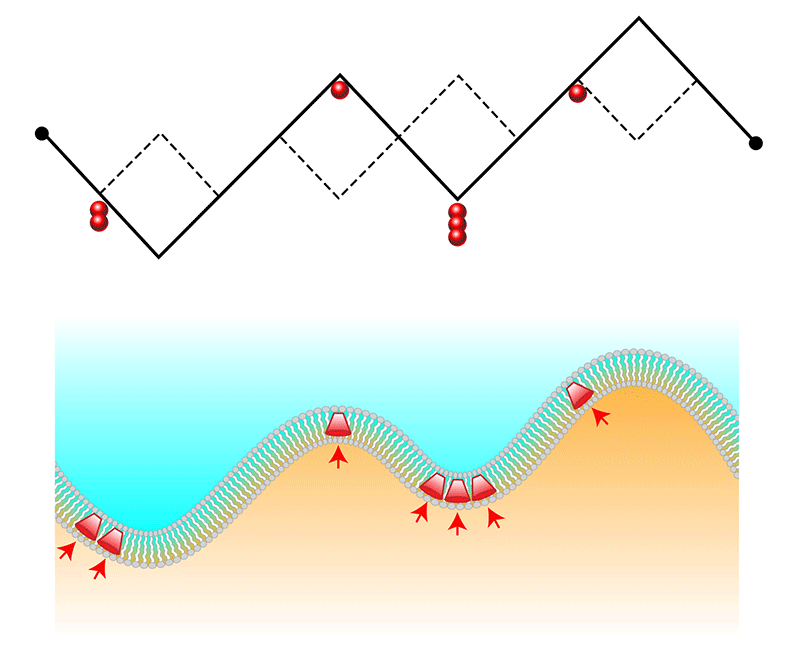
The model from Cagnetta and colleagues is of special interest because it combines two statistical physics problems—an actively growing membrane and the membrane-protein feedback—into one. Their model considers a membrane as a continuous 1D chain of slash-shaped links, which can point up (like a regular slash, ∕) or down (like a backslash, ∖) (Fig. 1). This chain could represent the advancing “footprint” of a cell migrating along a surface. To simulate active forces from embedded proteins, the model introduces particles that tend to accumulate in valley-shaped kinks. These proteins also stimulate upwards growth by “breaking” a valley and turning it into a crest.
The researchers’ numerical simulations of this model, which they back up with analytical predictions, reveal fluctuations that are neither describable by the KPZ equation nor by equilibrium models. One new behavior is the emergence of “microphase” separation, where proteins cluster at points along the chain but only up to a self-limiting cluster size. This finding could help to explain why the front interface of a migrating cell is often found to contain dynamic protein nanoclusters. A second manifestation of the coupling between the active particles and the interface curvature is the existence of shock waves. These waves are able to propagate along the interface because the proteins continually break the valleys in which they congregate. The propagating waves cause a corresponding oscillation in the interface “width,” which in a 1D chain is the average size of the chain’s fluctuations. Similar spatiotemporal dynamics have been observed in biological membranes [8], although determining whether this is indeed a result of the effects described by the model will require further experimental testing [4–9].
With the salient features of this new toy model understood, theorists will naturally want to tinker with it and see what happens. First up is likely an investigation into how the dynamics may change for a 2D chain and whether the model can be connected to other statistical-physics models. There will also be interest in exploring a more realistic type of force feedback between the proteins and the membrane shape. Cagnetta et al. intentionally chose a simple feedback to emphasize its effect on interfacial growth. But increasingly, researchers are working to derive physical descriptions of surfaces undergoing active biophysical or chemical processes. For example, studies have described the cell cytoskeleton in terms of various types of active gel and then explored the cytoskeleton’s effect on the lipid membrane to which it’s attached—an approach that has reproduced key properties of the cellular-tissue interface [7, 8, 10]. Integrating the new model with more realistic mechanical models will be a fascinating theoretical challenge, with broad applications in biology.
In cell biology, advances in microscopy, genetic manipulation, and image processing have made it possible to acquire complex and high-dimensional datasets. However, making sense of these datasets is hard because even a single biophysical phenomenon may involve interactions between many components (genes, proteins, membranes, and so on.) A theoretical model like that derived by Cagnetta and colleagues can be extremely helpful: it contains a reasonably complex feedback between its components yet can be used to derive simple and general scaling laws for observable quantities.
This research is published in Physical Review Letters.
References
- M. Kardar, G. Parisi, and Y.-C. Zhang, “Dynamic Scaling of Growing Interfaces,” Phys. Rev. Lett. 56, 889 (1986).
- F. Cagnetta, M. R. Evans, and D. Marenduzzo, “Active Growth and Pattern Formation in Membrane-Protein Systems,” Phys. Rev. Lett. 120, 258001 (2018).
- D. Das, M. Barma, and S. N. Majumdar, “Fluctuation-Dominated Phase Ordering Driven by Stochastically Evolving Surfaces: Depth Models and Sliding Particles,” Phys. Rev. E 64, 046126 (2001).
- S. Ramaswamy, J. Toner, and J. Prost, “Nonequilibrium Fluctuations, Traveling Waves, and Instabilities in Active Membranes,” Phys. Rev. Lett. 84, 3494 (2000).
- N. Gov, “Membrane Undulations Driven by Force Fluctuations of Active Proteins,” Phys. Rev. Lett. 93, 268104 (2004).
- J.-B. Manneville, P. Bassereau, D. Lévy, and J. Prost, “Activity of Transmembrane Proteins Induces Magnification of Shape Fluctuations of Lipid Membranes,” Phys. Rev. Lett. 82, 4356 (1999).
- H. Turlier, D. A. Fedosov, B. Audoly, T. Auth, N. S. Gov, C. Sykes, J.-F. Joanny, G. Gompper, and T. Betz, “Equilibrium Physics Breakdown Reveals the Active Nature of Red Blood Cell Flickering,” Nat. Phys. 12, 513 (2016).
- N. S. Gov, “Guided by Curvature: Shaping Cells by Coupling Curved Membrane Proteins and Cytoskeletal Forces,” Phil. Trans. R. Soc. B 373, 20170115 (2018).
- J. Allard and A. Mogilner, “Traveling Waves in Actin Dynamics and Cell Motility,” Curr. Opin. Cell Biol. 25, 107 (2013).
- G. Salbreux and F. Jülicher, “Mechanics of Active Surfaces,” Phys. Rev. E 96, 032404 (2017).