Jamming Grains Come Full Circle

Stefan Luding

Viewpoint

Jamming Grains Come Full Circle

Stefan Luding

University of Twente, Enschede, Netherlands

October 7, 2019• Physics 12, 109

The characterization of a new transition in sheared grains helps to fill in the phase diagram for granular materials.

Figure caption — **Figure 1:** A 2D granular system is placed under shear stress within a ring-shaped cell. The shear is generated by rotation of the outer wall, as well as independently moving concentric rings below the grains. The rotation rate (red arrows) increases with radius, resulting in a uniform shear. On the left, the grains are imaged in white light, while on the right, a polarized green light source is used to highlight grains that are experiencing strong contact forces.

The study of granular materials is important for a wide range of fields from industry to geophysics [1]. One of the unique aspects of grains is that they can behave like fluids or like solids—sometimes switching unpredictably between the two phases. For example, the grains stored in silos are supposed to flow out of and down chutes like a fluid, but too often solid-like arches clog the flow. On the other hand, dense packings of snow or soil can suddenly transform into a flowing avalanche or landslide. To probe these fluid-solid transitions Yiqiu Zhao from Duke University, North Carolina, and colleagues have designed a new “ring-shear” experiment that uses concentric rings to shear a 2D granular system of centimeter-wide disks [2]. The team used their data to construct a phase diagram, which reveals, for the first time, the transition between fragile solids with fluid-like features and shear-jammed solids that are stable against shear reversals. This fuller picture of granular transitions will be useful in developing better, more predictive models for understanding and avoiding grain-related problems and disasters.

Granular materials are unlike simple fluids or solids in that they are not fully described by basic macroscopic variables such as density, pressure, and temperature. This difference arises because granular materials have a microstructure—or “fabric”—that can change whenever they are disturbed [3, 4]. This microstructure evolution is evident in the history dependence of the isotropic jamming density $𝜑_{J}^{0}$ . Below $𝜑_{J}^{0}$ , a granular system behaves like a fluid, but when compressed to densities above $𝜑_{J}^{0}$ , the grains form strong force chains—linear paths of large contact forces—that give the material a solid-like internal structure. The way the system has been previously compressed determines the present chain configuration, and any new deformation can lead to a plastic, irreversible change of the fabric—mostly increasing $𝜑_{J}^{0}$ [3, 4]. As a result, the value of the jamming density is not fixed but varies according to the microstructure history [5].

To explore further the role of the microstructure’s evolution on the macroscopic granular behavior, researchers perform experiments in which a granular material is sheared. The traditional setup is two-dimensional, with the grains confined in a flat, annular (ring) shear cell, whose outer or inner cylindrical wall rotates [6, 7]. This rotation generates shear stresses that cause anisotropic, direction-dependent deformations and rearrangements of the microstructure. Unfortunately, the granular system typically splits up (bifurcates) into a solid-like region and a more fluid-like region, called a shear band. This dual-phase configuration prevents researchers from exploring the poorly understood intermediate states, which presumably will offer some insight into the microstructure rearrangements that drive fluid-solid transitions, as well as the steady-state flows [8].

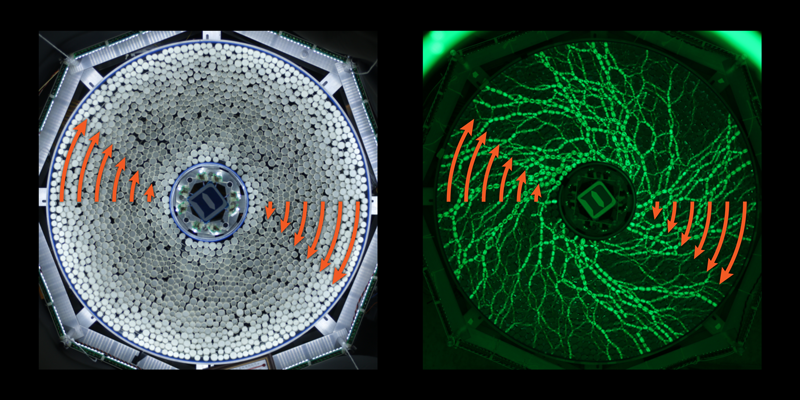
Zhao and colleagues were able to probe these intermediate states using a new experimental ring-shear-cell design [2]. Their device consists of concentric rings that rotate independently from the cell’s outer wall and from each other, producing an almost homogeneous shear profile—at least for grain densities that are not too large. This more uniform shear helps to monitor the force chains and other microstructure features in their system. As in previous work [6, 7, 9, 10], Zhao et al. used grains (disks) made of a photoelastic material whose stress-dependent light response can be used to distinguish which grains are experiencing large versus small contact forces (Fig. 1).

In their experiments, the team increased the shear amplitude (strain) and observed the onset of shear jamming [4, 9]. The shear jamming transition point $𝜑_{J}^{s h e a r}$ occurred at densities below the isotropic jamming density $𝜑_{J}^{0}$ . The reason for this lower density threshold is that sheared grains have a looser and more anisotropic configuration compared to compressed-only grains. The less-efficient packing results in a volume expansion (dilatancy) that is noticeable on the beach when the sand being sheared under our feet expands and becomes dry. However, in the confined space of the shear cell, the less-efficient packing leads to an increase of stress (pressure-dilatancy), which can cause shear jamming when the density is above $𝜑_{J}^{s h e a r}$ .

The team also looked at what happened when the shear was reversed. At shear reversal, the system is allowed to return to configurations that it had explored before. Changes in microstructure now must lead to a less anisotropic, more efficiently packed state. If this effect is large enough, unjamming happens after reversal, and the state is termed “fragile” (which differs from the traditional use of this term [9]). However, in other cases, the system remains jammed, and the state is labeled “shear jammed.” Zhao et al. found that—above a given shear strain and stress—certain minimum densities, $𝜑_{F}$ and $𝜑_{S J}$ , are required for the system to support fragile states or shear-jammed states, respectively. Unlike $𝜑_{J}^{0}$ , these transition densities are not history dependent, thus making it possible to pinpoint, for the first time experimentally, where fragile states and shear-jammed states exist in the granular material’s phase diagram and to observe the transitions between them.

The intermediate density $𝜑_{S J}$ is the most striking of the system’s transition points. When this density threshold is crossed, both the macroscopic state variables and the microscopic system descriptors (like the number of contacts per grain and the fabric anisotropy) are varying qualitatively. In my opinion, $𝜑_{S J}$ is special because it is where the solid-like features win against the fluid-like features [5]. Both below and above $𝜑_{S J}$ , one has a solid contact network (sustained by the frictional base), but the stability of this network changes from fluidly fragile to solidly shear jammed when one crosses the transition. Such an intermediate state has not been studied in any experiment to my knowledge. The new results allow us to identify an intermediate transition that is normally evaded by the system that bifurcates in a loose shear band and a dense solid. Further investigation of this region should offer insights into fluid-solid transitions, such as silo clogging and avalanches, where compression and shear effects are active at the same time.

This research is published in Physical Review Letters.

References

I. Einav and A. M. Puzrin, “Pressure-dependent elasticity and energy conservation in elastoplastic models for soils,” J. Geotech. Geoenviron. Eng. 130, 81 (2004); Q. Zhang and K. Kamrin, “Microscopic description of the granular fluidity field in nonlocal flow modeling,” Phys. Rev. Lett. 118, 058001 (2017).
Y. Zhao, J. Barés, H. Zheng, J. E. S. Socolar, and R. P. Behringer, “Shear-jammed, fragile, and steady states in homogeneously strained granular materials,” Phys. Rev. Lett. 123, 158001 (2019).
E. Andò, J. Dijkstra, E. Roubin, C. Dano, and E. Boller, “A peek into the origin of creep in sand,” Granul. Matter 21, 11 (2019); M. Wiebicke, E. Andò, V. Šmilauer, I. Herle, and G. Viggiani, “A benchmark strategy for the experimental measurement of contact fabric,” 21, 54 (2019).
N. Kumar and S. Luding, “Memory of jamming–multiscale models for soft and granular matter,” Granul. Matter 18, 1 (2016).
S. Luding, “So much for the jamming point,” Nat. Phys. 12, 531 (2016).
D. Howell, R. P. Behringer, and C. Veje, “Stress fluctuations in a 2D granular couette experiment: A continuous transition,” Phys. Rev. Lett. 82, 5241 (1999).
M. Lätzel, S. Luding, H. J. Herrmann, D. W. Howell, and R. P. Behringer, “Comparing simulation and experiment of a 2D granular Couette shear device,” Eur. Phys. J. E 11, 325 (2003).
A. Nicolas, E. E. Ferrero, K. Martens, and Jean-Louis Barrat, “Deformation and flow of amorphous solids: Insights from elastoplastic models,” Reviews of Modern Physics 90, 045006 (2018); M. M. Bandi, P. Das, O. Gendelman, H. G. E. Hentschel, and I. Procaccia, “Universal scaling laws for shear induced dilation in frictional granular media,” Granul. Matter 21, 40 (2019); Sudeshna Roy, Stefan Luding, and T. Weinhart, “A general(ized) local rheology for wet granular materials,” New J. Phys. 19, 043014 (2017).
D. Bi, J. Zhang, B. Chakraborty, and R. P. Behringer, “Jamming by shear,” Nature 480, 355 (2011).
D. M. Walker, A. Tordesillas, J. Ren, J. A. Dijksman, and R. P. Behringer, “Uncovering temporal transitions and self-organization during slow aging of dense granular media in the absence of shear bands,” Europhys. Lett. 107, 18005 (2014).

About the Author

Stefan Luding received his Ph.D. from the University of Freiburg, Germany. After a postdoc at Paris IV, Jussieu, he joined the Computational Physics group at the University of Stuttgart, Germany, where he achieved his habilitation in 1998. In 2001, he moved to DelftChemTech at Delft University of Technology, Netherlands, as Associate Professor in Particle Technology. Since 2007 he has chaired the group Multiscale Mechanics (MSM) at the Faculty of Engineering Technology and MESA+ at the University of Twente, Netherlands. His major research interests are granular matter, non-Newtonian flow rheology, nonlinear solids, particle interactions, cohesive powders, asphalt, composites, bio-/micro-fluid systems, self-healing materials, and micro-macro transition methods.