A Theory to Tackle Supercooling
Liquids are fascinating. As Feynman said in his famous lectures, watching a stream or waterfall, one has the impression that liquids are “almost alive relative to solids” [1]. Although the development of a theory for liquids trailed that for solids by several decades, modern theory can explain a rich variety of liquid behavior and properties. But a phenomenon that has proven difficult to treat theoretically is a supercooled liquid, the highly viscous state that can form when a liquid is cooled below its freezing point but doesn’t crystallize. A promising theoretical framework for tackling the supercooled state has now been proposed by Patrick Royall of the University of Bristol in the UK, Roland Roth of the University of Tübingen in Germany, and colleagues, who have developed a new method for calculating the structure of liquids on a microscopic level [2]. This approach, which assumes liquid particles congregate into multiparticle clusters, offers a way to test different supercooling theories.
Based on everyday experience, a liquid seems easy to distinguish from a solid. Liquids “flow,” sometimes developing eddies and swirls. And, if left alone, a liquid conforms to the shape of its container. Liquids and solids can be distinguished by their shear modulus, which characterizes a material’s stiffness and is nonzero for solids but vanishes for liquids. The distinction becomes even clearer on a microscopic level: the atoms or molecules in a liquid do not have fixed positions as they do in a solid but instead move around freely. Still, a liquid does have a microscopic structure in the sense that the positions of nearby particles are not completely independent of one another. This “correlation” occurs because the Pauli exclusion principle leads to an “excluded volume” around each particle. Nearby particles can’t enter this region, so they arrange in concentric, “fuzzy” shells that extend over a few particle widths beyond the excluded volume. Typically, physicists quantify these local arrangements through two-point correlations, which determine the probability of finding any two particles in a liquid at a given separation. This information can be measured by scattering x rays or neutrons from the liquid, and it forms the basis of a comprehensive statistical theory of the liquid state. This theory can be used to predict a liquid’s shear modulus or heat capacity, as well as phase transitions and critical phenomena [3].
However, conventional liquid-state theory loses its predictive power when describing a remarkable transition that can occur in cooled liquids. Most liquids, when cooled, reach a point where a crystalline phase is favorable. But virtually all liquids can be cooled beyond this point if the cooling is sufficiently fast, forming instead an amorphous solid, or “glass.” The constituent particles of a glass are disordered as in a liquid, but they cease to flow. Many theories for the glass transition have been put forward, but they all struggle to explain a basic observation: The viscosity at the transition increases by more than 10 orders of magnitude while the microscopic structure remains essentially unchanged, as evidenced by measurements of the two-point correlation function.
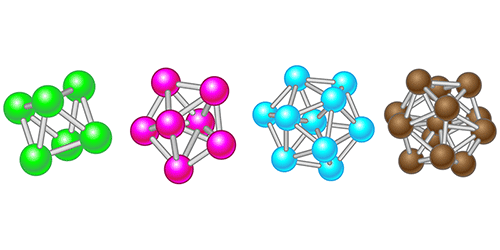
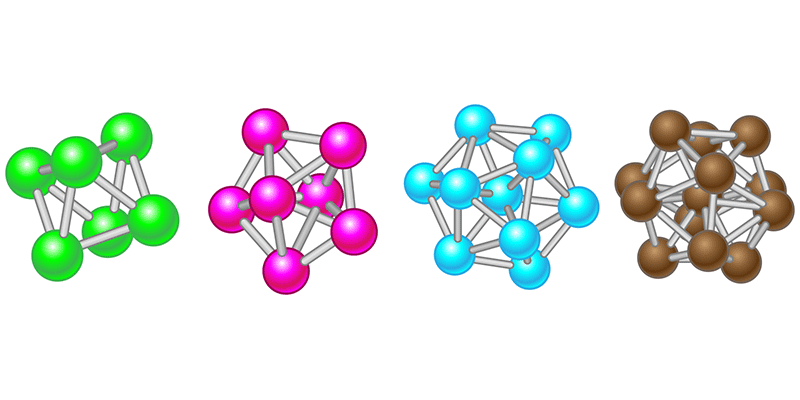
The reason might be that correlations between multiple particles have a significant effect on a supercooled liquid’s behavior, so two-point correlations are not providing enough information. Enter the work by Royall, Roth, and colleagues, who have devised an analytic framework to calculate many-particle correlations. The crux of their approach is to consider actual local arrangements of the particles (Fig. 1) that make up a liquid—an idea pioneered by crystallographer John Desmond Bernal in the late 1950s. Bernal believed one could model a liquid as a collection of hard spheres whose microscopic arrangements determine the liquid’s behavior [4]. Computers were still a novelty at the time, so he studied the properties of random packings of spheres by assembling models in his office (Fig. 2).
The team builds on Bernal’s approach by visualizing a liquid as a collection of local, ever-rearranging clusters of a few particles interacting through the excluded volume effect. They then focus on a specific cluster—say one made up of five particles. Assuming the cluster is fixed in a “sea” of surrounding particles, they calculate its free energy, which determines the probability of encountering the cluster in the liquid. An essential tool that makes these calculations feasible is a type of geometry-based mathematics [5] in combination with ideas from classical density-functional theory for inhomogeneous liquids [6].
Such free-energy calculations of clusters are important for the following reason: In order for a liquid to evolve in time, the clusters have to transform, which can be pictured as a journey through a high-dimensional, rugged energy landscape. In a normal liquid, the free-energy barriers between local structures are small enough to allow particles to move freely. But these barriers become high in a supercooled liquid, which is why flow becomes so slow. The new theory opens the door to calculating the height of these local barriers and therefore the cluster transition rates that govern the viscosity of the liquid. This can potentially be exploited to rigorously test complementary theories of the glass transition such as the popular random first-order transition theory [7, 8].
In a demonstration of their approach, the researchers considered a hard-sphere liquid and studied a range of “reference” cluster types [9] with up to 13 particles (enough to describe a particle and the first fuzzy shell around it). A 2012 experimental and simulation study of a hard-sphere liquid related some of the same clusters to the emergence of slow dynamics and freezing [10]. Thanks to the new approach, there is now a theoretical basis for predicting the frequency and dynamics of such clusters in a liquid.
The study of slow dynamics, as in supercooled liquids, has long been dominated by computer simulations. The work from Royall, Roth, and colleagues may give analytical theory a chance to catch up and provide fresh insight and quantitative predictions for supercooled liquids. Ultimately, the goal is to discriminate between the many competing explanations for the supercooled state in order to have a single, comprehensive theoretical picture. The new approach could help physicists do this—and potentially much more. One application would be describing the formation of molecules and other structures that self-assemble in solutions of multicomponent building blocks [11]. Eventually, the framework could help enable a first-principles prediction of the way a protein will fold based on the molecule’s genetic code.
This research is published in Physical Review Letters.
References
- R. Feynman, The Feynman Lectures on Physics (The Perseus Books Group, New York, 2011)[Amazon][WorldCat].
- J. F. Robinson, F. Turci, R. Roth, and C. P. Royall, “Morphometric approach to many-body correlations in hard spheres,” Phys. Rev. Lett. 122, 068004 (2019).
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids (Academic Press, Amsterdam, 2006)[Amazon][WorldCat].
- J. L. Finney, “Bernal’s road to random packing and the structure of liquids,” Philos. Mag. 93, 3940 (2013).
- P.-M. König, R. Roth, and K. R. Mecke, “Morphological thermodynamics of fluids: Shape dependence of free energies,” Phys. Rev. Lett. 93, 160601 (2004).
- R. Evans, “The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids,” Adv. Phys. 28, 143 (1979).
- J.-P. Bouchaud and G. Biroli, “On the Adam-Gibbs-Kirkpatrick-Thirumalai-Wolynes scenario for the viscosity increase in glasses,” J. Chem. Phys. 121, 7347 (2004).
- V. Lubchenko and P. G. Wolynes, “Theory of structural glasses and supercooled liquids,” Annu. Rev. Phys. Chem. 58, 235 (2007).
- J. P. K. Doye, D. J. Wales, and R. S. Berry, “The effect of the range of the potential on the structures of clusters,” J. Chem. Phys. 103, 4234 (1995).
- J. Taffs, S. R. Williams, H. Tanaka, and C. P. Royall, “Structure and kinetics in the freezing of nearly hard spheres,” Soft Matter 9, 297 (2013).
- P. F. Damasceno, M. Engel, and S. C. Glotzer, “Predictive self-assembly of polyhedra into complex structures,” Science 337, 453 (2012).