Constructing Field Theories Using Quantum Simulators
One of the greatest challenges in physics is to understand how collective, macroscopic behaviors, such as phase transitions, emerge from the microscopic dynamics of the constituents of a system. A pivotal approach to tackle such many-body problems is offered by quantum field theory (QFT), which plays a central role in describing, for instance, superconductivity and the quantum Hall effect. QFT makes a number of problems solvable by describing a system in terms of fields distributed in space and time, while neglecting many of the microscopic details of the system. However, when developing a QFT description for a given system, it can be challenging to derive the theory’s parameters from experiments, limiting the theory’s predictive power. Now, Torsten Zache of Heidelberg University, Germany, and colleagues have demonstrated a new approach to incorporate experimental data into the construction of a QFT [1]. They show that the key building blocks for QFT can be derived from measurable correlation functions. They then provide an experimental validation of the approach using a quantum simulator. The result could allow researchers to use experiments to refine or develop QFTs for a broad range of experimental systems.
A striking outcome of applying a statistical approach to many-body systems is the notion of universality: A single theory can explain phenomena that may seem to be unrelated, like liquid-to-gas phase transitions and ferromagnetism [2]. This approach works because a system’s observable properties are often insensitive to the details of its microscopic constituents. The magnetization of a solid, for instance, may not depend on whether the magnetic moments of atoms in the lattice interact only with their nearest neighbors or with the third, fourth, or hundredth neighbor (as long as the interaction range is not infinite).
Quantum field theories are based on the same idea. In order to describe some phenomenon, we build the simplest theory that contains the essential ingredients of the system we want to study, without worrying about the details of the microscopic interactions. The theory obtained this way is thus universal and generally solvable (at least numerically) and depends on a set of parameters that can be derived by fitting experimental data. The problem is that one typically needs as many observables as QFT parameters. In practice, however, experiments provide a limited number of observables. This limits the number of free QFT parameters that can be derived from fitting and thus the flexibility to improve the QFT description of a given system.
For this reason, researchers may opt to solve the microscopic dynamics of a system exactly, instead of using QFT. In cases where no analytical solution exists, the rapidly advancing field of quantum simulation can help. The idea is to build and measure another system that is governed by the same model that we believe to describe the system of interest. If this “simulator” is sufficiently controlled and isolated, and if the measurements are sufficiently precise, its observed dynamics are, by construction, those of the initial system, which can be checked by comparing the behavior of the two systems. Today, such an approach is being applied in many laboratories using ultracold atoms, quantum optical setups, or superconducting circuits [3–5]. But while quantum simulation gives a “brute force” solution to one specific problem, it doesn’t have the general applicability of QFT.
Now, Zache and his co-workers have unveiled a powerful way to combine QFT and quantum simulation. They show that quantum simulator experiments can be used to directly determine the building blocks of a field theory. The authors’ approach is based on a special formulation of QFT using so-called equal-time phase correlation functions. Such correlations measure the probability that the field phases at two points differ by a certain amount at a given time. Using a Feynman diagram representation, the researchers show that these phase correlations are related to elementary bricks in the diagrams, called irreducible vertices. These vertices represent the key building blocks from which all physical observables may be derived. Considering a given field theory with a large number of parameters, the researchers demonstrate that these irreducible vertices can be expressed as a function of the parameters of the field theory. In other words, this result establishes a direct relationship between the QFT parameters and measurable correlation functions.
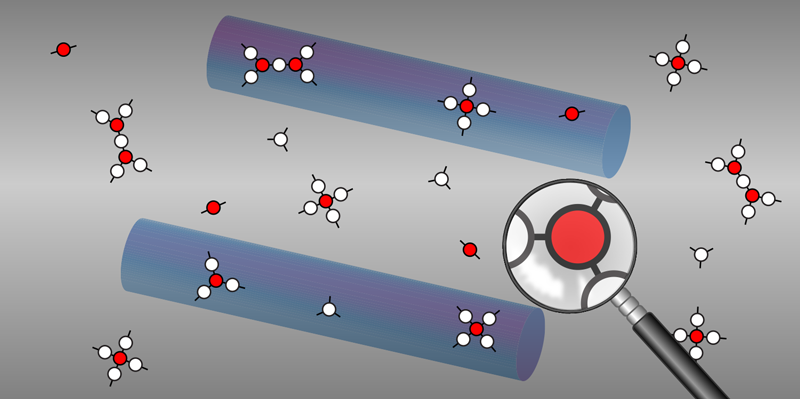
The authors provide a proof-of-principle experimental demonstration of their approach using a previously demonstrated experimental quantum simulator [6] of the sine-Gordon model. This model represents the field theory of quantum particles interacting in a periodic potential—such as electrons in a solid. The quantum simulator consists of two one-dimensional superfluids (Fig. 1). They prepare the superfluids by cooling rubidium atoms down to a few tens of nanokelvins and by trapping them with magnetic fields on an atom chip. The two parallel traps are separated by a barrier that can be adjusted to tune the probability that matter waves in one superfluid will tunnel into the neighboring superfluid.
Using matter-wave interferometry, the researchers measure the phase correlation functions inside the superfluids with great precision. These data are then used to determine the effective parameters of the field theory using the approach described above. They compare the derived parameters with those obtained by numerical calculations—which are doable for this simple sine-Gordon model in the regime of the experiments, where the quantum correlations between the particles are weak. The excellent agreement between calculated and measured parameters provides a compelling validation of the approach.
This successful benchmark now paves the way to studying more complex cases. Future work might attempt to solve sine-Gordon models in the regime of strong quantum correlations; improve the description of the superfluid-insulator transition, for which recent experiments revealed that the QFT parameters need to be revised [7]; and tackle nonequilibrium problems [8]. More generally, this work shows a new benefit of quantum simulators: Instead of just finding the physical behavior of a specific model, they can now be used to build and refine field theories that may be applicable not only to the system considered by the authors but also to a whole spectrum of many-body problems.
This research is published in Physical Review X.
References
- T. V. Zache et al., “Extracting the field theory description of a quantum many-body system from experimental data,” Phys. Rev. X 10, 011020 (2020).
- L. D. Landau et al., Statistical Physics, Part 1 (Elsevier, Oxford, 1980)[Amazon][WorldCat]; Statistical Physics: Theory of the Condensed State, Part 2 (Elsevier, Oxford, 1980)[Amazon][WorldCat].
- A. Trabesinger, “Quantum simulation,” Nat. Phys. 8, 263 (2012).
- L. Sanchez-Palencia, “Quantum simulation: From basic principles to applications,” C.R. Phys. 19, 357 (2018).
- J. Ignacio Cirac and P. Zoller, “Goals and opportunities in quantum simulation,” Nat. Phys. 8, 264 (2012).
- T. Schweigler et al., “Experimental characterization of a quantum many-body system via higher-order correlations,” Nature 545, 323 (2017).
- G. Boéris et al., “Mott transition for strongly interacting one-dimensional bosons in a shallow periodic potential,” Phys. Rev. A 93, 011601 (2016).
- M. Prüfer et al., “Experimental extraction of the quantum effective action for a non-equilibrium many-body system,” arXiv:1909.05120.