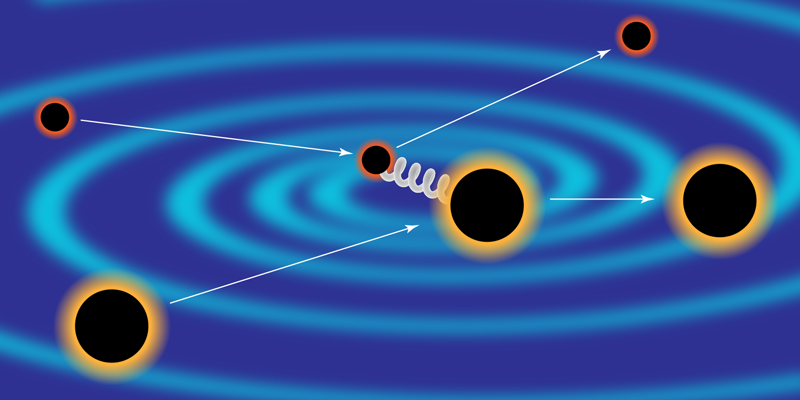
A High-Energy Take on Black Hole Encounters
Gravitational-wave astronomy sounds like science fiction: two massive black holes swirl toward each other at a substantial fraction of the speed of light, radiating a burst of energy that outweighs the Sun in the form of gravitational waves. Millions of light years away, on Earth, we observe these ripples in the geometry of spacetime through the tiny deformations they produce in kilometers-long arms of laser interferometers [1]. One crucial ingredient in interpreting these gravitational-wave signals is having accurate theoretical predictions for the observed waveforms, obtained through the notoriously difficult task of solving Einstein’s field equations. Future progress depends upon significantly improving these theoretical calculations, as current predictions may not be accurate enough for upgraded detectors coming online in 2022 [2]. Inspired by particle physics, where everything is conceptually reduced to scattering processes between point particles, some theorists have begun to attack the binary black hole problem by studying a related problem in which two black holes fly near each other and are deflected (scattered) by their gravitational interaction. Within this framework, Thibault Damour from the Institut des Hautes Études Scientifiques (IHES) in France and colleagues have sparked unanticipated progress in theoretical gravitational-wave predictions [3–5]. Their latest work shows that there exists a computational shortcut for the generic scattering problem by considering a special limit where one black hole weighs much less than the other.
The detection of gravitational waves—as well as the extraction of source information (such as mass, spin, and location) and the testing of fundamental physics—relies heavily on accurate theoretical models used as templates in the data analysis. Both sophisticated numerical simulations and perturbative analytic calculations are necessary for this purpose, and both need to improve in accuracy in order to analyze the data that will come from recently enhanced observatories (LIGO, Virgo, and KAGRA) and future instruments (LISA, Cosmic Explorer, and the Einstein Telescope) [2].
In perturbation theory, the equations of motion are written as a series of terms that contain some small quantity 𝜖 taken to increasing powers: first order 𝜖, second order 𝜖2, third order 𝜖3, etc. The landscape of perturbative analytic methods can be charted according to the quantity that is small: a weak gravitational field (the post-Minkowskian expansion), a weak field and slow-moving black holes (the post-Newtonian expansion), or a small mass ratio between the black holes (as in the gravitational self-force program). In the past, the post-Minkowskian approximation has received the least attention since it is most useful for the scattering of black holes—an event that would normally produce too little gravitational radiation to be observed. However, theorists recently realized that calculations made for scattering (unbound) black holes can reveal important elements, such as the gravitational potential, for merging (bound) systems. This connection has brought together researchers from the classical and quantum gravity communities, with a continuing interchange of fruitful ideas.
The basic idea in this scattering approach is to treat black holes as quantum particles that interact through the exchange of gravitons, in the same way that electrons interact through the exchange of photons (Fig. 1). By combining all the different ways that particles interact, researchers can achieve extremely precise predictions—as evidenced by the experimental confirmation of up to 12 digits of the predicted anomalous magnetic dipole moment of the electron [6]. A seminal quantum idea is that scattering amplitudes, which give the probability for particular scattering processes, are strongly constrained from general principles (symmetries, locality, conservation of probability). Several groups are currently applying these and other powerful techniques from quantum field theory to determine gravitational scattering amplitudes between “black hole particles.” The amplitudes are quantum observables, but researchers can extract a classical part, which can be used to construct templates for gravitational-wave analysis [7].
Damour has discovered a simple yet far-reaching connection between different perturbative approaches to classical black hole scattering calculations [3]. He has shown that the mass dependence of the classical scattering-angle function is such that the function can be completely fixed at a certain order in the post-Minkowskian approximation from lower orders in the self-force (small-mass-ratio) approximation. This finding is powerful since the latter approximation makes full use of the exact (nonlinear) black hole solutions in Einstein’s classical gravity. For instance, according to Damour’s findings, the fourth order in the post-Minkowskian approximation—one order above the state-of-the-art quantum amplitude calculation achieved by Zvi Bern and collaborators [7]—could be determined from only the first-order self-force calculations. This shortcut could accelerate efforts to reach higher-order (more accurate) predictions in the future. Already, Damour and his colleagues have used first-order self-force calculations to determine large parts of the fifth- to sixth-order post-Newtonian conservative dynamics, which are needed to pin down the gravitational potential in bound systems [4, 5, 8]. Some of the terms in these calculations have been fiercely debated and were the subject of a friendly wager between Bern and Damour [9], recently conceded by Damour [5].
While pushing forward on high-order perturbative predictions is certainly important, Damour has also challenged the community by raising issues over the fundamental aspects of quantum gravitational scattering research [3]. He has posed several subtle questions: Does it make sense to identify a classical part of a scattering amplitude, which is normally a probabilistic quantum observable with no direct classical analog? How precisely does the exchange of gravitons add up to large classical deflection angles? How does classical black hole scattering in the high-energy limit relate to quantum results for scattering of massless particles [10, 11]? Resolving these issues could help researchers map out future avenues to take toward more accurate predictions.
The study of scattering black holes has become a promising research direction, attracting diverse groups working within a vast range of methodologies. The latest efforts [3–5, 7, 8, 12] demonstrate the potential of this approach for gravitational-wave science: More accurate predictions at high orders in perturbation theory are coming within reach, and further progress in this area can greatly enhance the science capability of near-future gravitational-wave observatories. Furthermore, the confrontation of different communities and their ways of thinking bears unforeseeable opportunities for theoretical discoveries, even beyond gravitational waves. The time has come to pass this horizon.
This research is published in Physical Review D.
References
- B. P. Abbott et al. (LIGO Scientific and Virgo Collaborations), “Observation of gravitational waves from a binary black hole merger,” Phys. Rev. Lett. 116, 061102 (2016).
- M. Pürrer and C.-J. Haster, “Gravitational waveform accuracy requirements for future ground-based detectors,” Phys. Rev. Research 2, 023151 (2020).
- T. Damour, “Classical and quantum scattering in post-Minkowskian gravity,” Phys. Rev. D 102, 024060 (2020).
- D. Bini et al., “Binary dynamics at the fifth and fifth-and-a-half post-Newtonian orders,” Phys. Rev. D 102, 024062 (2020).
- D. Bini et al., “Sixth post-Newtonian local-in-time dynamics of binary systems,” Phys. Rev. D 102, 024061 (2020).
- T. Aoyama et al., “Tenth-order QED contribution to the electron g−2 and an improved value of the fine structure constant,” Phys. Rev. Lett. 109, 111807 (2012).
- Z. Bern et al., “Scattering amplitudes and the conservative Hamiltonian for binary systems at third post-Minkowskian order,” Phys. Rev. Lett. 122, 201603 (2019).
- D. Bini et al., “Novel approach to binary dynamics: Application to the fifth post-Newtonian level,” Phys. Rev. Lett. 123, 231104 (2019).
- Z. Bern, QCD Meets Gravity 2019 conference, introductory slides.
- D. Amati et al., “Higher-order gravitational deflection and soft bremsstrahlung in planckian energy superstring collisions,” Nucl. Phys. B 347, 550 (1990).
- Z. Bern et al., “Universality in the classical limit of massless gravitational scattering,” arXiv:2002.02459.
- A. Antonelli et al., “Gravitational spin-orbit coupling through third-subleading post-Newtonian order: From first-order self-force to arbitrary mass ratios,” Phys. Rev. Lett. 125, 011103 (2020).