Riding Waves in Neuromorphic Computing
Machine learning has emerged as an exceptional computational tool with applications in science, engineering, and beyond. Artificial neural networks in particular are adept at learning from data to perform regression, classification, prediction, and generation. However, optimizing a neural network is an energy-consuming process that requires a lot of computational resources. One of the ways to improve the efficiency of neural networks is to mimic biological nervous systems that utilize spiking potentials and waves—as opposed to digital bits—to process information. This so-called neuromorphic computing is currently being developed for intelligent and energy-efficient devices, such as autonomous robots and self-driving cars. In a new development, Giulia Marcucci and colleagues from the Sapienza University of Rome have analyzed the potential of using nonlinear waves—such as rogue waves and solitons—for neuromorphic computing [1]. These waves interact with each other in complex ways, making them inherently suited for designing neural network architectures. The researchers consider ways to encode information on the waves, providing recipes that could guide the development of machine-learning devices that can take advantage of wave dynamics.
A necessary neural network ingredient is complexity, which allows the system to approximate a given function or learn from a dataset. An example of this complexity is how a deep feed-forward network processes information. It consists of an input layer, hidden layers, and an output layer. From the input to output layers, information propagates through a complex system of hidden “neurons,” which are fully or partially connected to each other. The connections between neurons are characterized by parameters, or “weights.” The neurons perform linear and nonlinear transformations yielding a nonlinear mapping between the input and output. Optimizing the network consists of feeding it a training dataset and tuning the weights to arrive at a desired relationship between inputs and outputs. The nonlinearity in the information processing is a necessary condition for the network to become a universal approximator, which means it can represent any function when given appropriate weights.
An avenue for improving the efficiency of neural networks is to adopt neuromorphic techniques, which can provide extremely fast real-time computing at a low energy cost. Recent work has demonstrated neuromorphic computing in deep (multilayered) networks with representative platforms that include coherent nanophotonic circuits [2], spiking neurons [3], and waves [4]. But an open problem in neuromorphic computing of deep networks is the optimization of the parameters. Deep networks require many connections to be sufficiently complex; thus the training usually requires a lot of computational power. To reduce these computing demands, researchers have suggested alternative architectures, such as reservoir computing (RC) [5]. The input and hidden nodes in an RC network are randomly initialized and fixed, while only the weights of the output layer need to be trained. This approach makes the optimization more efficient than regular architectures, yet the network retains the requirements for learning complexity. Proposed designs for RC neuromorphic devices involve optoelectronic technology [6], photonic cavities [7], and photonic integrated circuits [8].
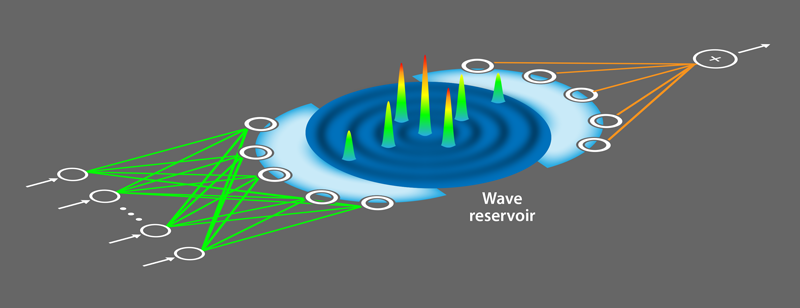
Marcucci and colleagues have now added to this list of potential RC neuromorphic devices with their proposed architecture based on wave dynamics [1]. They show the possibility of building a device that is able to learn by harvesting nonlinear waves. Nonlinear waves, such as solitons, breathers, and rogue waves, show divergent behavior and provide sufficient complexity to develop a learning method. The proposed architecture, called single wave-layer feed-forward network (SWFN), goes beyond standard neuromorphic RC because the reservoir comprises nonlinear waves rather than using randomly connected hidden nodes. In other words, the coupled artificial hidden neurons have been replaced by waves that interact naturally through interference. The SWFN architecture consists of three layers (Fig. 1): the encoding layer, where an input vector is written into the initial amplitude or phase of a set of representative waves; the wave reservoir layer, where the initial state evolves following a nonlinear wave equation; and the readout layer, where the output is recovered from the final state of the waves. As this network is an RC one, only the weights in the readout layer need to be trained.
Although wave dynamics have been used in neuromorphic computing [4, 7], a general theory that links nonlinear waves with machine learning was missing. Marcucci and co-workers introduced a general and rigorous formulation, bridging the gap between the two concepts. For their model system, the researchers encoded the input vector in the initial state of a set of plane waves and represented the wave evolution in the reservoir layer with the nonlinear Schrödinger equation—but any nonlinear wave differential equation would have worked. In fact, any system that is characterized by nonlinear wave dynamics can be used to build a neuromorphic nonlinear wave device. A simple example would be a wave tank with several wave generators on one end and wave detectors on the other.
From their general analysis, the researchers showed that two conditions must be fulfilled for a transition to the learning regime. First, the wave evolution must be nonlinear, as linear evolution would prevent the SWFN from being a universal approximator. The second condition connects the number of output channels with the size of the training data. Specifically, the number of output nodes has to be the same as the number of training data points per input node for the SWFN to approximate a function or to learn a finite dataset.
Marcucci and colleagues present three different encoding methods through three representative examples. First, the SWFN is used to approximate a one-dimensional function that maps a binary string to the initial phase of a set of waves. In the second example, the neuromorphic device is asked to learn an eight-dimensional dataset that is encoded in the initial amplitudes of the waves. In the last example, the researchers show that the proposed neuromorphic architecture can be used as Boolean logic gates that operate on two binary inputs. In each case, the SWFN performs as well as conventional neural networks verifying that SWFN is indeed a universal approximator able to approximate arbitrary functions and learn high-dimensional datasets.
Neural network technology is a rapidly growing scientific field, and neuromorphic computing can offer an energy-efficient way to meet the technology’s computing demands. Marcucci and colleagues have provided a recipe for a neuromorphic neural network using nonlinear wave dynamics. This groundwork opens the door to a wide range of nonlinear-wave phenomena in electronics, polaritonics, photonics, plasmonics, spintronics, hydrodynamics, Bose-Einstein condensates, and more. Among these wave-based technologies, photonics seems very promising, as photonic materials absorb little energy and can be fashioned into circuit elements at micro- or nanoscales. The computing in a photonic neural network is as fast as the speed of light, and different signals can be encoded in different frequencies, allowing multiple computations to be performed simultaneously. With such potential, it’s easy to imagine neuromorphic devices riding these waves to technological and engineering achievements in the near future.
References
- G. Marcucci et al., “Theory of neuromorphic computing by waves: Machine learning by rogue waves, dispersive shocks, and solitons,” Phys. Rev. Lett. 125, 093901 (2020).
- Y. Shen et al., “Deep learning with coherent nanophotonic circuits,” Nat. Photon. 11, 441 (2017).
- S. K. Esser et al., “Convolutional networks for fast, energy-efficient neuromorphic computing,” Proc. Natl. Acad. Sci. U.S.A. 113, 11441 (2016).
- T. W. Hughes et al., “Wave physics as an analog recurrent neural network,” Sci. Adv. 5, 6946 (2019).
- H. Jaeger and H. Haas, “Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication,” Science 304, 78 (2004).
- L. Larger et al., “High-speed photonic reservoir computing using a time-delay-based architecture: Million words per second classification,” Phys. Rev. X 7, 011015 (2017).
- S. Sunada and A. Uchida, “Photonic reservoir computing based on nonlinear wave dynamics at microscale,” Sci. Rep. 9, 19078 (2019).
- A. Katumba et al., “Low-loss photonic reservoir computing with multimode photonic integrated circuits,” Sci. Rep. 8, 2653 (2018).