How Laggards Help Decision-Making
When a new technology, such as the electric car, comes to market, consumers have to decide if they are going to adopt the innovation, and if so, which of the different brands and models to choose. Typically, decision-makers fall into “early adopter” and “laggard” categories [1], according to their propensity to innovate. Previous models have investigated different influences on decision-making [2] but have generally neglected how individuals consider the decisions of others in making up their own minds. Now Bhargav Karamched of Florida State University and colleagues have developed a model in which laggards evaluate an innovation by accounting for early adopters’ decisions [3]. The researchers find that laggards can help the group as a whole to reach a more beneficial decision without slowing down the decision-making process.
Over the past few years, techniques from statistical physics have helped researchers develop sociophysics models describing complex systems made of interacting agents. These models have shed light, for instance, on the dynamics of opinions within human societies [4] and on the evolution of languages and dialects [5]. A central component of all these models is the random walk—a path resulting from a series of random steps. In decision-making models, the random walk is performed by a parameter ( y) quantifying how an individual agent is disposed toward a particular opinion or behavior. y can go up or down as the agent gathers information. In assessing electric vehicles, for example, the environmentally friendly attitude of an agent might push y up, whereas the thriftiness of another agent would pull y down.
In a wealthy and environmentally conscious society, y will increase over time for most agents, driving a majority of the population to favor a decision that maximizes societal benefits—adopting electric cars. However, individual decisions are unpredictable: they can depend on an agent’s state of mind on a particular day. Therefore, y follows a “biased” random walk: as it evolves toward the socially responsible outcome, it doesn’t march straight toward it but fluctuates along the way. Determining if and when this stochastic process reaches a certain threshold—triggering a decision to buy an electric car—is a so-called first-passage problem [6].
Traditional sociophysics tackles decision-making processes by describing the evolution of beliefs with rules derived by fitting empirical data or by appealing to phenomenological principles [2, 4]. These approaches have successfully reproduced some features of collective decisions but cannot account for many psychological aspects that are relevant to these processes. Karamched and colleagues apply a model grounded in Bayesian statistics to describe how decisions by small groups of agents can offer information to the rest of the population that is still undecided [7]. Bayesian statistics is a mathematical framework often applied to processes in which the probability of an event depends on prior beliefs or knowledge related to the event. There is evidence that human reasoning and decision-making can be modeled as Bayesian inference, which, in turn, has facilitated the development of artificial-intelligence algorithms that mimic cognitive functions associated with the human mind [8].
Karamched and colleagues show that the accumulation of private information corresponds to a random walk driven by a constant force that drives each individual’s y in the direction of the outcome that would be favored by the majority of individuals. In their model, an agent makes their decision once the belief is sufficiently strong: if y reaches a threshold value +𝜃, the agent commits to the favorable option; if instead it hits −𝜃, the agent opts for the less favorable outcome. The value of 𝜃 depends on an agent’s personality: it’s small for an early adopter and large for a laggard.
Initially, all agents are undecided, with a random distribution of opinions ( y’s) that will slowly become skewed toward the favorable decision because of individual research. But when the first agent makes a decision, the rest of the group sees this decision. In the researchers’ model, observers react by adjusting their own y exactly by the threshold value of the decider ( +𝜃 or −𝜃), depending on which decision was made. What happens next depends on whether the population is homogeneous (all agents have the same threshold) or heterogeneous (there is a mix of early adopters and laggards with different thresholds).
For a homogeneous society, if the first decider goes for the favorable option, it will persuade any agent with a positive y to make the same decision. Because of the drift toward the favorable decision, a little over half the population falls into this category, which will persuade the remaining agents that the first decision was a good one. On the other hand, if the first decision is unfavorable, the agents with negative y will follow the leader, but they will account for slightly less than half the population. With that information, the undecided agents can infer that the first decision was unfavorable and pick the favorable one. Despite the poor initial decision, a slight majority will pick the most beneficial option.
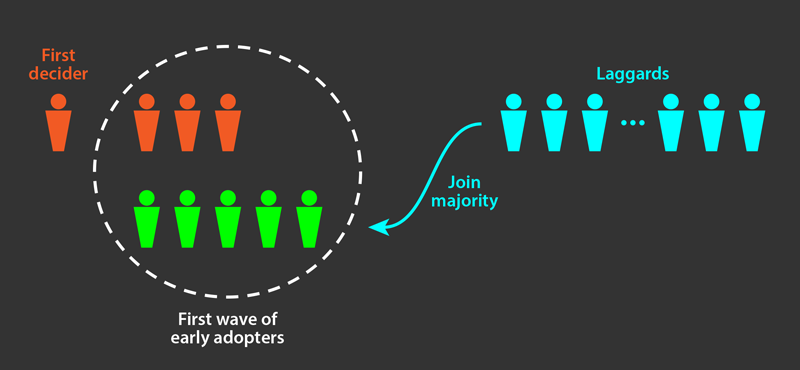
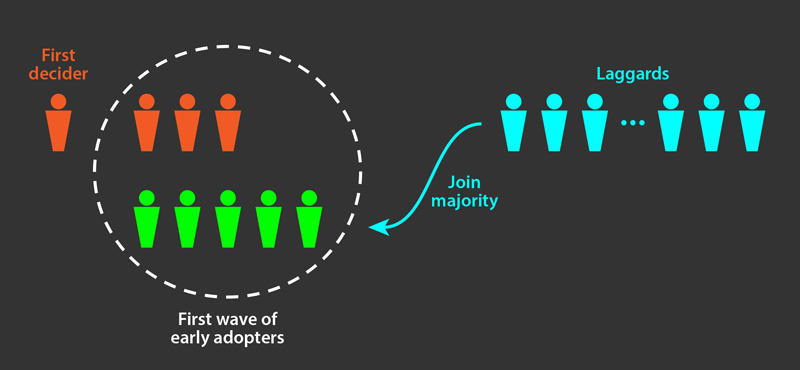
If the society is split into early adopters and laggards, however, the decision-making dynamics are different (Fig. 1). In the model, when an early adopter makes a decision, laggards modify their y by a value corresponding to the early adopter’s threshold, which is much smaller than their own threshold. In other words, laggards recognize that an early adopter’s decision is hasty and unreliable and assign a smaller weight to it. As a result, only the early adopters are strongly influenced by the first decisions, while laggards will only react when a sufficient number of early adopters have followed the first decider. Hence, smaller pools of adventurous explorers will form, exploring possible decisions and providing feedback that the laggards can follow. The model shows that, even with a poor initial decision, a larger fraction of the population, compared to the homogeneous case, will ultimately end up choosing the favorable option.
The results demonstrate how the skepticism of laggards can act for the greater good by basing the collective decisions on more reliable data. Nevertheless, early adopters remain essential: without their hasty decisions, there is no information for the laggards to exploit. Moreover, the speed of early adopters’ decisions allows the collective decision to be reached faster than if laggards are left to accumulate information by the slow process of individual research alone. Depending on the specifics of the population, the researchers find that there is an optimal adopter-laggard fraction that maximizes the decision-making outcome.
It would be interesting to devise experiments or observations to test whether heterogeneous groups make group-beneficial decisions in the real world, as predicted by the new model. An outstanding question is whether a key model assumption is justified: are people actually able to assign a lower weight to the first, risky decisions of the early adopters? Experience from public health campaigns [1] suggest this may be the case: it generally proves more effective to target laggards than early adopters, who, by virtue of their innovativeness, tend to be ignored by the rest of the society. At a time in which the widespread adoption of health measures and behavioral changes is critical, the insights coming from models like the one proposed by Karamched and colleagues could perhaps help public-health campaigners identify whom to target to spread their message most effectively.
References
- E. M. Rogers, Diffusion of innovations (Free Press, New York, 2003)[Amazon][WorldCat].
- H. Noorazar, “Recent advances in opinion propagation dynamics: A 2020 survey,” arXiv:2004.05286.
- B. Karamched et al., “Heterogeneity improves speed and accuracy in social networks,” Phys. Rev. Lett. 125, 218302 (2020).
- C. Castellano, “Statistical physics of social dynamics,” Rev. Mod. Phys. 81, 591 (2009).
- R. A. Blythe, “Colloquium: Hierarchy of scales in language dynamics,” Eur. Phys. J. B 88, 295 (2015).
- S. Redner, A guide to first passage processes (Cambridge University Press, Cambridge, 2001)[Amazon][WorldCat].
- R. P. Mann, “Collective decision making by rational individuals,” Proc. Natl. Acad. Sci. U.S.A. 115, E10387 (2018).
- S. J. Gershman et al., “Computational rationality: A converging paradigm for intelligence in brains, minds, and machines,” Science 349, 273 (2015).