50 Years of Physical Review B: Solid Hits in Condensed Matter Research

J. Tersoff and D. Hamann, Phys. Rev. B (1985)

J. Tersoff and D. Hamann, Phys. Rev. B (1985)

×

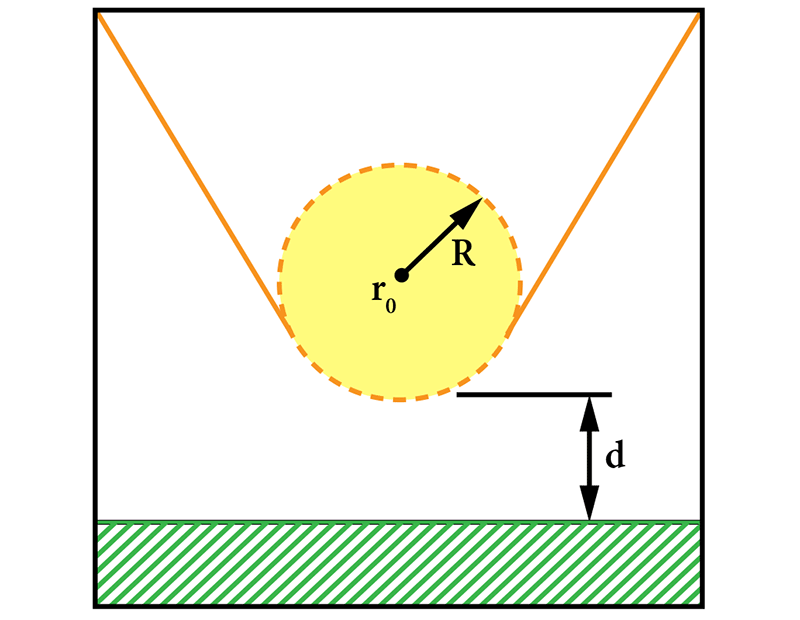
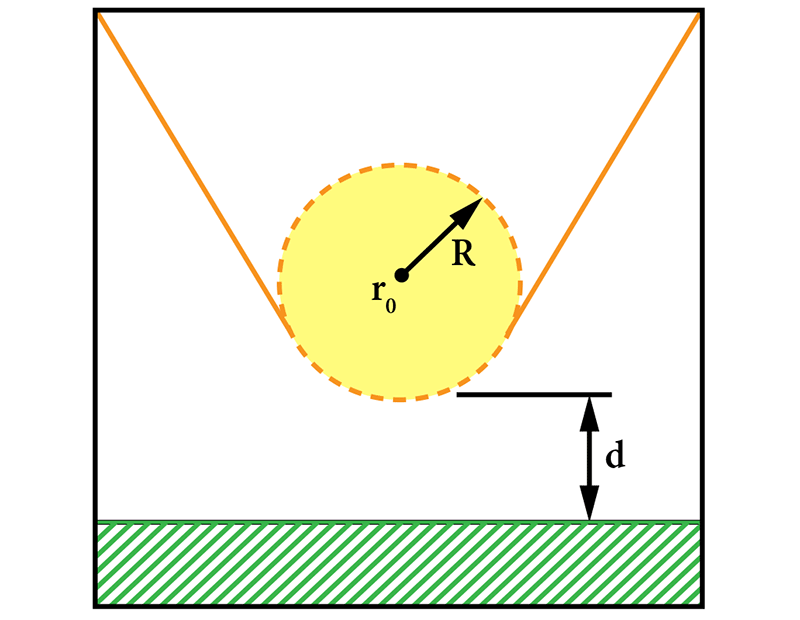
The early 1980s invention of the scanning tunneling microscope (STM) afforded an unprecedented view of a material’s surface. Seeing STM images with atomic resolution for the first time, “everyone was kind of blown away,” recalls Jerry Tersoff of IBM. In a 1985 paper, he and Donald Hamann, of Bell Labs, presented a theory to help interpret STM measurements. Surfaces had largely been studied via diffraction, and they were imagined to be neat arrangements of atoms. But thanks to the STM, the surface atomic structure could be seen directly. “Surfaces were nothing like what we had thought,” says Tersoff. “It was kind of scary to see how messy and complicated [they] were.”

An STM scans a needle with an extremely fine tip over a material. With careful preparation, the bottom-most atoms of the tip will, when brought close enough to the material’s surface, pick up an electron tunneling current that can be used to map the surface structure. While a postdoc at Bell Labs, Tersoff developed a simple theory to connect these measurements with information about a surface’s electronic states. “It was clear that the real interest in [STM] was experimental, and the purpose of the theory was just to let you go ahead and do your experiments and know what they meant,” says Tersoff. Making the theory simple enough to be useful necessitated certain simplifications. Tersoff and Hamann reasoned that, since the surface was the object of interest, they would simplify the tip and approximate it as a tiny sphere.

The Tersoff-Hamann model is a standard reference to get students up to speed on the theory of STM, says STM experimentalist Fabian Natterer of the University of Zurich. “I’ve used and seen [their figure] of a tip above a sample more often than I can remember.” Natterer, who got his Ph.D. in 2013, explores ways of adapting the STM to study magnetic surfaces and to build quantum matter one atom at a time. He enjoys the unpredictability of STM research, explaining that his group often changes course after stumbling on an interesting phenomenon. “We learn about all kinds of fields that [weren’t] on our radar,” he says. And like many childhood LEGO fans, he loves building things with tiny pieces—in this case single atoms.

J. Tersoff and D. Hamann, “Theory of the scanning tunneling microscope,” Phys. Rev. B 31, 805 (1985).

Since its development in the 1960s, density-functional theory (DFT) has become one of the most popular methods for predicting material properties—helping design and discover catalysts, superconductors, exotic compounds, and much more. “[DFT] is our workhorse and forms the vast majority of our calculations,” says Christopher Wolverton of Northwestern University, who studies materials related to batteries, solar fuels, and other energy technologies.

Like many materials-focused researchers, Wolverton and his group rely heavily on a computer program called the Vienna Ab initio Simulation Package (VASP). The licensed software grew out of a 1996 paper by Georg Kresse of the Vienna University of Technology and Jürgen Furthmüller of the Friedrich-Schiller University of Jena in Germany. In DFT, one finds an approximate solution to the many-body Schrödinger equation for an electronic system. As described in their paper, Kresse and Furthmüller figured out how to make this process much more efficient so that it could be done with larger and larger collections of atoms.

Wolverton says that VASP helped democratize DFT, bringing code into the hands of “essentially any researcher that wanted it.” This shift led to more creative applications of DFT and a flood of predictions. “The field of computational materials science really exploded,” he says. Today, VASP is used widely by materials scientists, physicists, and chemists, and Kresse and Furthmüller’s paper is one of the most highly cited articles in Physical Review B.

“I use [VASP] on an everyday basis,” says Mengen Wang, a postdoc at the University of California, Santa Barbara. Wang has previously used the code to better understand the steps in catalytic reactions. In her current research, it allows her to study the growth of a semiconductor that’s useful for high-power electronics. VASP’s popularity, she says, stems from its efficiency and its reliability—researchers know they can trust the accuracy of its calculations.

Wolverton adds that VASP facilitated the field of materials informatics, which aims to find desirable materials by combining swaths of materials data with analytical tools, such as machine learning. Several groups (including his own) have developed large databases of DFT calculations that “screen” for new and existing materials with certain properties. “Each of these databases is based on the VASP code,” says Wolverton.

G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. B 54, 11169 (1996).

R. Laughlin, Phys. Rev. B (1981)

R. Laughlin, Phys. Rev. B (1981)

×

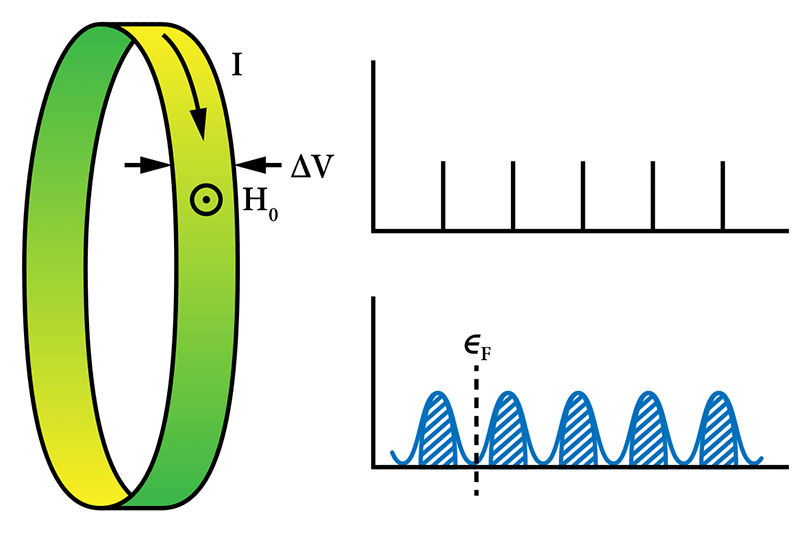
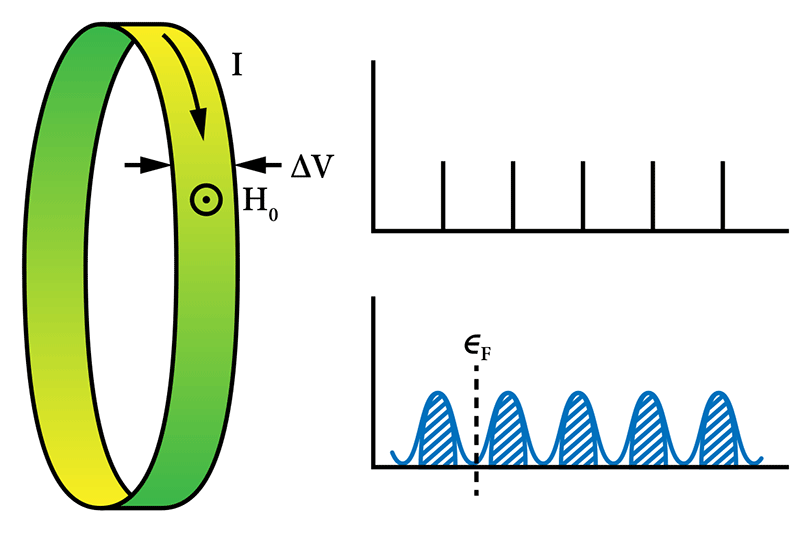
Take a strip of metal, run an electrical current through it, and then pierce the strip with a magnetic field. The moving charges will veer off to the sides, producing a so-called Hall voltage that should go up continuously as the field is made stronger or the current higher.

However, a repeat of this basic experiment when the temperature was very low, the strip very flat, and the field very strong revealed an astounding effect. Instead of changing continuously, the voltage only budged in quantized steps, plateauing at an extremely precise value in between. Those steps, reported in 1980, showed that the Hall conductivity (the ratio of the current to the Hall voltage) could only assume integer multiples of $e^2∕h$.

What’s striking about the Hall conductivity is that it’s insensitive to impurities. That feature suggested the quantum Hall effect (QHE) was due to a “fundamental principle,” wrote Robert Laughlin, then at Bell Labs, in an elegant 1981 paper—one of the first to explain the QHE. The principle turned out to be the gauge invariance of localized and extended electronic states. Laughlin’s insight provided the groundwork for his explanation of another exceptional result, the 1982 observation of the fractional quantum Hall effect. (For this theoretical work, Laughlin was awarded the 1998 Nobel prize.)

The quantum Hall system came to be known as the first example of a topological material, which has properties that remain constant despite some continuously changing parameter, like an external field. Physicists have since uncovered numerous other forms of such materials, such as topological insulators, which might be useful for hosting robust qubits for quantum computing. Since 2005, Physical Review B alone has published more than 5000 papers that mention topological insulators. The vast interest in the topic today was “unpredictable,” says Laughlin, now at Stanford University. Realizing the possibility of topological insulators, he adds, “took a confluence of unlikely events and actions made by other people.”

One scientist who jumped in was Taylor Hughes, of the University of Illinois, Urbana-Champaign. “When I first started working in this field in 2005, we were really concerned that topological insulators were just a theorist’s playground,” he says. “However, in the last 15 years, so many new topological materials have been predicted and discovered that it is almost easier these days to list things that aren’t topological!” (See more on this topic in this 2015 Q&A with Hughes, Topologically Speaking.)

R. B. Laughlin, “Quantized Hall conductivity in two dimensions,” Phys. Rev. B 23, 5632(R) (1981).

–Jessica Thomas is the Editor of Physics.