Quantum Computer Crosscheck
How can you check if two quantum devices produce equivalent results? This question comes up frequently in the race to build bigger and better quantum computers. For example, suppose you have a small quantum device that you know is working, but you want to improve it, say, by adding more quantum bits (qubits). Is the new device producing the same answers? Or suppose a manufacturer builds a device from a prototype. Will the two devices perform equally? Now a team of researchers led by Rainer Blatt and Peter Zoller at the Institute for Quantum Optics and Quantum Information of the Austrian Academy of Sciences in Innsbruck has found a novel solution to this dilemma [1]. Their method uses a simple set of randomly chosen measurements and is much more efficient than previous approaches. Their work makes it possible, for the first time, to directly compare quantum devices across platforms and even compare devices with different types of physical qubits sitting in different labs.
It might seem like cross-validating two quantum devices is straightforward: simply pick your favorite quantum computation and run it on both devices, then measure the output and check if the results are the same. Unfortunately, the intrinsic randomness of quantum mechanics means that both devices could be identical, but their outputs for a given run will be different. It’s only the probabilities for the various outputs that are the same. To address this randomness, you could use a statistical test to conclude that they give essentially identical distributions. This approach works—but only for that particular computation. But how can you be sure that both devices give equivalent results for all possible computations?
Prior work on this question initially focused on performing quantum state tomography or process tomography, which are the ultimate brute force tests for equality. These approaches involve measuring every possible parameter governing the qubit system in each device. For example, one can measure the correlation functions between each possible qubit. The problem is that this can require an enormous number of measurements. Even using advances such as compressed sensing [2], the effort for quantum state tomography requires at least 4n measurements to accurately estimate an arbitrary state of n qubits. Other approaches, such as matrix product state tomography [3], require relatively less measurements—scaling as a polynomial in n. But they only work when an unknown state is uniquely specified by few-body correlations (such as pair correlations between spins in a chain), in effect, truncating the allowed set of states on which the method works.
Researchers have come up with less computationally intense algorithms for testing the quality of a device by relaxing the goal of the problem to estimating a single statistical parameter called a fidelity. There is more than one definition of fidelity, but every fidelity is a measure that compares how much two quantum processes or quantum states overlap or agree with each other, with 1.0 being a perfect overlap. Methods for measuring fidelity, such as randomized benchmarking [4] and direct fidelity estimation [5], can be efficient (scaling polynomial in n), but they utilize “absolute” knowledge that compares the system to a known standard or to a prespecified ideal. Thus these methods are not immediately suited to comparing two unknown devices where only relative knowledge matters.
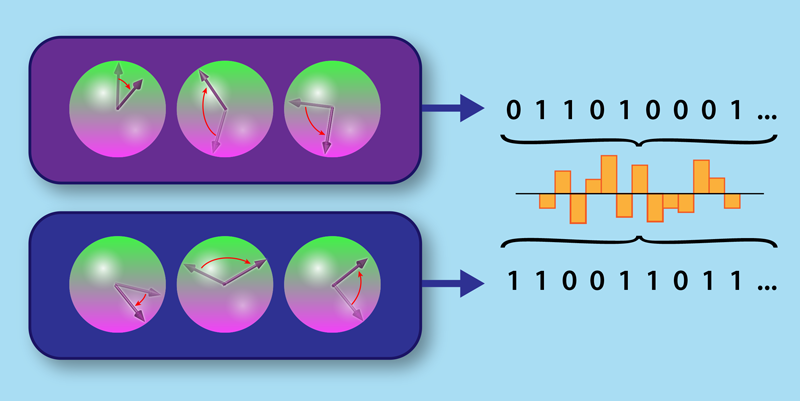
The Innsbruck team has developed a new program in which the fidelity measures the overlap between two completely unknown quantum systems. The method makes use of a simple measurement scheme. First, prepare a given state on each device and apply the same randomly chosen operation, such as a spin rotation, to the two systems (Fig. 1). Then measure both devices. The output statistics from these measurements enable the computation of the cross-correlations between the two systems, and these cross-correlations are sufficient to estimate a fidelity. The randomness of the operations ensures that every possible state is treated fairly by the protocol and that no “bad” state could bias the results.
The use of random operations—in particular "random local dynamics" that randomly affects only one spin at a time—is not new. For example, researchers have previously introduced random operations in the estimation of entanglement entropies, which are quantities that characterize how much of a system’s entropy is due to entangling correlations with external degrees of freedom [6]. The Innsbruck team developed this method further [7], but in this new work [1], they are the first to apply random local dynamics to two systems instead of just a single system. Furthermore, the authors provide numerical evidence that the number of required measurements for their cross-validation scheme scales like 2bn, where b is less than 1 for systems of interest. This compares favorably to other protocols like compressed sensing, where b=2.
As a demonstration of their protocol, the authors applied it to a trapped-ion quantum simulator experiment with ten qubits [8]. The ions in the system were aligned in a one-dimensional chain and placed in an antiferromagnetic configuration with alternating spin up and spin down. The spins evolved in time because of long-range spin-spin exchange interactions. To perform the necessary random operations on the qubits, the team applied a transverse magnetic field, which caused the spins to rotate by a controllable amount. After a certain amount of time, the spins in the system were all measured. As a first test, the team compared the experimental data to theoretical predictions. They found good agreement, as evidenced by a high initial fidelity of 0.97, where 1.0 indicates perfect agreement with an ideal theory state. Over time, the fidelity decreased as a result of complicated many-body entangled states, decoherence, and accumulated imperfections, but it still retained a relatively high value of 0.7. The team also compared the experiment to itself by looking at the results taken at two different times. Although not a true test of their cross-validation scheme, this experiment-experiment validation showed that the fidelity outcomes were reproducible.
The Innsbruck team has demonstrated a potentially new way to efficiently verify quantum devices, but their cross-validation scheme still faces many challenges. For example, the test has yet to be performed on two separate devices in different labs, and the data collection effort, while improved, is still demanding. And there may be competing options on the horizon. A recent breakthrough [9] has shown that few-body correlations within a single system can be estimated very efficiently with parallel measurements. Perhaps these parallel measurement schemes could be used to verify or cross-validate near-term devices? Looking beyond the near term, quantum computer scientists have recently shown that ideal quantum computers can, in principle, be verified efficiently by conventional computers [10]. Perhaps someday soon these protocols can be tested experimentally on real physical systems.
This research is published in Physical Review Letters.
References
- A. Elben et al., “Cross-platform verification of intermediate scale quantum devices,” Phys. Rev. Lett. 124, 010504 (2020).
- D. Gross et al., “Quantum state tomography via compressed sensing,” Phys. Rev. Lett. 105, 150401 (2010).
- M. Cramer et al., “Efficient quantum state tomography,” Nat. Commun. 1, 149 (2010).
- J. Emerson et al., “Scalable noise estimation with random unitary operators,” J. Opt. B 7, S347 (2005); “Symmetrized characterization of noisy quantum processes,” Science 317, 1893 (2007); E. Knill et al., “Randomized benchmarking of quantum gates,” Phys. Rev. A 77, 012307 (2008).
- S. T. Flammia and Y.-K. Liu, “Direct fidelity estimation from few Pauli measurements,” Phys. Rev. Lett. 106, 230501 (2011); M. P. da Silva et al., “Practical characterization of quantum devices without tomography,” 107, 210404 (2011).
- S. J. van Enk and C. W. J. Beenakker, “Measuring Tr 𝜌n on single copies of 𝜌 using random measurements,” Phys. Rev. Lett. 108, 110503 (2012).
- A. Elben et al., “Rényi entropies from random quenches in atomic Hubbard and spin models,” Phys. Rev. Lett. 120, 050406 (2018); “Statistical correlations between locally randomized measurements: A toolbox for probing entanglement in many-body quantum states,” Phys. Rev. A 99, 052323 (2019).
- T. Brydges et al., “Probing Rényi entanglement entropy via randomized measurements,” Science 364, 260 (2019).
- J. Cotler and F. Wilczek, “Quantum overlapping tomography,” arXiv:1908.02754.
- U. Mahadev, “Classical verification of quantum computations,” arXiv:1804.01082.