Using “Noise” to Detect Majorana States
Majorana bound states (MBSs) could be the qubits of the future. These unique electronic states are expected to be resistant to environmental perturbations that destroy the information in currently known qubits. However, MBSs have one major drawback: researchers are not sure to have actually observed them. Candidate states located at the ends of semiconductor-superconductor nanowires bear some characteristic features of MBSs, but they might be impostors instead. A new method—proposed by Jan Manousakis from the University of Cologne in Germany and colleagues—could potentially offer a way to distinguish real from fake MBSs by measuring statistical correlations between currents flowing in connected nanowires [1]. The advantage of this technique is that the states could be tested without the complication of trying to move them. Moving MBSs around each other in a particular way would be the ultimate test of authenticity, but such experiments have proven very difficult to do.
As originally envisioned, a Majorana fermion is a zero-energy, spin-1/2, charge-neutral particle [2]. Such a particle has never been observed, but there are collective electronic states that could embody the Majorana’s main characteristics. Specifically, the Majorana bound state is a quasiparticle, believed to be located at the boundary of a topological superconductor [3] or in a system described by similar theories [4] (see Majoranas in Majorca). MBSs are different from their eponym. They are spinless and do not have exactly zero energy in a realistic system. These differences are reflected in the evolution of terminology in the literature, from Majorana fermion to Majorana zero mode, to Majorana bound states nowadays.
MBSs do retain one “Majorana” characteristic: they obey non-Abelian statistics [5]. This means that two pairs of MBSs have a collective ground state that changes every time two MBSs from different pairs are rotated, or “braided,” around each other [6]. As such, the MBS pairs can act as a qubit that changes from, say, 0 to 1 when the braiding operation is performed. Since these qubit states would be immune to environmental perturbations, the use of MBSs for quantum computing has triggered a global effort along this direction.
Currently, the most promising experimental setup for observing MBSs—and the one that offered the first hints of their existence—consists of a semiconductor nanowire in the proximity of a superconductor [7]. The type of semiconductor is important: it must have a strong spin-orbit coupling and a large Zeeman effect (spectral line splitting in a magnetic field). The spin-orbit coupling locks the spin orientation of the charge carriers with respect to their momentum direction, which affects the way the electrons pair up in the superconductor. The end result is a switch from s-wave superconductivity—in which the superconducting energy gap is isotropic—to p-wave superconductivity—in which the gap depends on the momentum direction. Above a critical magnetic field, the p-wave superconductor in the nanowires can become topologically nontrivial, which means the “pattern” of the momentum dependence in the superconducting gap is characterized by a nonzero topological number [8]. Theory predicts that the boundaries of this topological superconductor—in this case the ends of the nanowire—should host MBSs.
The main argument behind MBS claims comes from tunneling measurements in which the nanowire is placed next to a conducting lead [9]. When the bias voltage between lead and nanowire is increased just above the zero-voltage point, researchers observe a sudden rise in the tunneling current, corresponding to a peak in the differential conductance. This “zero bias peak” is considered a signature of MBSs, as an MBS sitting at the end of the nanowire will act as a kind of intermediate step for the tunneling transition at zero energy.
Unfortunately, other mechanisms can also lead to zero bias peaks. For instance, the peaks could arise from Andreev bound states (ABSs), which occur at the interface between a normal superconductor and a normal metal. An ABS forms when one electron tunnels from the metal to form a Cooper pair of two electrons in the superconductor while a hole (or a vacancy of electron) is reflected to conserve the electric charge. Topologically, ABSs can be regarded as a superconducting version of the Jackiw-Rebbi soliton [10]. Although experimentalists have tried to rule out ABSs and other non-MBS explanations, not everyone is satisfied. The ambiguity has invoked many arguments and further theoretical proposals.
Manousakis and colleagues propose a new scenario to verify the MBSs [1]. The idea is to take advantage of the unique statistical properties of MBSs. The method, which would work for any zero-dimensional MBSs, involves measuring a physical quantity called the cross-correlation shot noise. Much like the annoying static in an old radio player from lightning or other disturbances, this noise is due to the influence of one current on another. Manousakis and colleagues show that an MBS signature can be extracted from this “noise” in a circuit of interconnected nanowires.
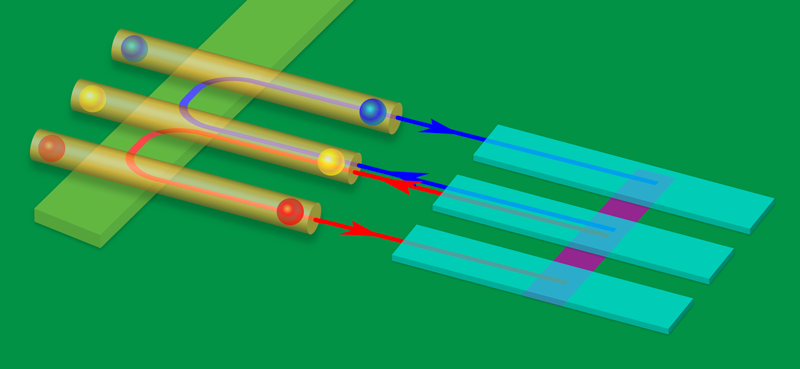
The team imagines three nanowires connected to each other through a superconducting backbone (Fig. 1). Each nanowire is placed next to a conducting lead so that a tunneling current can pass through the nanowire end, where the MBSs are located. The leads can be connected in various ways to control how the current passes through the entire system. The cross-correlation shot noise is a measure of how the current of an electrode connected to one MBS relates to the current in another electrode connected to a different MBS. The cross-correlation is known to be negative for noninteracting fermions and positive for noninteracting bosons due to differences in the quantum statistics of fermions and bosons. The situation is more complicated for MBSs because they are neither fermionic nor bosonic. The authors calculate a single parameter, called the Fano factor, which characterizes the cross-correlation noise. They find that the Fano factor exhibits different behaviors depending on whether the nanowires contain true MBSs or ABS impostors.
The proposed experiment can be compared to braiding experiments, which offer a possible alternative test of MBS existence. Braiding experiments, which would involve moving MBSs around each other in the crowded space of a nanowire network, require a more sophisticated setup and finer control of the electronic gates. Although efforts are ongoing, no successful braiding experiment has been reported. The protocol of Manousakis and colleagues avoids the difficulty of moving MBSs and, more importantly, is based on existing experimental systems with little modification.
Still, the new experiment would be challenging. Researchers have measured the cross-correlation noise for superconducting and fractional quantum Hall systems but never for Majorana setups. The measurement of currents in these nanometer devices is difficult, as the current comes from one-by-one tunneling of electrons. Trying to measure a correlation between the slow “drip” in two nanowires will be hard. And it is still not clear whether the methods used in nanowire experiments to eliminate unwanted noise might also kill the desired noise signal.
Of course, researchers will eventually have to braid MBSs if they ever want to use them for real applications in quantum computing. Once braiding is realized, all the doubts about the Majorana bound states will disappear.
This research is published in Physical Review Letters.
References
- J. Manousakis et al., “Weak measurement protocols for Majorana bound state identification,” Phys. Rev. Lett. 124, 096801 (2020).
- E. Majorana, “Teoria simmetrica dell’elettrone e del positrone,” Nuovo Cim. 14, 171 (1937).
- A. Y. Kitaev, “Unpaired Majorana fermions in quantum wires,” Phys. Usp. 44, 131 (2001); L. Fu and C. L. Kane, “Superconducting proximity effect and majorana fermions at the surface of a topological insulator,” Phys. Rev. Lett. 100, 096407 (2008).
- G. Moore and N. Read, “Nonabelions in the fractional quantum Hall effect,” Nucl. Phys. B 360, 362 (1991).
- A. Y. Kitaev, “Fault-tolerant quantum computation by anyons,” Ann. Phys. 303, 2 (2003); C. Nayak et al., “Non-Abelian anyons and topological quantum computation,” Rev. Mod. Phys. 80, 1083 (2008).
- D. A. Ivanov, “Non-Abelian statistics of half-quantum vortices in p-wave superconductors,” Phys. Rev. Lett. 86, 268 (2001).
- R. M. Lutchyn et al., “Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures,” Phys. Rev. Lett. 105, 077001 (2010); Y. Oreg et al., “Helical liquids and majorana bound states in quantum wires,” Phys. Rev. Lett. 105, 177002 (2010).
- J. Alicea, “Majorana fermions in a tunable semiconductor device,” Phys. Rev. B 81, 125318 (2010).
- V. Mourik et al., “Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices,” Science 336, 1003 (2012); M. T. Deng et al., “Anomalous zero-bias conductance peak in a Nb–InSb nanowire–Nb hybrid device,” Nano Lett. 12, 6414 (2012); A. Das et al., “Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions,” Nat. Phys. 8, 887 (2012).
- R. Jackiw and C. Rebbi, “Solitons with fermion number ½,” Phys. Rev. D 13, 3398 (1976).