Time Crystals in Open Systems
Time crystals, as proposed by Frank Wilczek in 2012, are temporal analogs of conventional space crystals [1]. Just as conventional crystals require the breaking of space translation symmetry, time crystals require the breaking of time translation symmetry (see Viewpoint: Crystals of Time). These exotic, dynamical phases of matter have been realized on various experimental platforms, but in all cases, the time crystal phases have been accommodated by closed systems that are subject to coherent manipulations (see Viewpoint: How to Create a Time Crystal) [2]. Hans Keßler from the University of Hamburg, Germany, and his colleagues have now reported the first observation of time-crystalline behaviors in an open quantum system [3].
Time crystals can break continuous symmetry when realized in a time-independent (energy-conserving) system and break discrete time translation when realized in a periodically driven (Floquet) system. The former, as conceived by Wilczek, was proven to be impossible to achieve in ground states or thermal-equilibrium states of short-range interacting systems [4]. But the latter, in which the constituents adopt a recurring spatial configuration with a period that is a multiple (typically double) of the driving period, has been demonstrated in some closed spin systems with strong disorder and interactions [5]. To distinguish these “discrete time crystals” from other dynamical phenomena such as Rabi oscillations, this period multiplication must exhibit “rigidity”; that is, it must be robust against small perturbations in system parameters or driving protocols. A widely used recipe to create discrete time crystals with the necessary rigidity is to drive a symmetry-broken system to switch from one symmetry-broken state to another per driving period.
All experimental demonstrations of discrete time crystals so far have used closed systems, leaving open the question of whether they can be achieved in the presence of dissipation and decoherence. This fundamental question has practical importance, since real systems can never be completely isolated from their surroundings. While dissipation generally destroys a time crystal’s order, there are situations where the order is retained if the system-environment coupling can be tailored appropriately. In quantum computing and quantum-state engineering, such tailoring already allows dissipation to be harnessed as a useful resource [6]. Recent developments in experimental atomic, molecular, and optical physics have now made it possible to use this approach to realize novel dynamical order in open quantum systems [7].
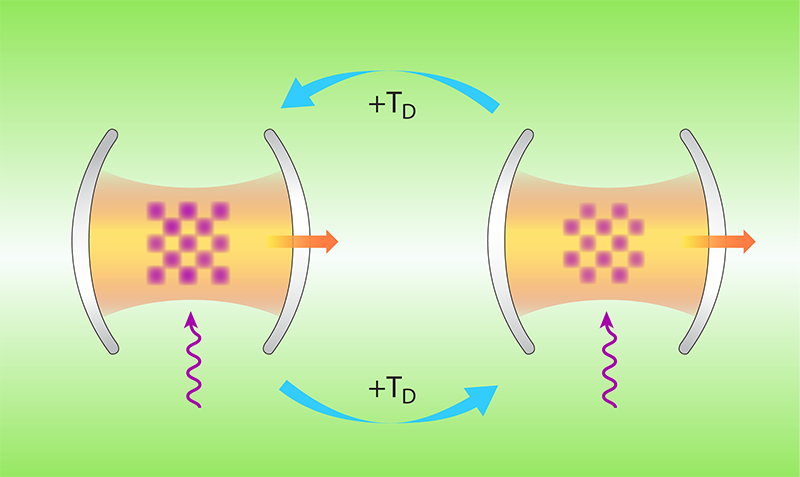
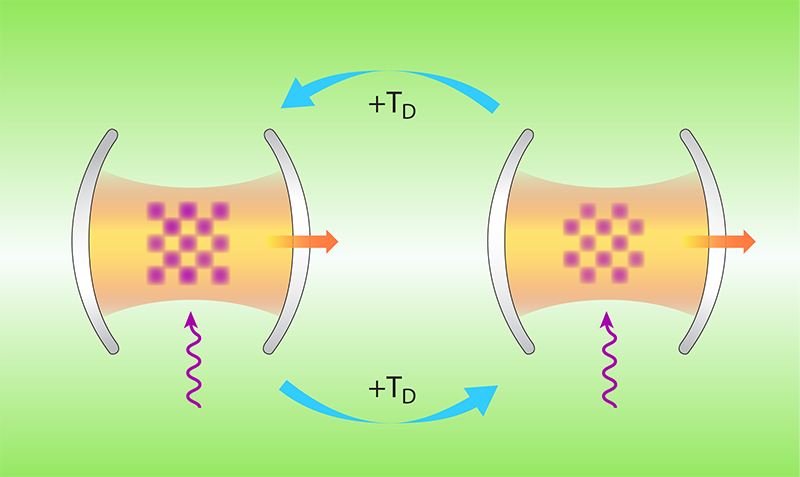
Taking advantage of these developments, Keßler and colleagues provide strong evidence that a discrete time crystal can exist in a driven, open, atom-cavity system. Their experiment follows theoretical predictions of time-crystalline order in a driven open Dicke model [8]. In its basic (non-time-crystalline) form, the open Dicke model describes an ensemble of two-level atoms driven by a pump laser and coupled to a single lossy photon mode. This system exhibits a dissipative, superradiant phase transition, meaning that beyond a certain pump threshold, the atomic ensemble becomes spatially ordered and the atoms emit photons coherently. As in the first experimental demonstration of this phase transition [9], Keßler and colleagues use a Bose-Einstein condensate (BEC) in a cavity, with the two levels manifested in the atoms’ motional degrees of freedom. But, whereas that first demonstration was static, Keßler and colleagues drive their system by temporally varying the strength of the pump laser that induces the coupling between atoms and cavity photons.
The team measured the dynamics of the system using two methods. First, they continuously monitored the phase and number of intracavity photons by detecting photons leaking out of the cavity. Second, they measured the momentum distribution of the atoms at a given instant of time by releasing the BEC and observing its expansion (i.e., the time-of-flight image).
These measurements reveal that, for properly chosen parameters, the system periodically switches between two symmetry-broken superradiant states, with the BEC taking on a different checkerboard pattern in each state. The complete cycle of switching between states is twice the driving period and is robust against aperiodic temporal disorder in that driving period. While this robustness is different from the usual rigidity seen in discrete time crystals, where the perturbed system is strictly periodic [5], it is analogous to the robustness of space crystals, which can tolerate spatially inhomogeneous impurities.
The period-doubling behavior observed by the team is reminiscent of a phenomenon seen in nonlinear optics, in which a subharmonic generator produces output photons whose frequency is an integer fraction (typically one half) of that of the input photons. However, there is a conceptual difference: Discrete, time-crystalline oscillations are a dynamical property of the system itself, whereas subharmonic generation is directly related to the output signal rather than to the system (where the “system” is the medium that converts the input photons). Moreover, the decisive condition for time crystals—that they be robust against disturbances—is not required for subharmonic generation. Nevertheless, it might be interesting to consider whether insights gained by creating discrete time crystals could help achieve efficient subharmonic generation.
A limitation of the time crystal demonstrated by Keßler and his colleagues is that the oscillations decay after a few periods. This decay occurs mainly from atom loss from the BEC, which effectively reduces the collective atom-photon coupling in the system and pushes it out of the superradiant phase. To prolong the lifetime of this time crystal, an important future task is to overcome this atom loss. It would also be interesting to tune both the photon loss from the cavity and the interatomic interactions (whose impact is overshadowed by the atom loss in the present experiment). Such tuning might uncover novel phenomena not predicted by the standard semiclassical (mean-field) description [10] and confirm that the time-crystalline order is indeed stabilized by dissipation [8]. Beyond the periodically driven system employed by Keßler and his colleagues, researchers are yet to demonstrate a continuous time crystal in a time-independent open system [11]. Although such time crystals have been shown to be impossible to achieve in equilibrium systems [4], they should be achievable in a system that is away from thermal equilibrium.
From a broader perspective, the experiment provides a prototypical example for investigating a rich interplay between driving, interaction, and dissipation in a quantum many-body system under continuous monitoring. We expect that this work will stimulate further theoretical and experimental studies on the largely unexplored phase structures and dynamical phenomena in nonequilibrium open quantum systems.
References
- F. Wilczek, “Quantum time crystals,” Phys. Rev. Lett. 109, 160401 (2012).
- J. Zhang et al., “Observation of a discrete time crystal,” Nature 543, 217 (2017); S. Choi et al., “Observation of discrete time-crystalline order in a disordered dipolar many-body system,” 543, 221 (2017).
- Hans Keßler et al., “Observation of a dissipative time crystal,” Phys. Rev. Lett. 127, 043602 (2021).
- H. Watanabe and M. Oshikawa, “Absence of quantum time crystals,” Phys. Rev. Lett. 114, 251603 (2015).
- N. Y. Yao et al., “Discrete time crystals: rigidity, criticality, and realizations,” Phys. Rev. Lett. 118, 030401 (2017).
- F. Verstraete et al., “Quantum computation and quantum-state engineering driven by dissipation,” Nat. Phys. 5, 633 (2009).
- H. P. Lüschen et al., “Signatures of many-body localization in a controlled open quantum system,” Phys. Rev. X 7, 011034 (2017).
- Z. Gong et al., “Discrete time-crystalline order in cavity and circuit QED Systems,” Phys. Rev. Lett. 120, 040404 (2018).
- K. Baumann et al., “Dicke quantum phase transition with a superfluid gas in an optical cavity,” Nature 464, 1301 (2010).
- B. Zhu et al., “Dicke time crystals in driven-dissipative quantum many-body systems,” New J. Phys. 21, 073028 (2019).
- F. Iemini et al., “Boundary time crystals,” Phys. Rev. Lett. 121, 035301 (2018).