Thermodynamic Limits to Anomalous Diffusion
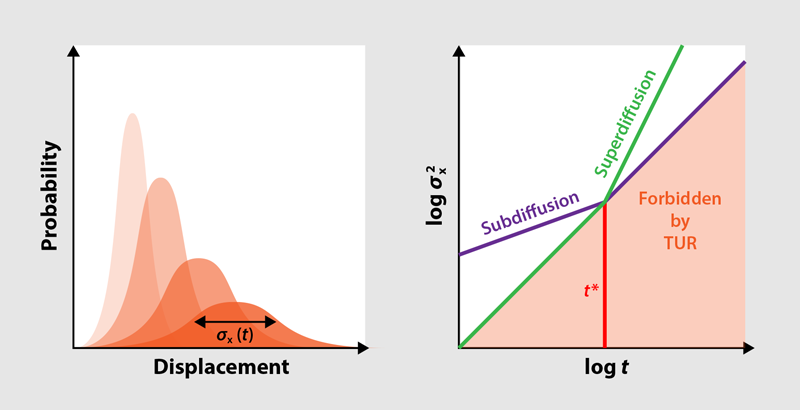
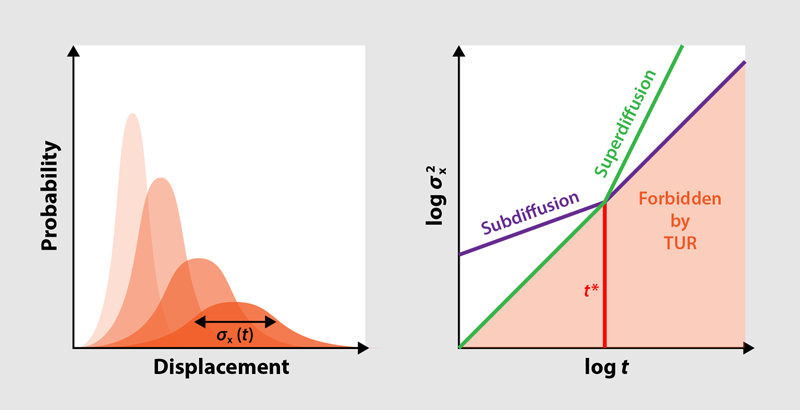
Diffusion is a commonplace phenomenon: Put a droplet of ink into a tank of water, and it will simultaneously spread out and become more and more diluted (Fig. 1). This means that the probability of finding a given ink particle at some position evolves from a sharply peaked distribution to a very broad one (Fig. 2, left). Typically, the width of this distribution, quantified by the variance, increases linearly with time, in line with an empirical law known as Fick’s second law of diffusion. But this law can be defied by systems ranging from the microscopic (such as biological cells) to the macroscopic (such as astrophysical plasmas), which exhibit anomalous diffusion processes where the variance increases nonlinearly with time [1]. New research by David Hartich and Aljaž Godec, at the Max Planck Institute for Biophysical Chemistry in Germany, shows that the period over which anomalous diffusion can occur is bounded and that these bounds have deep connections to the underlying thermodynamics of the diffusive system [2].
Hartich and Godec arrive at this result by studying anomalous diffusion through the lens of the thermodynamic uncertainty relation (TUR) [3]. This relation applies to stochastic systems driven by some force (such as a mechanical force, a chemical reaction, or a voltage) into a stationary nonequilibrium state. Such systems produce observable outputs that accumulate over time, called “currents.” Examples of currents include the distance traveled by a random walker or the number of molecules produced in an enzymatic reaction. At a finite temperature, these currents are always fluctuating, and their relative uncertainty can be quantified in terms of the variance divided by the squared mean value of the current. The TUR states that this uncertainty multiplied by the energy used for driving the system (measured in units of the thermal energy ) is always . Thus, the TUR expresses a universal trade-off between precision and energetic cost: The current can only be quantified with high precision in more energetically driven systems.
The first paper conjecturing the TUR [4] (and the subsequent paper that provided its mathematical proof [5]) focused on applications to biomolecular processes. But the relation’s wider implications for statistical physics—for heat engines or general Langevin systems, for instance—soon became clear. Researchers have since developed variations of the TUR that push the limits of its applicability to quantum systems and nonstationary states. Yet the implications of the TUR for anomalous diffusion have so far remained unexplored.
The settings for which the TUR has so far been studied involve currents whose mean and variance, to a rough approximation, both increase linearly with time. Because such systems exhibit an ever-decreasing relative uncertainty (defined as the variance divided by the squared mean), the TUR can only be satisfied by an ever-increasing energetic cost, yielding an uncertainty-energy product that varies little over time. One may wonder how anomalous diffusion, in which the variance increases nonlinearly by definition, could ever fit into this picture. The simple but striking answer given by Hartich and Godec: It doesn’t—at least not for arbitrary timescales. For the TUR to hold, anomalous diffusion can only occur within a limited time window.
The researchers analyze the two general types of anomalous diffusion—subdiffusion and superdiffusion—for which the TUR yields two complementary bounds (Fig. 2, right). In subdiffusion, which can be seen in, for example, the diffusion of macromolecules in crowded intracellular environments, the variance increases more slowly than it does in normal diffusion. To understand the consequences of this slower increase with respect to the TUR, consider a 1D system of particles undergoing diffusion driven by an external force. If the particles cannot pass one another on the line, research has shown that the variance of their displacement increases with the square root of the time, which is slower than the normal linear increase. Because the mean displacement still increases linearly, the relative uncertainty in this system decreases more quickly than usual. At the same time, the energetic cost of driving the diffusion also increases only linearly. Inevitably, the TUR would be violated beyond a certain critical time ( ), which can be estimated with a simple formula. Hartich and Godec conclude that in order to avoid this violation, subdiffusion must come to an end at this point in time at the latest. In the context of this 1D system, the point at which subdiffusion ends corresponds to the point at which the blocking of one particle by another no longer inhibits further diffusion.
The researchers show that for superdiffusive transport, the opposite is true. This kind of anomalous diffusion is exhibited by, for example, biomolecules subject to active transport within cells, but it can be abstracted as a particle system in which the 1D environment of the subdiffusive case is replaced by a comb-like geometry: Particles diffuse along a central trunk or backbone, but they may also spread along dead-end side branches. Here, the uncertainty increases more quickly than usual. This rapid increase poses no problem over long timescales because the product of the relative uncertainty and the driving energy keeps increasing beyond 2. However, early on, it means that the uncertainty would have been smaller than allowed by the TUR. Hence, the critical time sets a lower bound on the onset of superdiffusion.
With these new bounds on subdiffusion and superdiffusion times (Fig. 2, right), Hartich and Godec bring the established field of anomalous diffusion into the same thermodynamic framework that encompasses regular diffusion. Just like the TUR itself, their result holds for any kind of driving, however far from thermal equilibrium. The result is also simple, in the sense that one only needs to know the energetic cost of the driving force in order to formulate the constraints on the diffusion process. Although these constraints will necessarily be loose in many situations, further research will show whether additional information about a system can be used to refine them. For instance, it would be interesting to see whether thermodynamics provides bounds not only on the time window but also on the mathematical properties of the anomalous diffusion observed within this time window. If this is the case, the newfound link between thermodynamics and anomalous diffusion could lead to a solid, joint theoretical foundation. Such a theoretical basis could be relevant for applications in cellular biophysics, where a common phenomenon is the transport of molecules in crowded environments subject to a limited availability of chemical fuel.
References
- R. Metzler and J. Klafter, “The random walk’s guide to anomalous diffusion: A fractional dynamics approach,” Phys. Rep. 339, 1 (2000).
- D. Hartich and A. Godec, “Thermodynamic uncertainty relation bounds the extent of anomalous diffusion,” Phys. Rev. Lett. 127, 080601 (2021).
- J. M. Horowitz and T. R. Gingrich, “Thermodynamic uncertainty relations constrain non-equilibrium fluctuations,” Nat. Phys. 16, 15 (2019).
- A. C. Barato and U. Seifert, “Thermodynamic uncertainty relation for biomolecular processes,” Phys. Rev. Lett. 114, 158101 (2015).
- T. R. Gingrich et al., “Dissipation bounds all steady-state current fluctuations,” Phys. Rev. Lett. 116, 120601 (2016).