Excavating Topology to Find Structure
Upon casual glance, the stars in the night sky might appear randomly placed. But look more carefully, and patterns—known as constellations—emerge in the sky. The building blocks of many soft materials, including glasses, granular media, and biological tissues, also appear randomly arranged yet often contain similar hidden patterns. Now Dominic Skinner at the Massachusetts Institute of Technology and colleagues introduce a technique that can reveal some of that subtle order [1]. Their computationally tractable method combines centuries-old mathematical ideas about soil transport and supply-chain optimization with more modern notions of topology in random networks (Fig. 1). Their work adds to a growing list of geometric and topological tools used to characterize soft materials.
Patterns and structures are key to understanding the mechanical and dynamical properties of many systems. For example, when logs flow in a river, their orientation with respect to one another determines whether they jam the river or whether they flow smoothly downstream; for metals, the topology of defects in the arrangement of their atoms determines, among other things, whether the metals stretch or fracture when a load is applied. Researchers have explained how the geometry and topology of structural motifs in ordered soft materials, such as a coherently swimming bacterial swarm or an oriented liquid crystal, relate to a material’s emergent macroscopic properties [2, 3]. However, extending this understanding to disordered soft systems is a notoriously challenging problem.
But there have been some breakthroughs. Data-driven approaches, including machine learning, have been successful in characterizing structural motifs in systems ranging from glasses [4] to leaf venation [5]. And recently, high-resolution imaging techniques have also allowed researchers to uncover and quantify the link between the shape and connectivity of cells in an epithelial monolayer to understand the factors determining the rigidity or fluidity of the layer. [6, 7]. The new technique from Skinner and colleagues fits in with this research effort. It provides a way to quantify the arrangement of cells in a tissue or of particles in disordered media and to use that quantification to classify properties such as the material’s phase behavior.
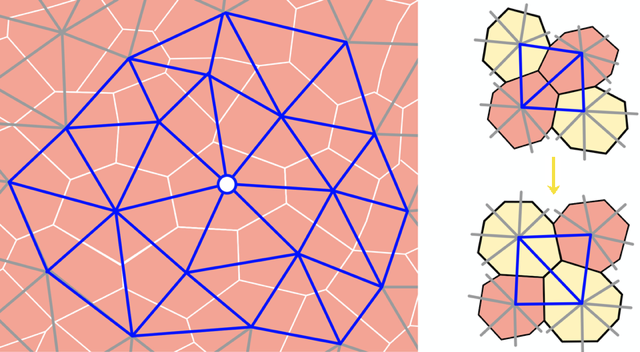
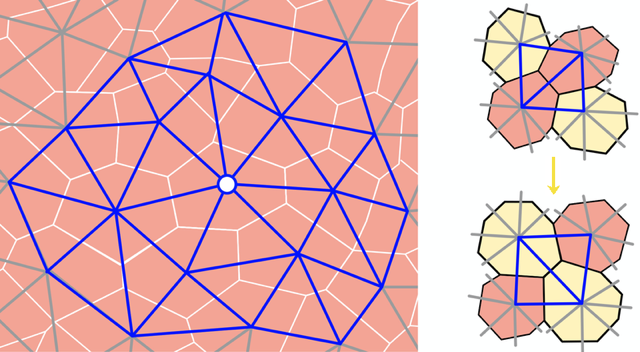
In their study, the team approximated a 2D epithelial layer with a 2D network of triangles. They also studied jammed granular packings and collections of self-propelled particles, such as bacteria, to demonstrate the versatility of their technique. The nodes of the network represent the central points of the cells or particles and the edges connect them to their neighbors (Fig. 2). The team calculated the spatial variations in the number and geometry of a cell’s contacts over the entire tissue to obtain a statistical representation of the network’s local structure.
That representation allowed the team to quantify a given network, but they also wanted to compare two different networks, for example those from two different tissues or those from the same tissue at two different times. To do that, they studied the local arrangement of vertices in the network by counting the number of “edge flips” needed to transform one network into another. An edge flip occurs when the dividing line between two triangles in a polygon switches the corners of the polygon that it connects (Fig. 2). These events take place naturally in cellular systems when two cells exchange neighbors.
Enumerating and comparing the catalog of possible contact networks for two different systems (for example, two different epithelial monolayers) is a computationally prohibitive task in all but the most trivial of situations. To get around this issue, Skinner and his colleagues turned to the problem of optimal mass transport.
The problem of optimal mass transport has a long and rich history: It was posed in the 18th century by the mathematician Gaspard Monge, who wanted to optimize the transport of soil for construction; but it was in the 1930s when the mathematician and economist Leonid Kantorovich found the answer. The problem, now known as the Monge–Kantorovich problem, has deep connections to resource allocation, optimization theory, and hydrodynamics, along with a range of applications in image analysis and machine learning [8]. By framing their network-topology-comparison problem as an optimal transport one, Skinner and colleagues were able to leverage existing tools to find a computationally efficient solution that is both practical and interpretable.
With their method, the team show that by analyzing a series of static images of networks (temporal snapshots of a tissue during its development, for example), they can detect an arrow of time. They can also identify phase boundaries and phase-separated states, and they can distinguish jammed mixtures made from particles of different shapes and sizes, such as M&Ms and rice grains. While such particle-identity discrimination is possible with other methods, the approach of Skinner and his colleagues can quantitively distinguish the networks that characterize these two systems “blindly,” without ever knowing that one network is for M&Ms and the other is for rice. This achievement is significant as both networks quantify subtle structural features in these disordered systems, and they connect them back to large-scale properties of the materials. The method is also attractive because of its computational tractability.
It is clear that the new method is a promising data-driven tool for classifying structural properties of soft systems. But more work is needed to understand the method’s limits, as well as its broader relevance. The ability to discern the chronological sequence of events from static snapshots offers a way to quantify irreversibility in dissipative systems, which is an attractive avenue for further exploration. A deeper understanding of the connection the team makes between optimal mass transport and statistical geometry is also a worthwhile goal.
It would also be interesting to combine this method with other information-theoretic-based techniques that have recently been proposed to capture hidden order [9]. While the use of topological edge flips was motivated by naturally occurring cell behaviors, related phenomena are prevalent in many fields, such as in discretized quantum gravity (where they capture the fluctuating geometry of spacetime) and in crystallography (where they give rise to defects with atomic rearrangements similar to those in Fig. 2). It may thus be fruitful to relate edge flips in tissues to defects present in crystals and other soft matter [3]. Finally, recent work has highlighted the relevance of optimal transport in deciphering the genetic lineage of cells during embryonic development [10], suggesting that biology may have more uses for earth-moving mathematics hidden up her sleeve.
References
- D. J. Skinner et al., “Topological metric detects hidden order in disordered media,” Phys. Rev. Lett. 126, 048101 (2021).
- K. Bertoldi et al., “Flexible mechanical metamaterials,” Nat. Rev. Mater. 2, 17066 (2017); S. R. Nagel, “Experimental soft-matter science,” Rev. Mod. Phys. 89, 025002 (2017).
- S. Shankar et al., “Topological active matter,” arXiv:2010.00364.
- S. S. Schoenholz et al., “A structural approach to relaxation in glassy liquids,” Nat. Phys. 12, 469 (2016); E. D. Cubuk et al., “Structure-property relationships from universal signatures of plasticity in disordered solids,” Science 358, 1033 (2017).
- E. Katifori and M. O. Magnasco, “Quantifying loopy network architectures,” PLOS ONE 7, e37994 (2012); J. W. Rocks et al., “Revealing structure-function relationships in functional flow networks via persistent homology,” Phys. Rev. Research 2, 033234 (2020).
- M. C. Gibson et al., “The emergence of geometric order in proliferating metazoan epithelia,” Nature 442, 1038 (2006); L. Atia et al., “Geometric constraints during epithelial jamming,” Nat. Phys. 14, 613 (2018).
- D. Bi et al., “A density-independent rigidity transition in biological tissues,” Nat. Phys. 11, 1074 (2015); J. A. Park et al., “Unjamming and cell shape in the asthmatic airway epithelium,” Nat. Mater. 14, 1040 (2015); L. Yan and D. Bi, “Multicellular rosettes drive fluid-solid transition in epithelial tissues,” Phys. Rev. X 9, 011029 (2019).
- C. Villani, Optimal transport: Old and new, Vol. 338 (Springer Science & Business Media, Berlin, 2008)[Amazon][WorldCat].
- S. Martiniani et al., “Quantifying hidden order out of equilibrium,” Phys. Rev. X 9, 011031 (2019).
- G. Schiebinger et al., “Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming,” Cell 176, 928 (2019).