A Unifying View of Thin-Plate Fracture
Tearing a piece of paper is a common experience of mechanical fracture. But describing the fracturing process poses a challenge for mechanical theories. The difficulty lies in the fact that its modeling involves two frameworks that aren’t easily brought together. The first is a geometrical framework that represents the whole sheet as a mathematical surface that, under stress, bends out of its plane—for example, by buckling, wrinkling, or crumpling. In contrast, the second framework, called linear elastic fracture mechanics, models smaller spatial scales within the sheet, describing how diverging stresses trigger a propagating crack. Now, Yael Klein and Eran Sharon of the Hebrew University of Jerusalem propose a way to unify the out-of-plane and in-plane frameworks [1]. The duo shows that the fracture can be incorporated into a geometrical description by “translating” the fracture-induced material deformation into equivalent changes of the material’s curvature. The elegant description based on a purely geometric quantity allows the researchers to successfully model a series of experiments on millimeter-thick polymer strips, explaining why—depending on the conditions—the strips may either buckle or fracture into pieces. This geometrical approach may be extended to tackle so-far intractable cracking problems in slender structures such as plates and shells.
A classical mechanics approach describes the deformation of a material in terms of a change of distances. In such an approach, the deformation is quantified by considering the movement of neighboring points in the material: The stress-induced change in the points’ mutual distances defines the strain. More recently, however, researchers have developed an alternative approach [2] that quantifies deformation not in terms of a change of distances but in terms of a change of metric—the way of computing the distance between two points.
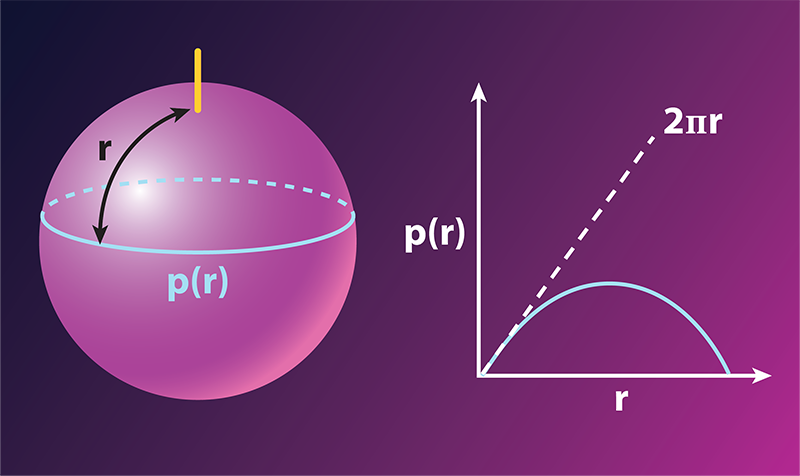
Measuring deformation in terms of a change of distances or of metrics is fully equivalent. But the notion of metrics comes with the beautiful and useful tools of differential geometry, including Gauss’s Theorema Egregium, or “remarkable theorem.” Gauss’s theorem states that measuring the distance on a surface gives information about the 3D deployment of the surface in space, that is, the surface’s curvature. To understand the meaning of the theorem, imagine measuring the length p of a latitude line that encircles Earth at points lying at a distance r from the North pole (Fig. 1, left). That distance isn’t equivalent to 2𝜋r, as it would be for a planar surface. Rather, p reaches a maximum value at the equator and then decreases beyond that (Fig. 1, right). By simply measuring distances along the surface, one can deduce that Earth isn’t flat. (The exact dependence of p on r can also reveal the object’s curvature: Earth’s smaller-than- 2𝜋r perimeter indicates a spherical object, while a larger-than- 2𝜋r perimeter would point at a saddle shape).
A powerful implication of Gauss’s theorem is that curvature stays the same if one bends a surface without stretching it. That’s why there cannot be a flat map of Earth without distance distortion. This curvature invariance previously allowed researchers to rephrase deformation in terms of geometry—an approach that has proven very useful to describe the mechanics of thin plates. For instance, the formation of wrinkles [3, 4] and of crumpling singularities [5, 6] can be explained using Gauss’s theorem: It is impossible to fold a flat sheet (zero Gaussian curvature) onto a sphere or a saddle without deforming the plate. Conversely, in biology, the morphogenesis of organs into 3D curved shapes is due to the fact that the nonuniform growth of living tissue leads to a change of metric [7]. Current research on morphable plates actively makes use of these ideas, describing material distortion in terms of a change from a flat, or Euclidian, metric of an initial shape toward a nonflat, or non-Euclidean, metric of the final shape [8].
Klein and Sharon now demonstrate that fracture can be incorporated in this geometrical framework. When fracture propagates in a material, the stress is amplified around the crack front. Conventional theoretical approaches model crack propagation by computing the stress field within the sheet around the crack tip. These approaches describe the material’s in-plane deformation using the linear theory of elasticity, except for the vicinity of the crack front, where all dissipation occurs. Such an approach successfully describes brittle fracture (in which the crack length is large compared to the plastically deformed region around the crack tip). But extending this approach to the fracture of thin plates is difficult because these plates tend to bend out of plane. This bending can only be described on the global scale of the sheet, which linear elastic models can’t do [9]. The researchers overcome this difficulty by showing that crack-induced deformations have an equivalent description in terms of a distribution of Gaussian curvatures along the path of the cracks.
Mathematicians and tailors alike know that cutting off a portion of a planar sheet and sewing the seam back together creates Gaussian curvature because the distances between points on each side of the seam have been irreversibly shortened. When stitched back together, the sheets form curved bodies without wrinkles. The subtle idea of Klein and Sharon is that—similarly to the addition or subtraction of material—the reversible elastic deformation that accompanies fracture can be translated into changes of Gaussian curvature by defining a new metric that accounts for the varying distances between the various material elements. The resulting formalism can thus account for both bending and fracture simultaneously.
To test the new geometry-based formalism, the researchers slowly immersed sheets of soft gel, with thicknesses of between 0.1 and 2 mm, in a solution of polyethylene glycol. The immersion into this concentrated solution caused the water contained in the gel to be expelled, so the gel sheet shrank. The researchers modeled the shrinking by defining a new reference metric plate. In this dynamic dipping process, the gel sheet’s shrinking was not uniform, and the highly distorted metric resulted in a strong Gaussian curvature.
The experiments revealed that thin samples eventually bend into curved bottle shapes (Fig. 2). Thicker plates, however, tend to stay flat because of the large energy cost needed for bending. Rather than bending, they form cracks. Thanks to the new geometric approach, the researchers could derive a phase diagram for these thin plates, which can reliably predict—from thickness and other material parameters—whether the dominant response to shrinking is buckling, stretching, or fracturing. In Klein and Sharon’s framework, this behavior has a simple explanation: The Gaussian curvature due to shrinking is to a large extent canceled by a Gaussian curvature with opposite sign that arises from fracture.
The new Gaussian language developed by Klein and Sharon may allow researchers to treat fracture and buckling within a universal framework. Such a framework could tackle complex fracture problems in thin structures, such as curved shells, that are relevant to both industry and biology. In particular, it could explain the formation of cracks during the manufacture of metallic shells or the rupture of seedpods that leads to the dispersal of seeds.
References
- Y. Klein and E. Sharon, “The buckling-fracture transition and the geometrical charge of a crack,” Phys. Rev. Lett. 127, 105501 (2021).
- E. Efrati et al., “Elastic theory of unconstrained non-Euclidean plates,” J. Mech. Phys. Solids 57, 762 (2009).
- H. King et al., “Elastic sheet on a liquid drop reveals wrinkling and crumpling as distinct symmetry-breaking instabilities,” Proc. Natl. Acad. Sci. U.S.A 109, 9716 (2012).
- J. Hure et al., “Stamping and wrinkling of elastic plates,” Phys. Rev. Lett. 109, 054302 (2012).
- T. A. Witten, “Stress focusing in elastic sheets,” Rev. Mod. Phys. 79, 643 (2007).
- M. Ben Amar and Y. Pomeau, “Crumpled paper,” Proc. R. Soc. Lond. A 453, 729 (1997).
- U. Nath et al., “Genetic control of surface curvature,” Science 299, 1404 (2003); J. Dervaux and M. Ben Amar, “Morphogenesis of growing soft tissues,” Phys. Rev. Lett. 101, 068101 (2008); C. Collinet and T. Lecuit, “Programmed and self-organized flow of information during morphogenesis,” Nat. Rev. Mol. Cell Biol. 22, 245 (2021).
- Y. Klein et al., “Shaping of elastic sheets by prescription of non-Euclidean metrics,” Science 315, 1116 (2007); J. Kim et al., “Designing responsive buckled surfaces by halftone gel lithography,” 335, 1201 (2012).
- B. Roman, “Fracture path in brittle thin sheets: A unifying review on tearing,” Int. J. Fract. 182, 209 (2013).