Driving Transport with High Disorder

Horacio M. Pastawski

Viewpoint

Driving Transport with High Disorder

Enrique Gaviola Institute of Physics, CONICET and National University of Córdoba, Córdoba, Argentina

April 12, 2021• Physics 14, 57

A study of long-range interactions in disordered systems yields a surprising result: Transport can increase with disorder.

Figure caption — **Figure 1:** A disordered system with long-range hopping is depicted as a set of $N = 7$ orbitals (green) in a star configuration (left). The disorder ( $W$ ) is depicted in the random size of the orbitals, while nearest neighbor hopping ( $Ω$ ) and long-range, all-to-all hopping ( $𝛾 ∕ 2$ ) are shown, respectively, with red and blue connections. The resulting excited band is separated from the ground state by an energy gap $Δ = N 𝛾 ∕ 2$ (middle). The current through the system is plotted against the disorder on a log-log scale (right). Different regimes are evident: Anderson localization, disorder-enhanced transport (DET), and disorder-independent transport (DIT).

The physicist Philip Anderson introduced the concept of quantum localization in 1958 to explain why diffusion is not observed for spin excitations in impure semiconductors [1]. Localization is a quantum phase transition in which coherent backscattering at disorder centers induces interference effects in—depending on the situation—electrons, spins, phonons, or other quantum excitations. The resulting suppression of transport is especially prevalent in 1D systems [2], which is why researchers working with nanowires are interested in overcoming Anderson localization. A new theoretical study by Nahum Chávez from the Meritorious Autonomous University of Puebla (BUAP), Mexico, and colleagues explores the addition of long-range “hopping” interactions in a 1D disordered system [3]. Their computations of the current through the system show that for weak disorder, Anderson localization shows up roughly as usual, in that disorder hinders transport. The surprise appears when the disorder exceeds a certain value. Then the current shows a notable increase with the disorder, eventually reaching a plateau before it starts to decrease again. Future experiments with trapped atoms in optical lattices and Bose-Einstein condensates (BECs) could probe this predicted hopping-induced delocalization.

The long-range hopping interaction that Chávez and colleagues consider can appear in a variety of instances. An example is a chain of molecules in an optical cavity, where an excitation in one molecule can jump to a distant molecule in the chain through a cavity coupling. The theorist Ugo Fano pointed out that long-range, all-to-all interactions are the source of plasmonic oscillations and superconductivity [4]. In the latter case, it is the phonon-mediated, all-to-all interactions between Cooper pairs at the Fermi surface that are responsible for generating the collective superconducting ground state [5]. In the case considered by Chávez and collegues, a similar ground state occurs, but it is separated from the excited states by a large energy gap. One might assume that the delocalized ground state is “buried” under this gap, unable to mitigate the localization of the excited states. But in a loose metaphor, we can say the ground state rises like a “phantom” to extend the transport probability of the excited states.

To understand this delocalization, we can consider a generic model of excitations, or “excitons.” Under reasonable approximations, the dynamics of excitons is described by a linear chain of $N$ “orbitals” with Anderson disorder. An exciton can occupy one of these orbitals or hop to a nearest-neighbor orbital with a tunneling rate characterized by an energy term $Ω$ . Each orbital has an on-site energy drawn from a random distribution of width $W$ that defines the disorder and discourages the hopping. The excited states have localized wave functions, each of which peaks at a different orbital position and falls exponentially with distance from that peak position. The larger the disorder, the steeper the exponential tails, and the less likely that an excitation can hop to a nearby orbital.

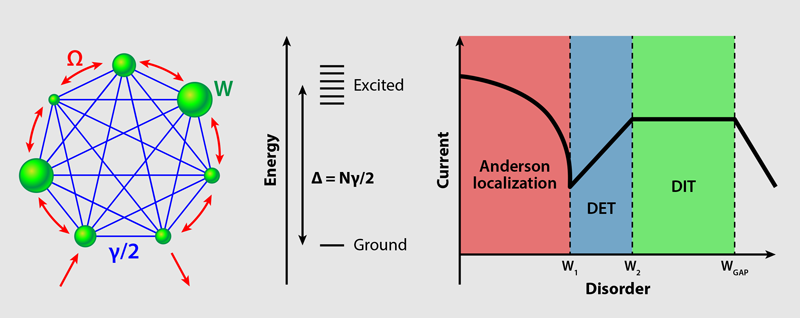
To this generic model, Chávez and co-workers introduce a superimposed effective all-to-all hopping with characteristic energy $𝛾 ∕ 2$ . My student and I previously visualized this type of all-to-all hopping with a “star system” [6], where the ground state $Ψ_{0}$ , with energy $(1 - N) 𝛾 ∕ 2$ , is the fully symmetric superposition of all orbitals, while the $N - 1$ excited states form a band at energy $𝛾 ∕ 2$ (Fig. 1). One might naively think that these (localized) excited states would be safely decoupled from the (delocalized) ground state by the large energy gap of $Δ = N 𝛾 ∕ 2$ . Indeed, localization occurs “almost” as prescribed by Anderson, but the long-range hopping causes the excited states to take on a hybrid character that mixes localized and delocalized states. To understand this hybridization, imagine an $N$ -star system with collective ground state $Ψ_{0}$ , and then add an extra orbital with a localized wave function $Ψ_{N}$ . The new ground state of the system will be approximated by the “bonding” hybrid $Ψ_{0} + Ψ_{N} ∕ \sqrt{N}$ , while the “almost” local excitation is $Ψ_{N} - Ψ_{0} ∕ \sqrt{N}$ . Thus, the strong correlations that constitute the ground state also impose a very weak but unavoidable delocalized floor to each of the excited states. Returning to our metaphor, residual ground states of smaller systems appear as a flat, noisy “phantom” background that can overcome the exponential tails at the extremes of the localized wave functions.

Chávez and colleagues explore this effect by computing the rate of transport, or current, as the disorder is increased. For low disorder, the wave functions are dominated by their relatively broad exponential tails, and the current decreases as disorder increases (Anderson localization). But when the disorder reaches a value of $W_{1}$ , the extremes of the exponential tails plunge under to the “phantom” background. In this disorder-enhanced transport (DET) regime, the wave functions become more spatially extended (more prone to hopping) as the disorder increases. At a higher disorder value of $W_{2}$ , the localization length reaches one lattice unit, and a disorder-independent transport (DIT) occurs exclusively through the “phantom” background. Finally, at disorder above $W_{GAP}$ , the energy gap is closed, and transport again diminishes with increasing disorder.

Since the observables that characterize transport, such as currents, decrease as $1 ∕ N^{2}$ , the delocalization phenomenon might be difficult to tease out of experiments with large $N$ systems. However, there are ways in which the “residual” character of the effect could become observable. On one hand, experiments that try to incorporate long-range couplings in synthetic systems, such as trapped atoms in optical lattices and BECs, have relatively small $N$ . On the other hand, if the all-to-all coupling term becomes reduced to a finite length scale, this scale would break a big system into a sequence of small- $N$ pieces that behave as the described model does. A similar situation may occur in the presence of weak many-body interactions [7]. Since these interactions could be seen as a source of decoherent processes, they would impose a finite coherence length that also breaks the system into pieces with that length [8]. One might also wonder about the effect of long-range couplings in more flexible models of disorder, such as incommensurate potentials that have been implemented experimentally to explore the interplay between localization and many-body effects [9]. Indeed, however weak, the “phantoms” resulting from the ubiquitous collective ground state might still have further unforeseen effects beyond those reported in this paper.

References

P. W. Anderson, “Local moments and localized states,” Rev. Mod. Phys. 50, 191 (1978).
B. Kramer and A. MacKinnon, “Localization: Theory and experiment,” Rep. Prog. Phys. 56, 1469 (1993).
N. C. Chávez et al., “Disorder-enhanced and disorder-independent transport with long-range hopping: Application to molecular chains in optical cavities,” Phys. Rev. Lett. 126, 153201 (2021).
U. Fano, “A common mechanism of collective phenomena,” Rev. Mod. Phys. 64, 313 (1992).
N. H. Chávez et al., “Real and imaginary energy gaps: A comparison between single excitation superradiance and superconductivity and robustness to disorder,” Eur. Phys. J. B 92, 144 (2019).
F. M. Cucchietti and H. M. Pastawski, “Anomalous diffusion in quasi-one-dimensional systems,” Physica A 283, 302 (2000).
M. Schreiber et al., “Observation of many-body localization of interacting fermions in a quasirandom optical lattice,” Science 349, 842 (2015).
J. L. D’Amato and H. M. Pastawski, “Conductance of a disordered linear chain including inelastic scattering events,” Phys. Rev. B 41, 7411 (1990).
P. R. Zangara et al., “Interaction-disorder competition in a spin system evaluated through the Loschmidt echo,” Phys. Rev. B 88, 195106 (2013).

About the Author

Horacio M. Pastawski is a Professor of Physics at the National University of Córdoba and a senior researcher at the Enrique Gaviola Institute of Physics. He graduated from the Instituto Balseiro in Argentina and worked at the Massachusetts Institute of Technology, before joining Córdoba in 1993. He is also a member of the Argentine National Academy of Sciences. He has wide expertise in quantum aspects of molecular electronics and nuclear magnetic resonance. His interests include sonic lasers (SASERs) and adiabatic quantum motors. He develops time-reversal experiments, such as Loschmidt echoes and acoustic time-reversal mirrors, as sensors for quantum dynamical phase transitions, many-body localization, and heterogeneous catalysis.