Shining a Light on Chiral Symmetry Breaking in Graphene
Chirality, or “handedness,” is ubiquitous in nature, from particle and condensed-matter physics to biology and pharmacology. A molecule’s chirality can determine whether it is medicinal or toxic, and the breaking of chiral symmetry is responsible for the mass of the proton in the matter inside and around us [1] (see Focus: Nobel Prize—Particle Physics Gets a Break). Now a team led by Shuyun Zhou of the State Key Laboratory of Low-Dimensional Quantum Physics at Tsinghua University, China, reports measurements on lithium intercalated graphene that directly reveal the signature of “Kekulé” graphene—an elusive phase of graphene in which the chiral symmetry is broken (Fig. 1) [2]. This research highlights the use of intercalated atoms in driving new phases of matter in 2D materials.
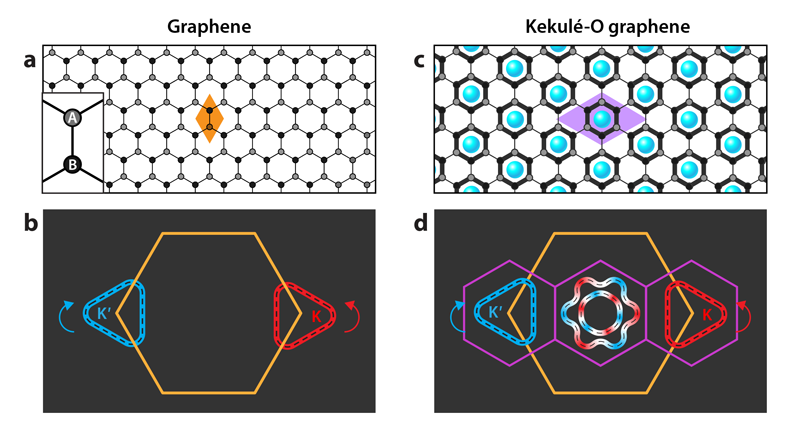
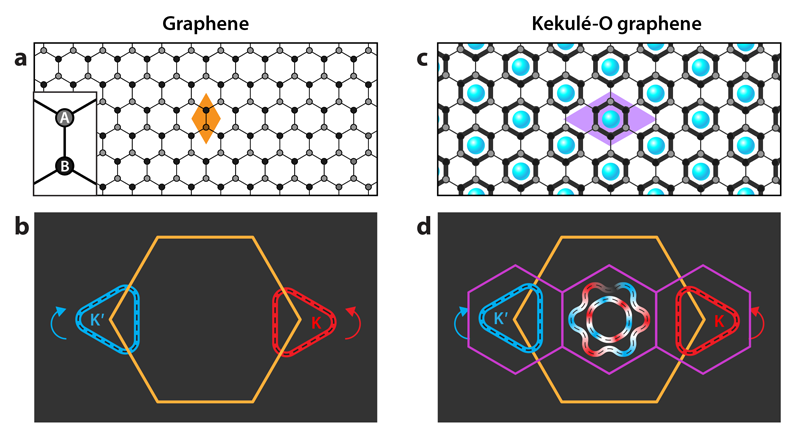
Graphene’s fascinating properties originate from its atomic structure [Fig. 1(a)] [3]. The 2D honeycomb lattice has symmetry that leads to two gapless points in its energy-momentum structure where the conduction and valence bands meet. The electronic bands around these two “Dirac” points have a conical shape, which means that electrons behave as though they’re massless relativistic fermions. In addition to having an intrinsic spin, graphene charge carriers have pseudospin, which is a rotational vector-like quantum property that describes the electronic amplitudes on the two different sublattices [labeled A and B in Fig. 1(a)]. As electrons move through graphene, their pseudospin and direction of motion stay locked together. This is analogous to the relationship between the momentum and intrinsic spin of relativistic fermions predicted by Paul Dirac nearly a century ago and explains why graphene has become an exciting playground for investigating analogs of relativistic quantum effects [3].
Importantly, the locking between pseudospin and momentum is different at the two distinct Dirac points at opposite corners of the Brillouin zone. The pseudospin winds around these two Dirac cones, or “valleys,” with opposite chirality [Fig. 1(b)] [4]. In pristine graphene, chirality is a conserved quantity, so graphene’s charge carriers can be labeled as either purely right or left handed. Any smooth disorder in graphene cannot flip the chirality of the charge carriers [4].
How can chiral symmetry become broken? To answer this question, it’s instructive to look toward the three-dimensional theory of the strong nuclear force, or quantum chromodynamics (QCD). In QCD, up and down quarks also display chirality, and chiral symmetry breaking occurs when right- and left-handed up quarks and down quarks couple together into pairs with opposite chirality. The coupling strength dictates the new composite particle’s mass. If the symmetry breaking occurs through interactions with the quantum vacuum, the symmetry is said to be broken “spontaneously”; if symmetry-breaking terms (in this case, the small quark masses) are already present in the system, the symmetry is said to be broken “explicitly.”
In 2D graphene, the lower dimension allows for additional symmetries and thus multiple ways to break the chiral symmetry [5–8]. One way is to create an imbalance in how electrons occupy the A and B sublattices. Doing so breaks the symmetry between the two lattices and opens an energy gap at the Dirac point proportional to the newly generated mass of the charge carriers [7]. Another way, similar in spirit to chiral symmetry breaking in QCD, directly couples valleys of opposite chirality. This coupling additionally breaks the graphene translational symmetry and leads to a graphene bonding pattern called a “Kekulé distortion,” named after the historical solution of the structure of benzene [Fig. 1(c)] [8].
Direct experimental observations of the Kekulé distortion in graphene are rare [9, 10]. Zhou and colleagues induce a Kekulé distortion by placing lithium atoms between atomic sheets of graphene. The lithium atoms self-assemble into a triangular lattice with an enlarged unit cell and orientation [Fig. 1(c)] that perfectly couple the K and Kʹ valleys, folding them onto each other at the Brillouin zone center [Fig. 1(d)] [11]. When superimposed, the previously quasitriangular Dirac cones hybridize into hexagonal and star-shaped cones [Fig. 1(d)]. Owing to chiral symmetry breaking, the charge carriers described by these new “folded” Dirac cones are right and left handed in equal measure and are no longer chiral [Fig. 1(d)] [4]. The choice of intercalant atom is crucial here: Lithium atoms prefer to sit at the center of graphene hollow sites, while other atomic species prefer the carbon sites. Crucially, the bonding patterns centered at hollow sites (termed Kekulé-O) open energy gaps that generate mass in graphene’s carriers. Bonding patterns centered at carbon sites do not [4].
To directly probe the presence of this new symmetry-broken phase of graphene, Zhou and colleagues combined complementary surface-science techniques. Using atomically resolved scanning tunneling microscopy, they imaged the Kekulé-O bonding pattern of alternating large and small carbon rings. The pattern’s presence verified the translational symmetry breaking of the Kekulé distortion.
To probe the chiral symmetry breaking, the authors used polarization-dependent angle-resolved photoemission spectroscopy (ARPES). Because the intensity of the ARPES signal can be very sensitive to the orientation of the material’s lattice and the polarization of the incident light, the photoemission measurements can also be used to extract the chirality of the electronic wave function [12] (see Viewpoint: Unraveling Electron Chirality in Graphene). By combining several polarization settings of their incident laser source, Zhou and colleagues imaged the chiral symmetry-broken nature of the Kekulé phase of graphene, featuring new Dirac cones of mixed chirality [Fig. 1(d)].
These new results from Zhou and colleagues verify the long-predicted mixed chiral nature of the Kekulé phase of graphene [4–6, 8] and underscore the unique capability of ARPES to probe the topological properties of complex materials. Interestingly, the use of intercalated atoms to open an energy gap in the graphene spectrum and induce the Kekulé phase is similar to the explicit chiral symmetry breaking by up- and down- quark masses in QCD. In nature, explicit symmetry breaking is responsible for roughly 2% of the mass of the proton, with the rest originating from dynamical or spontaneous symmetry breaking. An intriguing question is whether a similar concomitant spontaneous chiral symmetry breaking contributes to the energy gap in Kekulé graphene. Careful measurements of the energy gap while varying the lithium and electron concentration may help answer this question. Superlattices of intercalated atoms thus offer an exciting platform for band engineering new phases in graphene.
References
- Y. Nambu and G. Jona-Lasinio, “Dynamical model of elementary particles based on an analogy with superconductivity. I,” Phys. Rev. 122, 345 (1961).
- C. Bao et al., “Experimental evidence of chiral symmetry breaking in Kekulé-ordered graphene,” Phys. Rev. Lett. 126, 206804 (2021).
- A. H. Castro Neto et al., “The electronic properties of graphene,” Rev. Mod. Phys. 81, 109 (2009).
- M. Koshino et al., “Topological zero modes and Dirac points protected by spatial symmetry and chiral symmetry,” Phys. Rev. B 90, 115207 (2014).
- V. P. Gusynin et al., “AC conductivity of graphene: from tight-binding model to 2 + 1-dimensional quantum electrodynamics,” Intl. J. Mod. Phys. B 21, 4611 (2007).
- I. F. Herbut et al., “Theory of interacting electrons on the honeycomb lattice,” Phys. Rev. B 79, 085116 (2009).
- G. W. Semenoff, “Condensed-matter simulation of a three-dimensional anomaly,” Phys. Rev. Lett. 53, 2449 (1984).
- C.-Y. Hou et al., “Electron fractionalization in two-dimensional graphenelike structures,” Phys. Rev. Lett. 98, 186809 (2007).
- C. Gutiérrez et al., “Imaging chiral symmetry breaking from Kekulé bond order in graphene,” Nat. Phys. 12, 950 (2016).
- S.-Y. Li et al., “Scanning tunneling microscope study of quantum Hall isospin ferromagnetic states in the zero Landau level in a graphene monolayer,” Phys. Rev. B 100, 085437 (2019).
- K. Sugawara et al., “Fabrication of Li-intercalated bilayer graphene,” AIP Adv. 1, 022103 (2011).
- Y. Liu et al., “Visualizing electronic chirality and berry phases in graphene systems using photoemission with circularly polarized light,” Phys. Rev. Lett. 107, 166803 (2011).