Toward Flawless Atom Optics
Since Michelson and Morley’s famous experiment to detect the “luminiferous aether,” optical interferometry has offered valuable tools for studying fundamental physics. Nowadays, cutting-edge applications of the technique include its use as a high-precision ruler for detecting gravitational waves (see Focus: The Moon as a Gravitational-Wave Detector) and as a platform for quantum computing (see Viewpoint: Quantum Leap for Quantum Primacy). But as methods for cooling and controlling atoms have advanced, a new kind of interferometer has become available, in which light waves are replaced by matter waves [1]. Such devices can measure inertial forces with a sensitivity even greater than that of optical interferometers [2] and could reveal new physics beyond the standard model. In a new experiment, Jason Hogan and his colleagues at Stanford University have addressed one of the obstacles that have limited the potential of matter-wave interferometers until now: inefficient coupling between the atoms that constitute the matter waves and the light pulses used to manipulate them [3]. Their technique could lead to matter-wave interferometers sensitive enough to detect fluctuations in Earth’s rotation rate or manifestations of general relativistic effects such as the space-time “torsion” predicted by some alternative theories of gravity.
Whether an interferometer employs light or matter waves, its sensitivity to inertial effects such as rotation depends on the separation between the interferometer arms. In matter-wave interferometers, a large arm separation requires the creation of coherent superpositions of atom momentum states so that the atomic wave function can be delocalized over large distances—typically a few centimeters. Such large arm separations yield strong interferometer sensitivity at the expense of lower interferometer contrast—that is, signal-to-noise ratio. To preserve a high contrast with large arm separations, generally two approaches are used. In both methods, light pulses are used as atom-optics elements to deflect the atomic trajectories by transferring photon momenta to the atoms. The first approach obtains the desired interferometer contrast by increasing the size of the device—as is done, for instance, in the state-of-the-art fountain cold-atom gyroscope used to measure the Sagnac effect with 25 ppm accuracy [4]. The second approach does so by maximizing the momentum transferred by the light pulses to the atoms [5].
Researchers using the latter technique—called large momentum transfer (LMT)—face a problem: the atoms in each arm travel at different velocities, producing a detuning error of the interferometer beams via a differential Doppler shift. The resulting nonidentical light coupling in the two arms induces a contrast loss. To mitigate this problem, conventional LMT atom optics use short, broadband pulses to deflect the atoms. In this approach, the broad bandwidth of the pulses can accommodate for a range of detuning errors but leads to a loss of efficiency and contrast. Hogan and co-workers propose a different approach in which the pulses are also used to control the atom states in a way that automatically corrects the intrinsic detuning error. They show that the frequency detunings of the interferometer beams can be compensated by modulating the atom-light interaction.
Specifically, the team demonstrates a matter-wave interferometer in which strontium atoms oscillate between the 1S0 and 3P1 states. By modulating the amplitude of the coupling between the atoms and the interferometer beams in the 1S0-3P1 optical transition, the researchers generate a set of Floquet states onto which the initial atomic momentum state is projected. The atoms undergo a change in their internal state while simultaneously altering their external state—increasing or decreasing their momenta. This process can be realized with a fidelity close to 100%. How is such a performance possible? We can look at this process from two perspectives.
From the energy point of view one can say that, for a given Doppler detuning of the interferometer beam, the modulation creates a sideband with the frequency required to compensate this detuning. The modulation adds the missing energy needed to fulfil the resonance condition. In other words, the coupling modulation spectrally broadens the light beam over a frequency band covering the Doppler detuning.
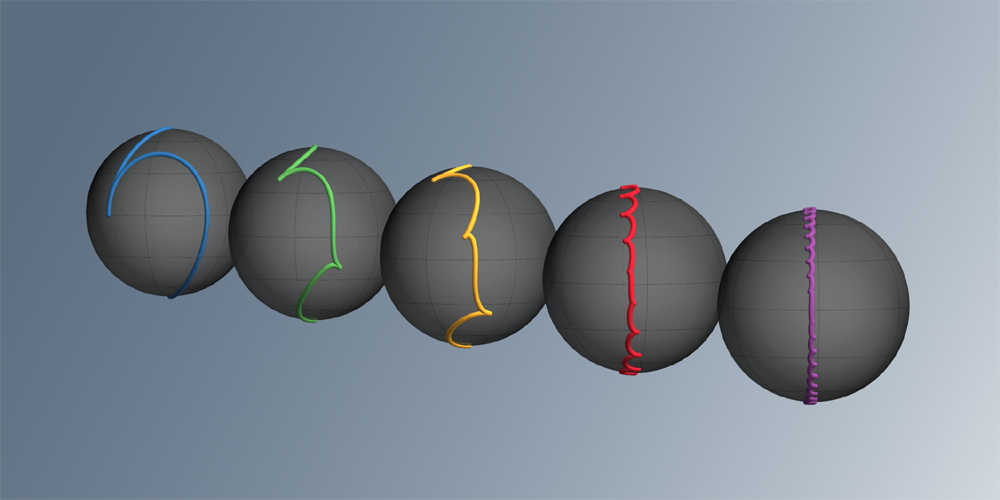
From the quantum-state point of view, by modulating the atom-light coupling, the authors create manifolds of time-dependent dressed states characterized by a well-defined number of modulation energy quanta. Then, by tuning the temporal profile of the coupling, they are able to make the atom-light system evolve from one manifold to another (Fig. 1). Since these manifolds, or Floquet subspaces, correspond to different momenta or propagation velocities of the atoms, one can efficiently transfer a significant amount of photon momenta to the atoms without losing the interferometer contrast. This is the working principle of the Floquet atom optics.
As a result of this process, Hogan and colleagues achieve a large momentum transfer of 400 ħk—setting the state-of-the-art in LMT interferometers—but with a superior ∼10% fringe visibility and a 99.4% efficient population inversion of the interferometer states. Thus, their demonstrated Floquet atom optics provides almost perfect coherent state manipulation. Compared to other currently used techniques, this new method permits a robust, flexible, and easy-to-implement (only three parameters are needed) solution for detuning error correction in large-area matter-wave interferometers. In addition, engineering the atom-light coupling in this way might offer new perspectives in, for instance, controlling momentum transfer to the atoms even when they are trapped in modulated potentials [6], engineering decoherence-free subspaces for quantum information processing [7], and performing quantum simulation [8].
References
- Ch. J. Bordé, “Atomic interferometry with internal state labelling,” Phys. Lett. A 140, 10 (1989).
- A Peters et al., “High-precision gravity measurements using atom interferometry,” Metrologia 38, 25 (2001).
- T. Wilkason et al., “Atom interferometry with Floquet atom optics,” Phys. Rev. Lett. 129, 183202 (2022).
- R. Gautier et al., “Accurate measurement of the Sagnac effect for matter waves,” Sci. Adv. 8 (2022).
- J. M. McGuirk et al., “Large area light-pulse atom interferometry,” Phys. Rev. Lett. 85, 4498 (2000).
- I. Bouchoule et al., “Limitations of the modulation method to smooth wire-guide roughness,” Phys. Rev. A 77, 023624 (2008).
- C. Chen et al., “Floquet control of quantum dissipation in spin chains,” Phys. Rev. A 91, 052122 (2015).
- N. Goldman et al., “Topological quantum matter with ultracold gases in optical lattices,” Nat. Phys. 12, 639 (2016).