Topological Magnetism Turns Elementary

Helen Walker

Viewpoint

Topological Magnetism Turns Elementary

ISIS Neutron and Muon Source, Rutherford Appleton Laboratory, Didcot, United Kingdom

March 2, 2022• Physics 15, 30

Neutron scattering experiments provide the evidence of massless spin waves called Dirac magnons in a single-element magnetic crystal, offering a new window into topological magnetism.

Figure caption — **Figure 1:** The magnon spectrum of gadolinium exhibits topological features. As shown in gadolinium’s Brillouin zone (left), there exists a nodal line (black), which extends along the $l$ direction through the $K$ point. The Dirac crossings along this line have an asymmetric pattern, represented by the color shading of the Dirac cones (right). Additionally, the cones flatten into a nodal plane at $l = 1 ∕ 2$ (green).

Despite appearing to be disparate fields, high-energy particle physics and condensed-matter physics have a long history of successfully contributing to each other. For example, Philip Anderson’s work on superconductivity and symmetry breaking in 1963 [1] led to the development of the Higgs mechanism, which explains how particles acquire mass. More recently, concepts from particle physics have entered the realm of condensed matter with the observation that electrons in graphene move as if they were massless, obeying the relativistic Dirac equation for fermions [2]. This Dirac behavior has been observed in collective magnetic spin oscillations, or magnons. Owing to their massless property, Dirac magnons can propagate over longer distances without dissipating energy as heat—a potentially useful property in spintronics. Prior detections of Dirac magnons were made in 2D ferromagnets [3, 4] and 3D antiferromagnets [5]. Now, Allen Scheie from Oak Ridge National Laboratory, Tennessee, and colleagues have observed Dirac magnons in pure elemental gadolinium, a 3D ferromagnet [6, 7]. The practically disorder-free crystal structure of gadolinium allows the researchers to obtain clean magnon spectra. The results reveal topological phases in gadolinium and suggest that other elemental magnets may host exotic topological states.

The telltale signature of Dirac particles is a cone-shaped feature in the band structure. In the case of graphene and other materials, such as topological insulators, the Dirac cone is observable as a linear crossing of the conduction and valence electronic bands. Near the crossing point, the electrons can be described by the Dirac equation, which was originally derived for the case of massless fermions. However, Dirac physics is not limited to fermions. Experiments have shown that bosons, such as magnons, plasmons, and phonons, can have Dirac crossings in their band structures. Magnons are quasiparticles describing quantized disturbances of the magnetic structure. These disturbances propagate as spin waves in roughly the same way as phonon excitations propagate as displacement waves within the crystal lattice. Dirac crossings of magnon bands have previously been observed in a number of 2D honeycomb ferromagnets ( ${CrX}_{3}$ and ${CoTiO}_{3}$ [3, 4]) and in the 3D cubic antiferromagnet ${Cu}_{3} {TeO}_{6}$ [5]. Scheie and co-workers have now provided a full characterization of the Dirac magnons in a single-element material, gadolinium (Gd).

Gadolinium is a rare-Earth magnetic material that is used in nuclear-power generation, medical imaging, magnetic refrigeration, and solid oxide fuel cells. It is metallic, crystallizes in a hexagonal-close-packed structure (a simple 3D bipartite lattice), and becomes ferromagnetic at a critical temperature of 293 K. The material has near-perfect isotropy and vanishing spin-orbit coupling, making it a simple model system for studying magnon behavior.

Scheie and colleagues studied Gd using inelastic neutron scattering at the Spallation Neutron Source at Oak Ridge National Laboratory. In this technique, neutrons, which have magnetic moments, create and annihilate magnons when they scatter from a Gd crystal. By measuring the energy lost by the neutrons during the scattering process, the researchers were able to identify magnon modes over all directions within the crystal lattice, going beyond previous measurements that focused on only certain lattice directions [8].

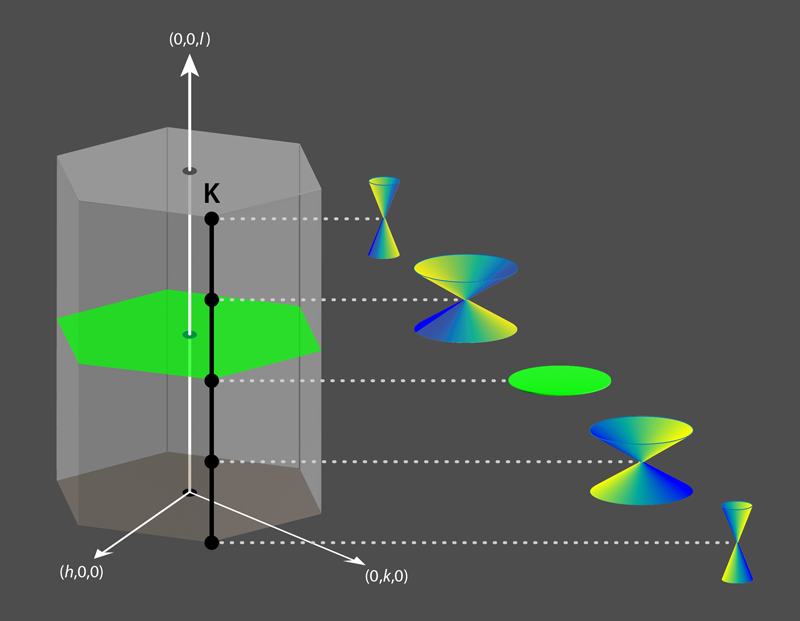
The data were plotted in the Brillouin zone (BZ), the primitive unit cell in momentum space, which is a hexagonal prism in the case of Gd (Fig. 1). Points in the BZ are specified by the indices ( $h, k, l$ ), which are normalized with respect to the lattice spacing. Previous work had detected a linear Dirac crossing at the $K$ point (1/3, 1/3 ,0), but the fuller picture provided by Scheie and colleagues reveals that the crossing is degenerate, extending along all values of the index $l$ . Such a feature is called a nodal line.

The nodal line along $l$ shows an anisotropic intensity pattern; in other words, the neutron scattering is greater on one side of the Dirac cone than on the other. The direction of this modulation is inverted for energies above and below the crossing point. This winding behavior is the signature of a topological phase called a Berry phase. The topological character of this phase is determined by Gd’s symmetries, which include both inversion and time-reversal symmetry. These same symmetries protect the magnon nodal lines from disorder that could affect the crossing. The calculations by Scheie and co-workers suggest that the nodal lines produce a topological surface magnon mode that is distinct from the bulk magnon modes. While they could not directly prove this conclusion, as neutron scattering measurements are not sensitive to surface modes, the team’s modeling is consistent with the data.

Moving along the nodal line, the Dirac cone flattens at $l = 1 ∕ 2$ into a nodal plane—a degeneracy in the modes at all $h$ and $k$ . Electronic nodal planes were predicted in semimetals and have been observed at the Fermi surface of the topological material MnSi, but the team’s experiments provide the first experimental observation of a magnonic nodal plane. This magnon equivalent of an electronic nodal plane expands the set of analogies between topological magnets and topological electronic systems, which have proven very fruitful in extending knowledge of one system onto the other. The consequences of the nodal plane remain open to future study, with potential for topological magnon bands beyond Dirac cones.

Gadolinium is not the only elemental, hexagonal-close-packed ferromagnet, as similar properties are found in other rare-Earth metals, such as terbium and dysprosium, and in hexagonal cobalt. Given the intrinsic connection between symmetry and topology, these related magnets might host similar magnon features, but their topology could be different because their magnetic interactions are more anisotropic than those of Gd. Through theoretical modeling, Scheie and his colleagues also explored the effect anisotropies might have [7]. For example, they looked at the antisymmetric Dzyaloshinskii-Moriya exchange interaction, which breaks time-reversal symmetry. They found that this interaction lifts the nodal plane degeneracy while leaving the $l = 1 ∕ 2$ nodal lines, potentially resulting in surface magnon modes with a preferred handedness, or chirality. Such chiral modes would depend on spin orientation and could be tuned with a magnetic field, but they could also be suppressed by effects like spin-orbit coupling. Further theoretical modeling is necessary to determine whether chiral surface modes could be observed. But gadolinium has opened the door to a new realm of possibilities in topological magnetism.

References

P. W. Anderson, “Plasmons, Gauge Invariance, and Mass,” Phys. Rev. 130, 439 (1963).
A. H. Castro Neto et al., “The electronic properties of graphene,” Rev. Mod. Phys. 81, 109 (2009).
L. Chen et al., “Topological spin excitations in honeycomb ferromagnet ${CrI}_{3}$ ,” Phys. Rev. X 8, 041028 (2018); “Topological spin excitations in honeycomb ferromagnet ${CrI}_{3}$ ,” 8, 041028 (2018).
B. Yuan et al., “Dirac magnons in a honeycomb lattice quantum XY magnet ${CoTiO}_{3}$ ,” Phys. Rev. X 10, 011062 (2020); M. Elliot et al., “Order-by-disorder from bond-dependent exchange and intensity signature of nodal quasiparticles in a honeycomb cobaltate,” Nat. Commun. 12, 3936 (2021).
W. Yao et al., “Topological spin excitations in a three-dimensional antiferromagnet,” Nat. Phys. 14, 1011 (2018); P. Bao, D. Y. Tsao, “Representation of multiple objects in macaque category-selective areas,” Nat. Commun. 9, 1774 (2018).
A. Scheie et al., “Dirac magnons, nodal lines, and nodal plane in elemental gadolinium,” Phys. Rev. Lett. 128, 097201 (2022).
A. Scheie et al., “Spin-exchange Hamiltonian and topological degeneracies in elemental gadolinium,” Phys. Rev. B 105, 104402 (2022).
W. C. Koehler et al., “Spin-Wave Dispersion Relations in Gadolinium,” Phys. Rev. Lett. 24, 16 (1970).

About the Author

Helen Walker is a staff scientist at the ISIS Neutron and Muon Source in the UK, specializing in exploring the collective dynamics of functional materials. She holds an undergraduate degree in natural sciences from the University of Cambridge and a Ph.D. in experimental condensed-matter physics from University College London. Prior to becoming a neutron scientist, she worked at the European Synchrotron Radiation Facility in France and at PETRA III at DESY, Germany. Her research interests include magnetism in metal organic frameworks and structure-dynamics-property relations in barocalorics. She won the ESRF Young Scientist of the Year Award in 2011 and is currently one of the Foundation Future Leaders at the Foundation for Science and Technology in the UK.