Angle-Preserving Transformations Give Rigidity Transitions a New Twist

Jen Schwarz; Silke Henkes

Viewpoint

Angle-Preserving Transformations Give Rigidity Transitions a New Twist

¹Department of Physics, Syracuse University, Syracuse, NY
²Institute of Physics, Leiden University, Leiden, Netherlands

January 2, 2024• Physics 17, 1

New theoretical work explores the onset of rigidity in granular materials and other disordered systems by mapping out the edges of rigid regions.

Figure caption — **Figure 1:** The interfaces of rigid clusters in an amorphous system evolve according to a framework known as Schramm-Loewner theory. At the rigidification transition, these clusters are consistently described by universal parameters including the universal diffusion constant $𝜅$ , the clusters’ fractal dimension $d_{f}$ , and correlation length exponent $𝜈$ . This theory treats the edges of clusters as a family of curves that are conformally invariant. Researchers show that it applies to a mechanical percolation transition, opening the way to a new understanding of microstructure in other jamming transitions.

Phase transitions are a common part of our daily lives. Many of them are intuitive: water transforms into steam or ice, birds spontaneously form a flock, and random piles of marbles suddenly jam together into a solid. Possibly the most basic phase transition, however, is a more abstract version called connectivity percolation (CP). In systems displaying CP, individual units such as persons or polymers are mapped by their contacts—or connectors—to a graph consisting of nodes and edges. As the number of connectors increases, the system switches from being disconnected (filled with small, separate clusters) to being connected (spanned by one large cluster). This connectivity phase transition is commonly seen in polymer solutions and pandemic spreading, but researchers have also used the percolation perspective to describe the onset of mechanical rigidity in disordered systems, otherwise known as rigidity percolation (RP). A study now shows that a tried-and-true mathematical physics approach, applied earlier to CP, captures new universal parameters that describe RP [1]. The work could lead to a better understanding of the microstructure connections that produce rigidity in disordered systems, such as grain packings and living tissues.

A stable mound of marbles is rigid in the sense that if you gently push on one of the marbles, the mound does not collapse. In other words, that marble is part of a rigid cluster—a group of marbles that resists deformation of its collective arrangement. We can imagine how this stability came about: marbles are piled onto the mound, locking down the ones below within small, separate clusters. As more marbles are added, the clusters become larger (the rigidity percolates) until the entire mound is locked in place. In many ways, this RP resembles the process that produces a spanning cluster in CP. Still, theorists have long believed that, despite their similarities, CP and RP are fundamentally different types of phase transitions.

The argument that CP and RP are different is based, in part, on the shapes of their clusters. The complexity of these shapes can often be characterized by a geometric parameter called the fractal dimension. As one identifies a spanning cluster, one can extract its fractal dimension numerically from the number of edges in the cluster as a function of system size. This approach works in all dimensions. However, for two dimensions, researchers have used several techniques including conformal field theory (CFT) to analytically compute the fractal dimension of spanning clusters in CP [2]. For RP, the situation is less straightforward. That’s because for some cases, numerically generated RP clusters are nonfractal, while in other cases they are fractal but with different scaling behavior from CP [3–5].

Despite these differences, recent efforts have delved further into RP with the aim of extending the techniques used in CP. The hope is that the already-thorough understanding of CP can provide a better understanding of the more mysterious RP. In one contribution, with several colleagues, we recently introduced the concept of frictional RP for real frictional particles, such as marbles, in two dimensions. Using a pebble algorithm, our work identified rigid clusters in simulations [6], in experiments, and in a lattice model. We established that the exponents that describe the scaling behavior within the system are different for standard RP and frictional RP, thereby making the RP story more intricate [7]. In another contribution, Nina Javerzat, now at the International School for Advanced Studies (SISSA) in Italy, and Mehdi Bouzid, now with the French National Center for Scientific Research (CNRS), confirmed that the RP transition on a triangular lattice is indeed continuous and exhibits both global and local conformal invariance [8]. Conformal invariance refers to a system whose governing equations remain intact under any continuous mapping that preserves angles from one 2D grid to another. This invariance is much more stringent than the typical scale, translational, and rotational invariance that applies to continuous phase transitions [8].

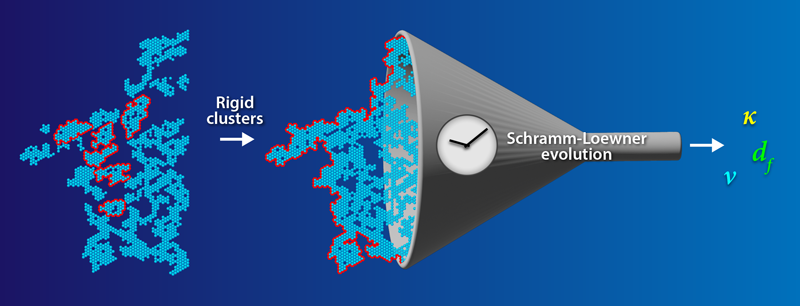
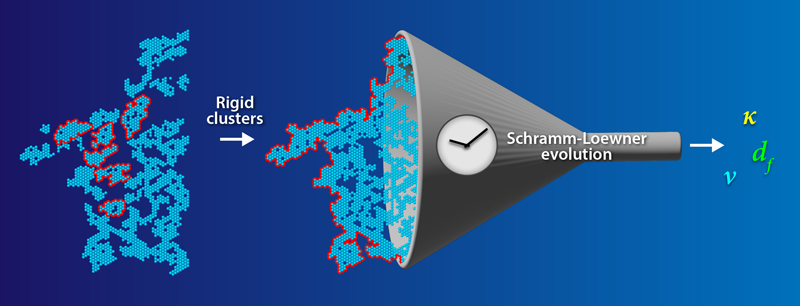
These new insights opened the field of RP to the full spectrum of CFT techniques. In the new work, Javerzat uses an elegant technique called Schramm-Loewner evolution (SLE) to directly probe the shape of spanning rigid clusters [1] (Fig. 1). This technique involves conformally mapping the path formed by the perimeter of a spanning rigid cluster to the trajectory of a time-dependent process.

To perform this mapping, Javerzat generated numerous rigid clusters on a triangular lattice that spanned the region between the top and bottom of the system. She then treated each cluster’s border as an instantaneous step in a random process in time: in other words, each border is a random curve that evolves according to equations defined in the SLE technique. In this way, the random curves are reparameterized by a series of conformal maps related by a driving function and a universal diffusion constant $𝜅$ . The diffusion constant is then used to derive the fractal dimension $d_{f}$ and the correlation length exponent $𝜈$ of the clusters. For her triangular system with rigid clusters, Javerzat computed a diffusion constant of $𝜅$ = 2.8, consistent with the measured fractal dimension of RP. In CP, $𝜅$ has a value of 6 [9]. Javerzat’s calculations demonstrate that, like CP, RP is continuous at the transition. The difference between the two universal diffusion constants suggests that CP and RP are nonetheless distinct types of transitions or distinct universality classes.

However, Javerzat points out that for minimally rigid clusters that do not have any redundant edges, the phase transition could, in principle, have the same universal diffusion constant as that of CP. This idea partly builds on work that created a process of growing minimally rigid spanning clusters for frictional particles [7]. This growth is very similar to spanning minimally rigid clusters of frictionless particles and even for the simpler spanning clusters of CP. Our results suggested a type of superuniversality for clusters right at these transitions.

Using techniques from SLE and CFT to analyze rigidity transitions in two dimensions opens exciting new avenues from which to understand how mechanical stability arises in random structures. In particular, it would be interesting to find out if the frictional rigid clusters in jamming map to frictionless rigid clusters that evolve according to SLE but with a different $𝜅$ than their frictionless RP counterpart. Moreover, debates have long been waged over the transitions exhibited by different percolation models [10, 11]. Whether these transitions are continuous or discontinuous could be resolved more quickly in two dimensions using such techniques.

References

N. Javerzat, “Schramm-Loewner evolution in 2D rigidity percolation,” Phys. Rev. Lett. 132, 018201 (2024).
J. L. Cardy, “Conformal invariance,” Phase Transitions and Critical Phenomena, edited by C. Domb et al. (Academic Press, London, UK, 1987), Vol. 11, p. 55.
D. J. Jacobs and M. F. Thorpe, “Generic rigidity percolation: The pebble game,” Phys. Rev. Lett. 75, 4051 (1995).
C. Moukarzel and P. M. Duxbury, “Comparison of rigidity and connectivity percolation in two dimensions,” Phys. Rev. E 59, 2614 (1999).
M. V. Chubynsky and M. F. Thorpe, “Algorithms for three-dimensional rigidity analysis and a first-order percolation transition,” Phys. Rev. E 76, 041135 (2007).
S. Henkes et al., “Rigid cluster decomposition reveals criticality in frictional jamming,” Phys. Rev. Lett. 116, 028301 (2016).
K. Liu et al., “Frictional rigidity percolation: A new universality class and its superuniversal connections through minimal rigidity proliferation,” Phys. Rev. X 9, 021006 (2019).
N. Javerzat and M. Bouzid, “Evidences of conformal invariance in 2D rigidity percolation,” Phys. Rev. Lett. 130, 268201 (2023).
S. Smirnov, “Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits,” C. R. Seances Acad. Sci., Ser. 1 333, 239 (2001).
L. Cao and J. M. Schwarz, “Correlated percolation and tricriticality,” Phys. Rev. E 86, 061131 (2012).
D. Achlioptas et al., “Explosive percolation in random networks,” Science 323, 1453 (2009).

About the Authors

Jen Schwarz is a professor of physics at Syracuse University, New York, and a fellow of the APS. Her theoretical physics research group studies percolation transitions, rigidity transitions, and shape instabilities in living and nonliving matter ranging from such systems as granular packings to fiber networks to brain organoids. In collaboration with Silke Henkes, David Quint, and Yaouen Fily, she introduced frictional rigidity percolation, a new class of rigidity percolation for frictional granular packings in 2016. Since then, the researchers have continued to develop the theory along with experimentalist Karen Daniels and others.

Silke Henkes is an associate professor of physics at Leiden University, Netherlands. Her research group focuses on the physics of active materials, or how a collection of independently moving agents work together collectively, with the agents spanning from particles in granular materials to cells in epithelial cell sheets. Prior to arriving at Leiden University in 2022, she held lecturer positions at the University of Aberdeen and the University of Bristol, both in the UK. In collaboration with Jen Schwarz, David Quint, and Yaouen Fily, she introduced frictional rigidity percolation, a new class of rigidity percolation for frictional granular packings in 2016. Since then, the researchers have continued to develop the theory along with experimentalist Karen Daniels and others.