Synthesizing New 3D Materials by Twisting
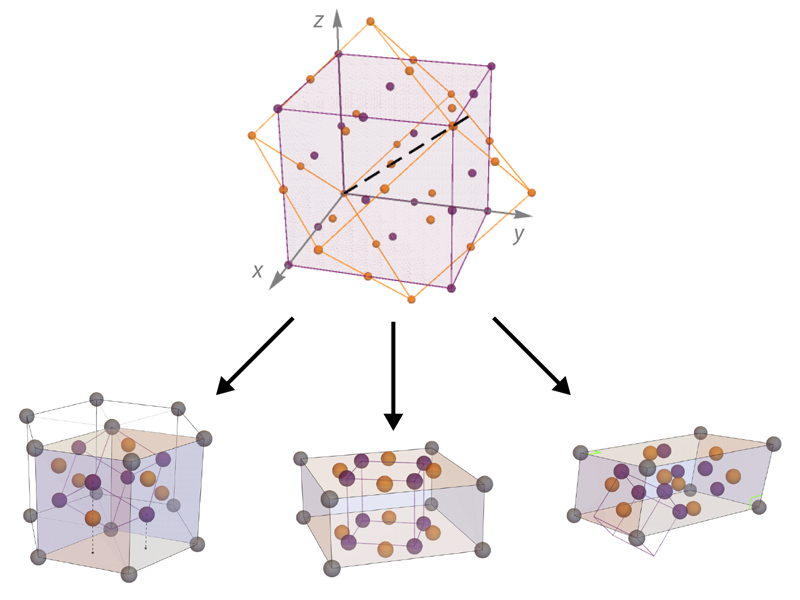
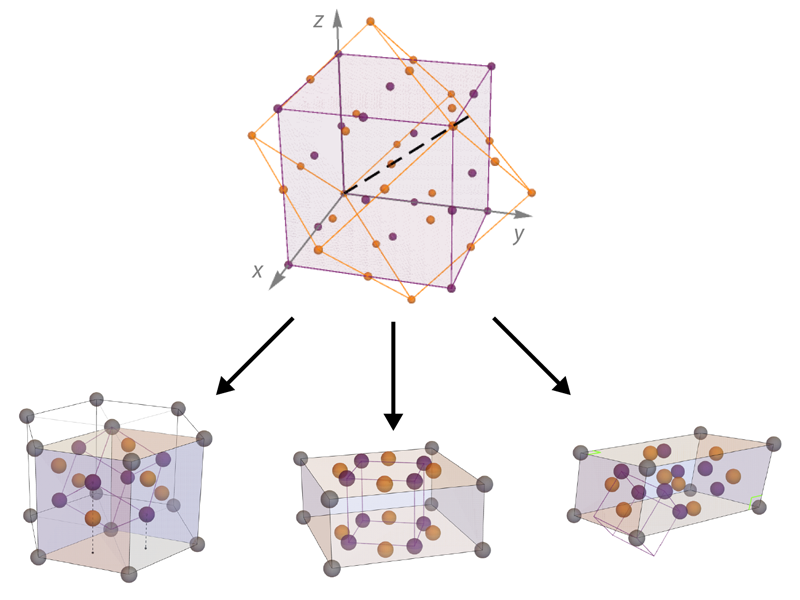
When two identical periodic lattices overlap in space, with one twisted at an angle relative to the other, they form moiré lattices. The best-known examples are formed from stacked and rotated 2D sheets. These structures can possess fascinating properties not seen in their component layers. Twisted bilayer graphene, for example, can exhibit superconductor and Mott insulator behavior [1, 2]. Ce Wang of Tongji University in China and his colleagues now propose how to construct a 3D moiré lattice using two cubic optical lattices hosting ultracold atoms [3]. The researchers mathematically describe how two simple periodic structures, twisted relative to each other, can lead to 3D optical moiré patterns (Fig. 1). The result is a crystal-like structure with emergent properties that differ from those of the underlying simple lattices. The researchers show that adjusting the twisting axes and angles leads to various crystalline symmetries, enabling the exploration of diverse material properties.
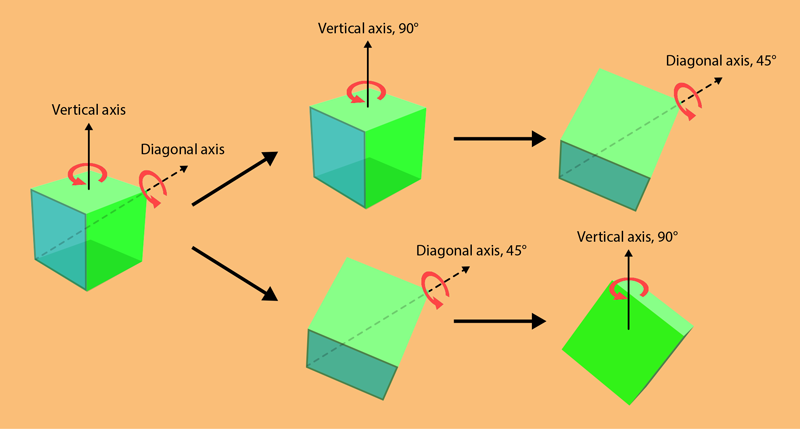
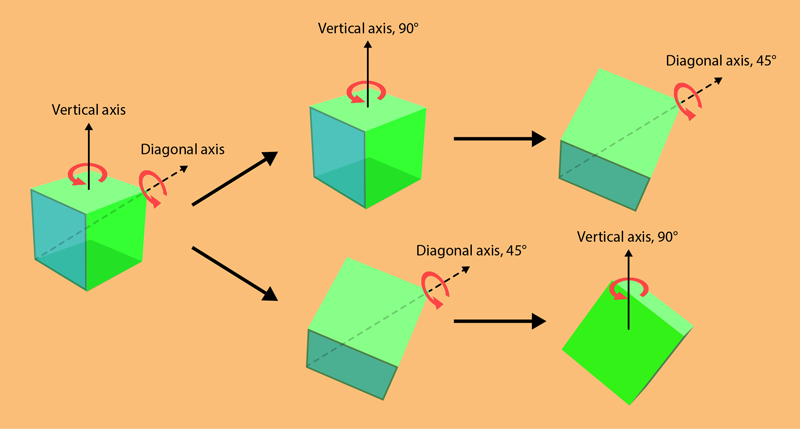
In the past five years, researchers have experimentally demonstrated the moiré lattice concept in optical [4–7] and cold-atom [8] systems. These demonstrations show the possibility of extending the concept from 2D into 3D. One of the most intriguing aspects of 3D moiré patterns is their non-Abelian rotation: The order in which you rotate the lattice significantly affects the final structure. This property contrasts with 2D systems, in which rotating an object by one angle and then another yields the same result regardless of the order.
Non-Abelian rotation can be visualized by rotating a cube. Turning the cube 90° around one axis and then 45° around another axis (Fig. 2) results in a different orientation than if you had performed those rotations in the reverse order. Now, suppose you have two cubic lattices, one fixed and the other twisted about its axis (Fig. 2). Combining the two—creating 3D moiré lattices—will obviously lead to different structures, depending on which rotation happens first. This complexity allows for a richer variety of crystalline arrangements and, consequently, of material properties. Exploiting this non-Abelianism, therefore, offers researchers a powerful tool to “synthesize” new materials by manipulating existing ones and to study how different crystalline symmetries interact with atoms, photons, and electrons.
Wang and colleagues’ mathematical demonstration of the range of 3D moiré crystal structures that can be realized offers a fascinating look into the outcomes that non-Abelian physics makes possible. Notable among these is a feature exclusive to 3D crystals: the presence of Weyl points [9]. Weyl points are the intersections of linearly dispersing energy bands similar to the Dirac points that arise in 2D crystals. Synthesizing a material whose energy band structure contains Weyl points opens doors to exploring a variety of intriguing phenomena such as topologically protected surface states and chiral anomalies. In recent years, researchers have successfully designed various intricate 3D structures to generate Weyl points [9, 10]. Surprisingly, Wang and colleagues’ numerical work reveals that by simply twisting two cubic lattices, the resultant 3D moiré crystals host many Weyl points and nodal lines. This result shows that 3D moiré lattices represent an alternative route to creating topological materials and correspondingly exotic states.
Wang and colleagues propose to implement 3D moiré lattices in the context of ultracold atoms, where these arrangements have the potential to enhance the exploration of diverse crystalline symmetries and their associated nontrivial band structures. However, the concept can be extended to other fields such as optics and acoustics, where it might bring many other new possibilities. One intriguing avenue for further investigation is the study of 3D moiré crystals under nonperiodic, or incommensurate, phases—that is, in crystals that do not possess the property of translational invariance. Note that Wang’s current study only considers the periodic, or commensurate, phase. An immediate question concerning 3D nonperiodic moiré crystals is whether localized wave packets, confined within the 3D space, exist. The existence of such wave packets in 2D is already well established [4, 6]. In a 3D system, because three twisting angles can be tuned separately, one can imagine localizing a wave in one plane while controlling its propagation in another specific, tunable direction. This could offer a unique approach to wave localization (creating a totally novel cavity) and subsequent access to it (novel waveguiding).
Additionally, it would be interesting to explore how nonlinear phenomena that might occur in a lattice with a 3D moiré structure differ from their 2D counterparts. For example, optical Kerr nonlinearity or two-body interactions in Bose-Einstein condensates could bring about new properties like the formation of higher-dimensional solitons controlled by the twisting [11]. Breakthroughs, both experimental and theoretical, in these intriguing directions involving 3D moiré lattices are anticipated in the near future.
References
- Y. Cao et al., “Correlated insulator behaviour at half-filling in magic-angle graphene superlattices,” Nature 556, 80 (2018).
- Y. Cao et al., “Unconventional superconductivity in magic-angle graphene superlattices,” Nature 556, 43 (2018).
- C. Wang et al., “Three-dimensional moiré crystal in ultracold atomic gases,” Phys. Rev. Lett. 133, 163401 (2024).
- P. Wang et al., “Localization and delocalization of light in photonic moiré lattices,” Nature 577, 42 (2019).
- G. Hu et al., “Topological polaritons and photonic magic angles in twisted 𝛼-MoO3 bilayers,” Nature 582, 209 (2020).
- X.-R. Mao et al., “Magic-angle lasers in nanostructured moiré superlattice,” Nat. Nanotechnol. 16, 1099 (2021).
- W. Wang et al., “Moiré fringe induced gauge field in photonics,” Phys. Rev. Lett. 125, 203901 (2020).
- Z. Meng et al., “Atomic Bose–Einstein condensate in twisted-bilayer optical lattices,” Nature 615, 231 (2023).
- A. Vishwanath, “Where the Weyl things are,” Physics 8, 84 (2015).
- L. Lu et al., “Weyl points and line nodes in gyroid photonic crystals,” Nat. Photonics 7, 294 (2013).
- Q. Fu et al., “Optical soliton formation controlled by angle twisting in photonic moiré lattices,” Nat. Photonics 14, 663 (2020).