Water Can Host Topological Waves
When wind or other movements perturb a calm water surface, parcels of fluid are displaced in three dimensions from their equilibrium positions. This perturbation propagates across the water surface as visible ripples or waves. These surface water waves form familiar patterns with linear and circular shapes, but new work suggests that more exotic patterns are possible and include other intriguing topological features. Daria Smirnova, Franco Nori, and Konstantin Bliokh of RIKEN in Japan now explore systematically how a zoo of topological wave structures can emerge in these water waves [1]. The work describes how these structures, which have previously been observed in optical, elastic, and quantum systems, could be implemented in straightforward experiments. Water waves might thus offer a practical platform for probing universal topological wave phenomena.
Numerous physical systems—from classical electromagnetic fields to quantum particle fields—exhibit oscillating wave behavior [2]. Specific settings exist, both in nature and in artificial systems, where these waves form patterns with holes, loops, and other distinct topological characteristics, often referred to as topological wave structures [3].
Topological structures form the basis of many intriguing phenomena, for example, the quantum Hall effect and topological superconductivity. The study of topology has revolutionized our understanding of different material systems, as recognized by the 2016 Nobel Prize. Among possible applications, topological structures are emerging as a robust format for storing quantum information for a quantum computer (see Viewpoint: A Roadmap for a Scalable Topological Quantum Computer).
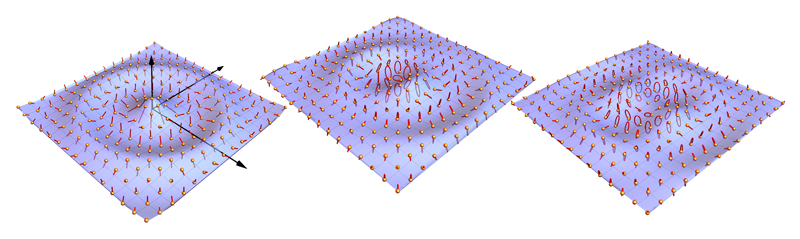
Smirnova and co-workers focus on the possibility that topological structures could emerge in water waves, specifically in the oscillatory motion of water particles on the surface [1]. Their approach is based on a common method for generating topological waves: combine a suitable set of plane waves, whose interference leads to wave field arrangements that display nontrivial topological structures (Fig. 1 shows a typical interference pattern of two water waves). The researchers first imagine combining an infinite set of plane waves emanating outward in all directions from a center point. These waves are chosen so that their oscillations are delayed in a sequential manner. The researchers show analytically that the interference between these waves creates a topological structure called a phase vortex. In the case of scalar waves, a phase vortex is a zero-amplitude point of the oscillating field. If one draws a circle (or any closed line) around this point, one finds the relative shift between waves oscillations equals an integer number of wave periods. That integer is called the topological charge, and Smirnova and colleagues find that this charge is related to the angular momentum carried by the wave.
Because these are three-dimensional (3D) waves, the wave equation dictates that their in-plane displacement components also carry phase vortices. Smirnova and colleagues show that the 3D profile of such water waves exhibits patterns that depend on the topological charge, with peaks and valleys at symmetric angular positions (Fig. 2), rotating in time [4, 5]. This rotation is not the same as a whirlpool-like hydrodynamical vortex, where a steady flow of water traces the vortex. Instead, a slow drift emerges because of the orbital component of the angular momentum density. Locally, particles form closed elliptical trajectories that are reminiscent of the path traced out by the electric field in elliptical polarization. Their cycle-averaged angular momentum, perpendicular to the ellipse, represents the spin density of the wave field [6].
In a simpler configuration with only three waves, Smirnova and colleagues’ interference scheme leads to a periodic arrangement of particle oscillations exhibiting other topological structures called skyrmion and meron lattices [7]. The skyrmion emerges when—for each unit cell in the lattice—the instantaneous displacement vectors point in all possible spatial directions. The same texture characterizes the states forming the energy bands of Chern insulators and underlies the quantum Hall effect [8]. In the same configuration, the 3D spin density of the wave field is arranged in zones that cover only half of all possible directions, leading to structures known as merons.
The recipe from Smirnova, Nori, and Bliokh yields topological effects that could be directly observable in a water tank, without relying on indirect detection methods that are necessary in other fields such as optics or acoustics. Probing topological wave structures in a simple and controllable system like water waves opens opportunities for implementing complex wave configurations in accessible laboratory settings [9]. Here, the amplitude, phase, spin, and orbital angular momentum of the evolving waves can be directly observed and linked to mechanical properties of water.
The study of waves in optics and condensed matter has revealed a range of topological structures, such as vortices, skyrmions, and merons, whose observation in water waves has just started. However, water waves might one day be the medium of discovery, facilitated by the superior controllability of these wave systems. Studying complex topological waves in water tanks, by creating and combining multiple waves through controlled delays in their oscillations, could lead to the discovery of universal phenomena. Eventually, such waterborne findings could be replicable in other wave systems.
References
- D. A. Smirnova et al., “Water-wave vortices and skyrmions,” Phys. Rev. Lett. 132, 054003 (2024).
- M. R. Dennis, Topological singularities in wave fields, diss., University of Bristol (2001).
- J. Harris et al., “Structured quantum waves,” Nat. Phys. 11, 629 (2015).
- M. F. Picardi et al., “Angular momenta, helicity, and other properties of dielectric-fiber and metallic-wire modes,” Optica 5, 1016 (2018).
- K. Y. Bliokh, “Elastic spin and orbital angular momenta,” Phys. Rev. Lett. 129, 204303 (2022).
- K. Y. Bliokh et al., “Field theory spin and momentum in water waves,” Sci. Adv. 8, eabm1295 (2022).
- X. Lei et al., “Photonic spin lattices: Symmetry constraints for skyrmion and meron topologies,” Phys. Rev. Lett. 127, 237403 (2021).
- K. von Klitzing et al., “40 years of the quantum Hall effect,” Nat. Rev. Phys. 2, 397 (2020).
- N. Francois et al., “Wave-based liquid-interface metamaterials,” Nat. Commun. 8, 14325 (2017).