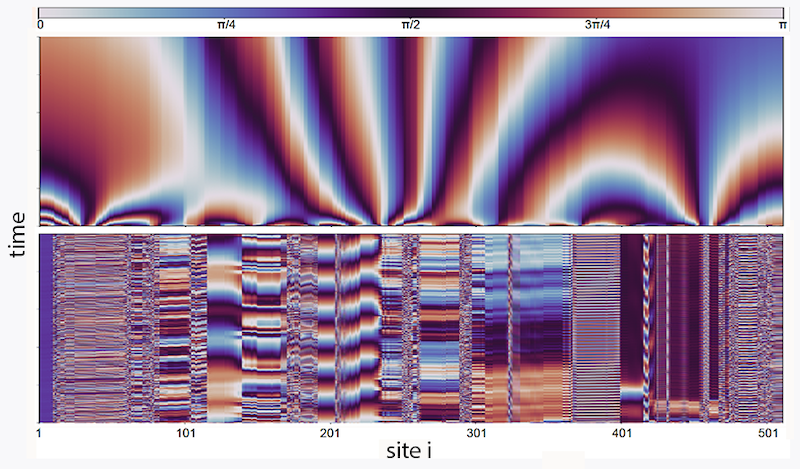
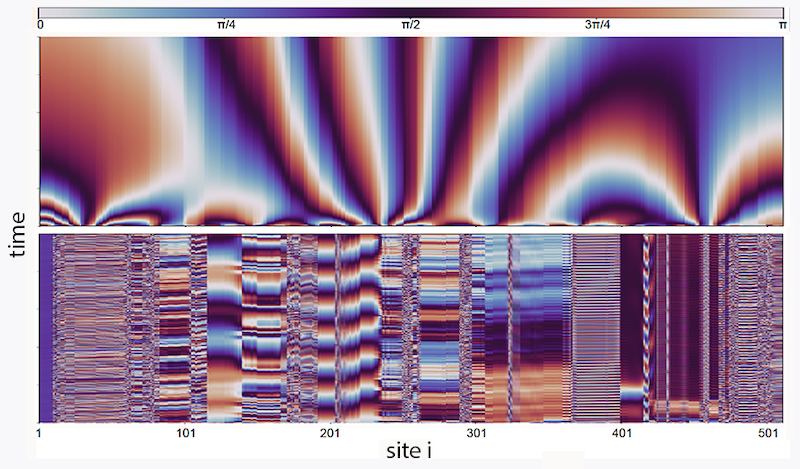
Nonreciprocal Frustration Meets Geometrical Frustration
A system is geometrically frustrated when its members cannot find a configuration that simultaneously minimizes all their interaction energies, as is the case for a two-dimensional antiferromagnet on a triangular lattice. A nonreciprocal system is one whose members have conflicting, asymmetric goals, as exemplified by an ecosystem of predators and prey. New work by Ryo Hanai of Kyoto University, Japan, has identified a powerful mathematical analogy between those two types of dynamical systems [1]. Nonreciprocity alters collective behavior, yet its technological potential is largely untapped. The new link to geometrical frustration will open new prospects for applications.
To appreciate Hanai’s feat, consider how different geometric frustration and nonreciprocity appear at first. Frustration defies the approach that physics students are taught in their introductory classes, based on looking at the world through Hamiltonian dynamics. In this approach, energy is to be minimized and states of matter characterized by their degree of order. Some of the most notable accomplishments in statistical physics have entailed describing changes between states—that is, phase transitions. Glasses challenge that framework. These are systems whose interactions are so spatially frustrated that they cannot find an equilibrium spatial order. But they can find an order that’s “frozen” in time. Even at a nonzero temperature, everything is stuck—and not just in one state. Many different configurations coexist whose energies are nearly the same.
Nonreciprocity is a common feature of the real world, which lacks Hamiltonian regularity. Besides thermally jiggling in the vicinity of an equilibrium configuration, states also dynamically cycle. Energy flows in and out, and conservative dynamics breaks down. Even Newton’s third law may not hold: the force on one agent from another need not be identical to the reverse force. Such nonreciprocal interactions are the norm in biology, ecology, and neuroscience, and they allow systems to spontaneously settle into states that are not stationary in time. The dynamical behavior of these nonreciprocal systems earned the field the name active matter. Much of that behavior is determined by frustration involving the agents.
Hanai set out to explore the parallel between spatial frustration in Hamiltonian systems and nonreciprocal frustration in dynamical systems. This goal might seem difficult at first sight. The equation of motion in a nonreciprocal dynamical system is not derived by minimizing an energy. Glasses have many distinct minima of the energy, which are so deep that once a system at low temperature has found a minimum, it stays there forever. These energy minima are far apart in configuration space but lie very close in energy. In 1975, physicists David Sherrington and Scott Kirkpatrick developed their profoundly influential model of a glass made of frustrated spins [2]. In 1980 Nobel Laureate Giorgio Parisi showed that in this model a multitude of energy states are degenerate [3]. Usually, degeneracy arises from a symmetry, but not in this case.
A dynamical system might settle down to a time-stationary fixed point in phase space where all the relevant variables become constant. Or it might become chaotic, meaning that some variables are wildly fluctuating, while others are tightly constrained. How does one characterize these time-dependent states? Because the equation of motion of their trajectories does not come from a Hamiltonian, there is no energy to be minimized to attain energetic stability. A better approach entails examining the stability of the trajectories themselves.
Aleksandr Lyapunov addressed that question in his doctoral thesis of 1892, which continues to provide tools for dynamical studies. Imagine perturbing a system infinitesimally. Does its orbit in phase space return to the initial trajectory or does it run away? Perturbations decay or grow as e𝜆t, where the growth rates 𝜆 are known as Lyapunov exponents. If all of them are negative, the system is stable and occupies a fixed point. If one of them is positive, then the orbit is unstable, and often this will presage chaos. If at least one is zero and the rest are negative, the system traces a limit cycle where the system oscillates in time—a time crystal (see Viewpoint: How to Create a Time Crystal). A Lyapunov exponent of zero tells you that you can reset the origin of that trajectory in time with no change in the physics. The negative values of the other Lyapunov exponents imply that there are directions in phase space that are on the margins of stability. And because the limit cycle orbits can be complicated, the marginal directions are not necessarily determined by symmetry.
Hanai’s starting point is a well-known model of coupled oscillators developed by physicist Yoshiki Kuramoto in the 1970s. This model consists of an array of overdamped, coupled circular pendula where the force between each of them depends in part on a coupling constant Jij between oscillator i and j. If Jij are all of the same sign, the oscillators will synchronize, and all the Lyapunov exponents will be negative but for one that is zero. When it comes to nonreciprocity, the extreme limit is perfectly antireciprocal: Jij = −Jji. Hanai derives a remarkable result: in such a case, all the Lyapunov exponents are zero. The system is fine tuned only in the sense of the antireciprocity: whereas Jij = −Jji, every Jij can be different. That result means that for N oscillators there are still N2/2 independent parameters. Despite there being no global symmetries, there is a huge manifold of marginal states.
What happens if internal symmetries are weakly broken? Hanai’s second major achievement is to identify what happens if small fluctuations, such as noise or heat, are added. He shows that, paradoxically, small fluctuations can lead to order. This finding is analogous to one in statistical physics. In 1980 a team led by physicist Jacques Villain pointed out that temperature reveals broken-symmetry states that are not visible at absolute zero, a phenomenon they dubbed "order as an effect of disorder" [4]. In their original example, a two-dimensional lattice model exhibited disordered paramagnetism at T = 0 yet long-range ferromagnetic order at nonzero temperatures.
Hanai’s work offers a set of new directions to pursue in frustrated dynamical systems of active agents. Neural networks are one potential arena. In 1982 spin glasses inspired John Hopfield to propose a Hamiltonian model of a neural network [5], which has since become a thread woven into modern machine-learning models. Two years ago, Kamesh Krishnamurthy and his collaborators studied gated neural networks as a large-scale statistical dynamical system [6]. They showed that one of the remarkable features of such models is that they all have many near-zero Lyapunov exponents. This feature is a useful idea for machine learning, because it means that images identifying, say, a dog are smoothly connected between breeds of dogs.
Ideas of marginal stability have a long history in physics, from glasses to sandpiles. Now, thanks to the work of Hanai and others, they may start to play out in neural networks and other dynamical systems.
References
- R. Hanai, “Nonreciprocal frustration: Time crystalline order-by-disorder phenomenon and a spin-glass-like state,” Phys. Rev. X 14, 011029 (2024).
- D. Sherrington and S. Kirkpatrick, “Solvable model of a spin-glass,” Phys. Rev. Lett. 35, 1792 (1975).
- G. Parisi, “Infinite number of order parameters for spin-glasses,” Phys. Rev. Lett. 43, 1754 (1979).
- J. Villain et al., “Order as an effect of disorder,” J. Phys. France 41, 1263 (1980).
- J. J. Hopfield, “Neural networks and physical systems with emergent collective computational abilities.,” Proc. Natl. Acad. Sci. U.S.A. 79, 2554 (1982).
- K. Krishnamurthy et al., “Theory of gating in recurrent neural networks,” Phys. Rev. X 12, 011011 (2022).