Precise Measurement of Hydrogen’s Energy Levels
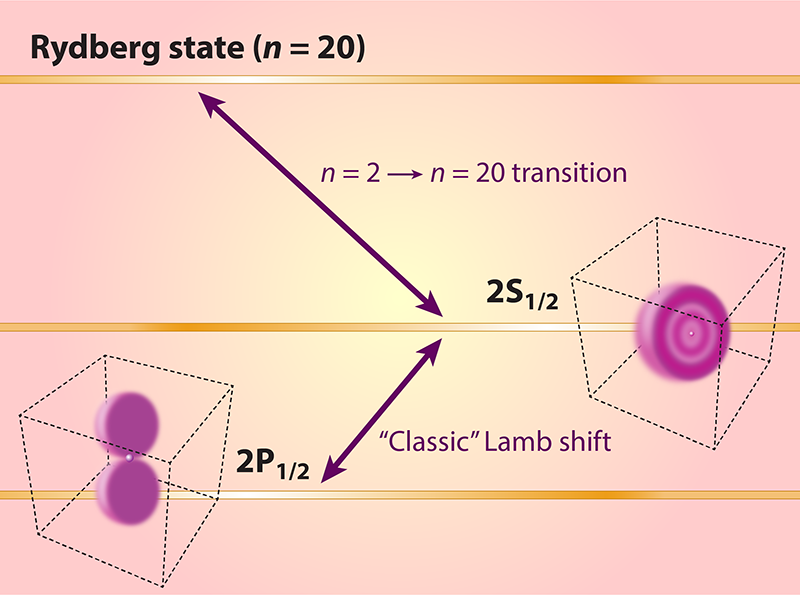
Physicists used to think they had a good idea of the size of the proton. Values derived from measurements of hydrogen’s emission spectrum and from electron-scattering experiments agreed with a proton radius of around 0.88 femtometers (fm). Then, in 2010, confidence was shaken by a spectral measurement that indicated a proton radius of approximately 0.84 fm [1]. In the years since, this “proton radius puzzle” has become even more of a head-scratcher, with some experiments supporting the original estimate and others finding an even greater discrepancy. Simon Scheidegger and Frédéric Merkt at the Swiss Federal Institute of Technology (ETH), Zurich, have now made precise new measurements of the transition energies between one of hydrogen’s metastable low-energy states and several of its highly excited states [2] (Fig. 1). These measurements allow the researchers to derive some of the atom’s properties, such as its ionization energy, with greater confidence, which should help clear up some of the confusion.
The 2010 study that “shrank the proton” (as the title of the editorial summary in Nature jokingly stated) concerned the 2S–2P1/2 Lamb shift [1]. According to Dirac’s predictions, the 2S and 2P1/2 levels of atomic hydrogen should be degenerate. The Lamb shift refers to the lifting of this degeneracy by quantum electrodynamic (QED) effects, the largest contribution being the electron “self-energy” due to interactions with virtual photons. Once this and other QED effects are accounted for, a tiny shift of the bound-state energy levels remains, which can be attributed to the proton’s finite size. By measuring this residual energy shift, one can determine the proton radius directly. The authors of the 2010 study did so using hydrogen atoms in which the electron was replaced by its heavier cousin, the muon, since the finite-size effect is stronger in this system.
Ever since that surprise result, researchers have tried to pin down the proton radius both directly, via the finite-size effect, and indirectly, via the Rydberg constant. The Rydberg constant relates an atom’s energy levels to other physical constants and is one of the key inputs used in calculations of the proton radius. Determining its value requires painstaking measurements of the transition energies between hydrogen’s various states. Several groups have made monumental efforts in this regard, but the values they derive for the proton radius have been all over the place. A 2018 measurement of the 1S–3S transition by a group in France gave a value of about 0.88 fm [3], a 2019 measurement of the classic Lamb shift (this time in regular hydrogen) by a group in Canada came up with a value of about 0.833 fm [4], and a 2017 measurement of the 2S–4P transition by a group in Germany suggested a similarly low value of about 0.834 fm [5]. In 2020, the group in Germany arrived at a slightly higher value of 0.848 fm [6]. In 2022, finally, from measurements of the 2S–8D transition, a group at Colorado State University proposed a “compromise value” of about 0.86 fm [7].
Scheidegger and Merkt, like some of their predecessors, start from hydrogen’s metastable 2S level. This state has a natural lifetime of 0.122 seconds and provides a convenient “launchpad” for transitions to high principal quantum numbers. But the researchers go higher than most, accomplishing measurements of transitions from that 2S launchpad into the realm of highly excited “Rydberg” states with principal quantum numbers n of 20–24. These Rydberg states have undefined angular momenta but, due to the application of an external electric field, defined Stark-state parabolic quantum numbers. This field lets the researchers control and distinguish between different fine-structure-resolved and hyperfine-structure-resolved hydrogen eigenstates that would otherwise overlap in energy. Scheidegger and Merkt find that all of the measured transitions can be fitted by a unified theoretical model that takes the quantum numbers of the Rydberg states into account. In fact, they use the observed splitting to calibrate the electric field. This in itself is no small achievement, as it requires the diagonalization of complicated hyperfine-resolved matrices of the Stark operator.
In order to understand the rationale of their experiment, one needs to know that, to a good approximation, S states, and only S states, have a nonvanishing probability density at the nucleus. Together with their spherical symmetry, this makes these states sensitive to the proton radius, with the nuclear-size correction—that is, the energy-level adjustment needed to account for the proton’s finite size—proportional to 1/n3. In fact, it is the sensitivity of the 2S state to the proton radius and the insensitivity of the 2P states, which makes it possible to determine the proton radius using the 2S–2P1/2 Lamb shift alone.
But wait. Scheidegger and Merkt’s goal is to determine a precise, accurate value of the Rydberg constant from measurements of transition energies. If the energy levels of S states—including their 2S launchpad—depend on the nuclear size, how can they obtain a value that’s independent of the proton radius?
The answer lies in the additional input that they use—namely, the value of the Lamb shift transition 2S–2P1/2 measured by the group in Canada in 2019 [4]. By adding that value to the frequency of the transition from the 2S state to a highly excited Rydberg state, Scheidegger and Merkt effectively measure the transition from the 2P1/2 state to the highly excited Rydberg state. Now, both the upper and lower levels are largely independent of the proton radius. One can always find such combinations of frequencies that are independent of the proton radius and therefore give the Rydberg constant. Here, the lucky circumstance is that the prefactors that correct for the proton radius are unity. For example, if one wanted to determine the Rydberg constant on the basis of the 1S–2S and 2S–4P transition frequencies, the prefactors would be 1/7 and −1. In Scheidegger and Merkt’s work, by contrast, the simple sum of the 2S–2P1/2 and the 2S-to-n = 20 frequencies eliminates the proton radius.
Scheidegger and Merkt’s determination of the Rydberg constant comes with a caveat: other measurements of the classic Lamb shift transition 2S–2P1/2 exist—notably, by Lundeen and Pipkin [8] and Hagley and Pipkin [9]. Those measurements, although carried out in the 1980s and 1990s, are not much less precise than the 2019 measurement by the group in Canada [4] but indicate a larger proton radius. The reliability of Scheidegger and Merkt’s determination depends on which group’s measurement of the 2S–2P1/2 Lamb shift is most accurate. In order to put this dependence into perspective, note that classic Lamb shift measurements need to overcome an important obstacle—the extremely short lifetime of the hydrogen 2P state. This state is one of the shortest-lived excited states in all neutral atoms, and measuring its transitions presents a major challenge. Thus, we can conclude that there remains work to be done before we can be confident about the true value of the Rydberg constant.
This caveat does not apply to Scheidegger and Merkt’s measurement of the value of the ionization energy of atomic hydrogen. The ionization energy can be determined very reliably, because the only additional input data needed are the hydrogen 1S–2S frequency and the 1S hyperfine frequency. These frequencies are both known to have more than sufficient accuracy, as measurements are facilitated by the very small natural linewidths of both the 1S–2S frequency and of the 1S hyperfine transition [6–10]. As a result, the value for the ionization energy of hydrogen obtained by Scheidegger and Merkt constitutes not only the most precisely known ionization energy yet known of any bound system but also one of the most precisely known of all physical constants.
References
- R. Pohl et al., “The size of the proton,” Nature 466, 213 (2010).
- S. Scheidegger and F. Merkt, “Precision-spectroscopic determination of the binding energy of a two-body quantum system: The hydrogen atom and the proton-size puzzle,” Phys. Rev. Lett. 132, 113001 (2024).
- H. Fleurbaey et al., “New measurement of the 1S–3S transition frequency of hydrogen: Contribution to the proton charge radius puzzle,” Phys. Rev. Lett. 120, 183001 (2018).
- N. Bezginov et al., “A measurement of the atomic hydrogen Lamb shift and the proton charge radius,” Science 365, 1007 (2019).
- A. Beyer et al., “The Rydberg constant and proton size from atomic hydrogen,” Science 358, 79 (2017).
- A. Grinin et al., “Two-photon frequency comb spectroscopy of atomic hydrogen,” Science 370, 1061 (2020).
- A. D. Brandt et al., “Measurement of the 2S1/2–8D5/2 transition in hydrogen,” Phys. Rev. Lett. 128, 023001 (2022).
- S. R. Lundeen and F. M. Pipkin, “Measurement of the Lamb shift in hydrogen, n = 2,” Phys. Rev. Lett. 46, 232 (1981).
- E. W. Hagley and F. M. Pipkin, “Separated oscillatory field measurement of hydrogen 2S1/2–2P3/2 fine structure interval,” Phys. Rev. Lett. 72, 1172 (1994).
- Th. Udem et al., “Phase-coherent measurement of the hydrogen 1S–2S transition frequency with an optical frequency interval divider chain,” Phys. Rev. Lett. 79, 2646 (1997).