Network Science Applied to Urban Transportation
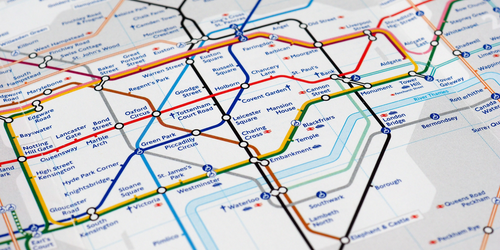
Urban railway and subway systems have intricate structures that often include loops and branches. Over the past few decades, scientists have used a variety of methods to model these transportation networks, with the models ranging in both complexity and accuracy. Now researchers in Italy have developed a simple model based on network theory to reproduce the labyrinthine structures found in, for example, the UK’s London Underground subway system [1]. The researchers say that their model could enable more-optimized urban planning.
The team’s model generates a transportation network by mapping an urban area’s spatial features, such as the distribution of people and amenities it contains, to a lattice of interconnected nodes. The connection between a pair of nodes has a so-called weight, which represents how quickly that connection can be traversed in the simulated network. These weights are adjusted until the time needed to travel between two nodes is minimized for all pairs of nodes. A key novelty of the model is that this optimization process accounts for realistic human-travel behaviors and traffic-congestion effects.
To demonstrate their model, the researchers used data on the density of people and amenities in Greater London and generated an optimized subway system for the region. They found that the system they generated had remarkably similar features to the region’s actual subway system, the London Underground. The researchers suggest that their model could be extended to help urban planners improve existing transportation networks and even design new ones.
–Ryan Wilkinson
Ryan Wilkinson is a Corresponding Editor for Physics Magazine based in Durham, UK.
References
- S. Bontorin et al., “Emergence of complex network topologies from flow-weighted optimization of network efficiency,” Phys. Rev. X 14, 021050 (2024).