Keeping up with the noise

Ralf Metzler

Viewpoint

Keeping up with the noise

Physics Department, Technical University of Munich, 85747 Garching, Germany

May 4, 2009• Physics 2, 36

Faster does not mean more precise—a new view of how proteins diffuse and bind to a specific site on the DNA reassesses the role noise plays in the biochemical production line that creates biomolecules from genes.

Figure caption — **Figure 1:** Facilitated diffusion mechanisms in the Berg-von Hippel model. Transcription factors searching for their specific binding site on a DNA chain combine interdomain exchange (decorrelating 3D volume diffusion), intradomain exchange (microhops, short 3D excursions), sliding (1D diffusion along the DNA), and intersegment transfers where the DNA loops back to itself. Inset: Once the transcription factor docks onto its specific binding site it will attract RNA polymerase that produces an RNA copy of the corresponding gene.

Diffusional and biochemical noise occur naturally in the fundamental processes of gene regulation, yet we know that genetic systems may be extremely stable. Facilitated diffusion—the interplay of three-dimensional and one-dimensional search of DNA binding proteins for their specific binding sites—has been proposed to explain the regulation speed and lowering of noise effects. Now, a modified view of the causes and consequences of diffusional noise is presented by Gašper Tkačik and William Bialek (Princeton University and The Rockefeller University) in a paper in Physical Review E [1], concluding that diffusional noise is not significantly reduced by the mechanisms of facilitated diffusion.

Biological physics is often referred to as $k_{B} T$ -physics because typical free energies for the molecular processes are of the order of a few times the Boltzmann energy $k_{B} T$ . Due to thermal activation, stochasticity naturally emerges as a player in many cellular processes. This is particularly true for gene regulation (that is, the processes that control how cells turn genetic information into proteins on demand). What are the numbers? In bacteria the single DNA molecule is a few millimeters long, corresponding to a few million base pairs (bp—the molecular building blocks of the paired molecules adenine-thymine and guanine-cytosine that make up the familiar double helix). The information encoded on the DNA by the specific sequence of base pairs is divided into genes, each amounting to some 1000 base pairs on average. Each gene stores the biochemical blueprint for a gene product: an RNA or a protein. During cell development, or to respond to external signals, a cell reads out genes and produces proteins on demand, and at different levels. During this process, a molecular motor called RNA polymerase produces a single-stranded copy of the base pairs making up the gene (transcription). In a second step this RNA transcript is converted into proteins in biochemical factories called ribosomes. The overall number of proteins even in a bacteria cell is of the order of $3 x 10^{6}$ , yet some proteins occur at very small concentrations, down to few dozen copies per cell.

How can the reading out of the information of a given gene be controlled? Reacting to some signal, a given sequence-specific DNA binding protein [a so-called transcription factor (TF)] will bind to its specific binding site on the DNA (some 15–20 bp long). The TF will promote (the TF is an activator) or block (the TF is a repressor) the reading out of the associated gene. A decade-old question is how a TF finds its designated binding site, and so efficiently. Using active modes of transportation to bring a TF to its specific binding site at the expense of biochemical energy would be far too costly for the cell. A TF in fact simply diffuses to its specific binding site. Naively one might assume that the TF diffuses in three dimensions until hitting its target site. According to the classical Smoluchowski picture of diffusion-limited reaction rates this would occur with a rate $k = 4 π D b$ , where $D$ is the three-dimensional diffusion constant and $b$ the size of the target. With $D \approx 10 μ m^{2} / s$ and $b \approx 1 nm$ , one would obtain $k = 10^{8} [(mol/l)s]$ . For the Lac repressor, a typical transcription factor, the measured binding rate is 100 times larger.

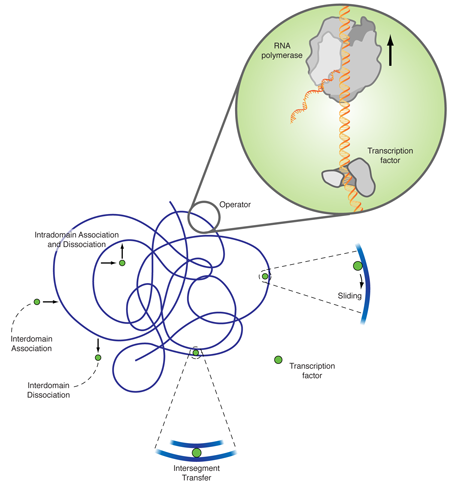
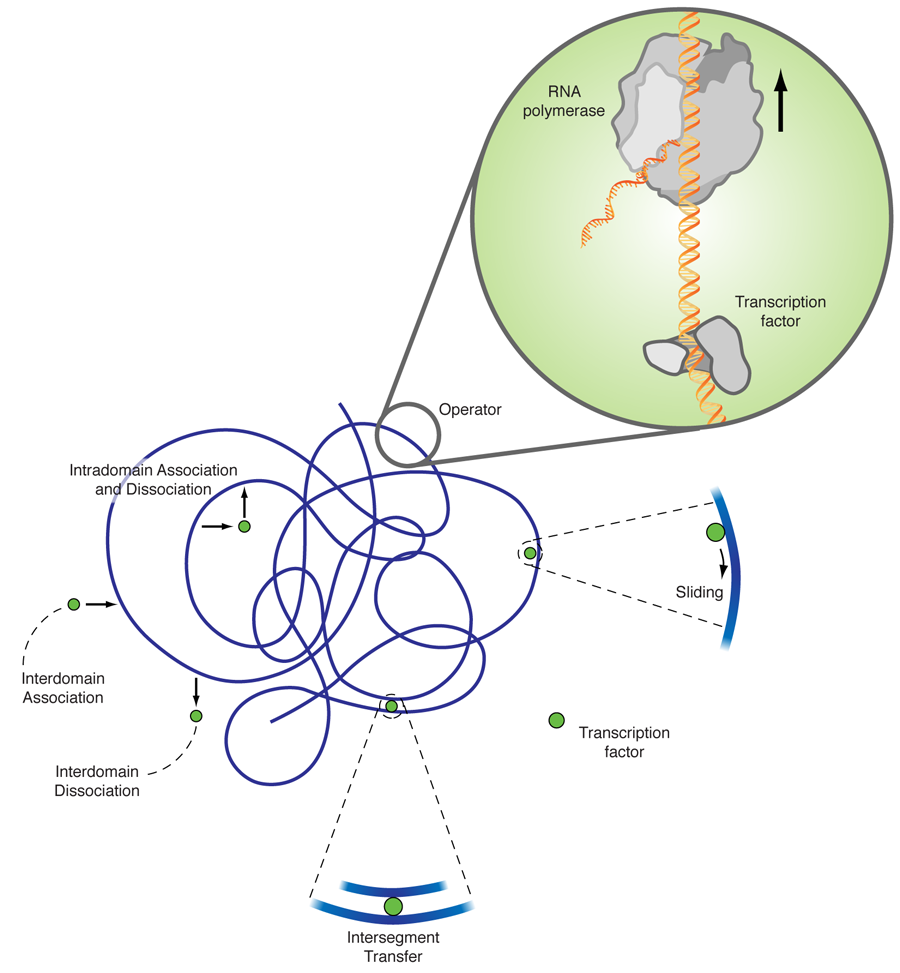
The explanation of this discrepancy lies in additional diffusion mechanisms, as originally proposed by Adam and Delbrück [2], and Richter and Eigen [3]. The facilitated diffusion model [4] combines three-dimensional diffusion and diffusion along the DNA chain. While three-dimensional diffusion is efficient in (partially) decorrelating the unbinding from the rebinding sites, it is fairly inefficient in locating a small target in three-dimensional space. One-dimensional diffusion eventually hits every point on a finite line due to its compact trajectory; however, many revisitations to already searched sites make it very inefficient. The combination of intermittent one- and three-dimensional diffusion gives rise to a search strategy that is much more efficient than each of its contributing individual mechanisms. As sketched in Fig. 1, apart from one- and three-dimensional diffusion a transcription factor can also jump between two DNA segments, which by DNA looping, are close by in the embedding space but far apart in the chemical distance measured along the DNA. In a recent single DNA setup it was shown that intersegmental jumps can further speed up the search [5].

If, during a one-dimensional diffusion event, the target is within the typical distance travelled before unbinding back to the bulk, the target will very likely be found. This is why the facilitated diffusion mechanism introduces an effective so-called “antenna” length, replacing the target size in the above classical 3D diffusion result. As a consequence the target search time gets significantly reduced. This is good news. Focusing solely on the search rate, however, would be like minimizing the journey time of a train or flight itinerary and neglecting slight delays due to which the connecting train or flight will be missed. In order to judge the likelihood of missing one’s connection one needs to know the distribution around the mean journey time. This is true for any first passage process: the mean first passage time provides only very limited information, it is a more or less noisy quantity.

So what about that noise in gene regulation? Transcription factors, being subject to stochasticity, do not arrive at their designated binding site on a fixed train schedule. On average, they arrive with a search rate determined by all the system parameters. An individual transcription factor’s arrival time then lies within a distribution around that mean value. And so does the initiation moment for the regulation of a specific gene after some stimulus. This is where the analysis of Tkačik and Bialek [1] (following two earlier works [6]) kicks in.

Noise, or stochasticity, in gene expression has been recognized as inevitable in a number of works [7]. For instance, a clonal population of E. coli cells showed considerable variations in their phenotype (i.e., the set of observable traits attributable to a genotype). The work by Tkačik and Bialek goes one step further. It explicitly addresses the fundamentals of diffusional noise, as quantified by spatial concentration fluctuations. A priori, one would expect that the target size enhancement due to the facilitated diffusion mechanism would reduce the noise. Namely, the antenna harvests incoming binding proteins in a larger range and therefore levels out the fluctuations. Remarkably, the authors find that this is not the case. In contrast, while enhancing the search speed, facilitated diffusion does not significantly reduce diffusional noise, for realistic parameters. Intuitively, the counterargument against the “obvious” noise reduction due to a larger antenna size is that this antenna harvests proteins that bind to a cylindrical structure of length of some 100 base pairs ( $\approx 35 nm$ ) and effective radius $\approx 3.5 nm$ [5]. This is apparently not the same as having an increased spherical target.

In a careful analysis the authors consider one- and three-dimensional diffusion mechanisms for a cylindrical DNA geometry. However, in their discussion they give convincing arguments that a fluctuating DNA density would not change the magnitude of the noise significantly, concluding that “all these results point to the basic physics of diffusion as setting a limit to precision of a fundamental biological process, transcriptional regulation,” and that this limit “is not easily evaded by the…complexities of protein motion along a DNA molecule.” In that sense the paper by Tkačik and Bialek sets a new approach to gene regulation, building the analysis of diffusional noise on a fully physical foundation. It shows that noise is an unavoidable ingredient. As recent studies show, noise is not bad per se—in many cases it offers the biological system a chance to differentiate, among other things. At the same time cells manage to keep some genetic units surprisingly stable. The famed example is the so-called $λ$ switch, a genetic decision unit controlled by two different antagonist TFs in an E. coli bacterium infected by a virus. This switch decides whether the virus remains dormant or breaks out and kills the host cell, but owing to noise the $λ$ switch fails in one out of $10^{8}$ cell generations. In view of the current results it will be interesting to understand more precisely how the cell manages to control the noise with such bravura.

Of course, all this is just the beginning. There are still many details, some very important, we have to learn about and take into consideration when approaching the actual living organism. There is the compaction of the DNA, the inner structure of a biological cell, the high molecular crowding of biopolymers in the cytoplasm (the inner medium of the cell) and the consequences to diffusion and performance of enzymes and motor proteins, the competition for DNA binding between thousands of proteins, and more. In addition there is a structure in the genetic code, for instance, in which interacting genes turn out to be co-localized either within the genomic sequence or in the embedding space. On the basis of the approach by Tkačik and Bialek it will be interesting to see which of these phenomena may lead to significant additional features in the dynamics of gene regulation. For instance, the claim that due to molecular crowding even smaller biopolymers like transcription factors no longer diffuse normally according to $〈 r^{2} (t) 〉 ≃ D t$ in the cytoplasm, but transiently subdiffuse $〈 r^{2} (t) 〉 ≃ D_{α} t^{α}$ , with $0 < α < 1$ (see Ref. [8]), would pose interesting consequences for the influence of the noise.

Ultimately, the understanding of how a cell controls the noise may turn out to be one of the keys to understand its evolutionary advantage, for instance, in cells that are more compact or better designed. Gene regulation in living cells, even bacteria, is a complex process involving various length scales. Both spatial correlations and noise are being increasingly appreciated as important ingredients in the molecular control of cellular processes. Physicists can help to develop better models appreciating the different facets of gene regulation, and this new work by Tkačik and Bialek will help pave the way to such a new view.

References

G. Tkačik and W. Bialek, Phys. Rev. E 79, 051901 (2009)
G. Adam and M. Delbrück, in Structural Chemistry and Molecular Biology, edited by A. Rich and N. Davidson (W. H. Freeman, San Francisco, CA, 1968)[Amazon][WorldCat]
P. H. Richter and M. Eigen, Biophys. Chem. 2, 255 (1974)
O. G. Berg, R. B. Winter, and P. H. von Hippel, Biochemistry 20, 6929 (1981); R. B. Winter, O. G. Berg, and P. H. von Hippel, ibid. 20, 6961 (1981)
B. v. d. Broek, M. A. Lomholt, S.-M. J. Kalisch, R. Metzler, and G. J. L. Wuite, Proc. Natl. Acad. Sci. USA 105, 15738 (2008)
W. Bialek and S. Setayeshgar, Phys. Rev. Lett. 100, 258101 (2008); Proc. Natl. Acad. Sci. U.S.A. 102, 10040 (2005)
We quote two representative works: M. B. Elowitz et al., Science 297, 1183 (2002); E. Ozbudak et al., Nat. Genet. 31, 69 (2002)
R. Metzler and J. Klafter, Phys. Rep. 339, 1 (2000)

About the Author

Ralf Metzler received his doctorate in physics from the University of Ulm, Germany, in 1996. After postdoctorates at Tel Aviv University and MIT, he was appointed assistant professor at the Nordic Institute for Theoretical Physics (NORDITA), which was then in Copenhagen. After a period as Canada Research Chair in Biological Physics at the University of Ottawa, he moved to the Technical University of Munich as a professor. Since 2011, he has been chair professor for theoretical physics at the University of Potsdam and is an Alexander von Humboldt Polish Honorary Research Fellow. His research focuses on nonequilibrium statistical physics and (anomalous) stochastic processes, with applications to biological and soft matter systems. In 2009 he was recognized as an Outstanding Referee by the American Physical Society.