Fractional charges fly between planes

Fiona J. Burnell; Shivaji L. Sondhi

Viewpoint

Fractional charges fly between planes

Department of Physics, Princeton University, Princeton, NJ 08544, USA

June 15, 2009• Physics 2, 49

The fractional quantum Hall effect, thought to be special to two dimensions, may also flourish in three, providing a possible explanation for anomalies observed in certain 3D materials in high magnetic fields.

Figure caption — **Figure 1:** In each layer of electron gas, electrons are visualized as composed of partons, each with a third of the electronic charge $e$ . The partons live in cyclotron orbits, whose number is a third of the cyclotron orbits of the electrons themselves. Under certain conditions partons can hop between layers, introducing an element of three dimensionality to a previously two-dimensional world.

One of the central themes of condensed matter physics is the richness of phases of matter and the transitions between them. One current intellectual frontier is the study of topological or fractionalized phases of matter where the low energy and long distance description involves excitations with quantum numbers different from those of the constituent particles [1]. The most spectacular examples of this class are the large and growing set of fractional quantum Hall phases seen in two-dimensional electron gases. Motivated by recent experiments on the three-dimensional materials bismuth and graphite [2,3], Michael Levin and Matthew Fisher at the University of California, Santa Barbara, writing in Physical Review B [4], suggest that fractional Hall states can be much more three dimensional than our current understanding of these phases allows; specifically, they propose phases in which fractionally charged quasiparticles can move in three dimensions. Their approach opens the possibility of constructing a completely new class of three-dimensional states for electrons in strong magnetic fields.

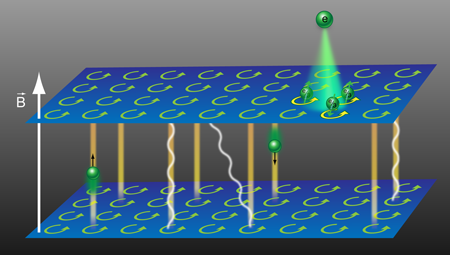
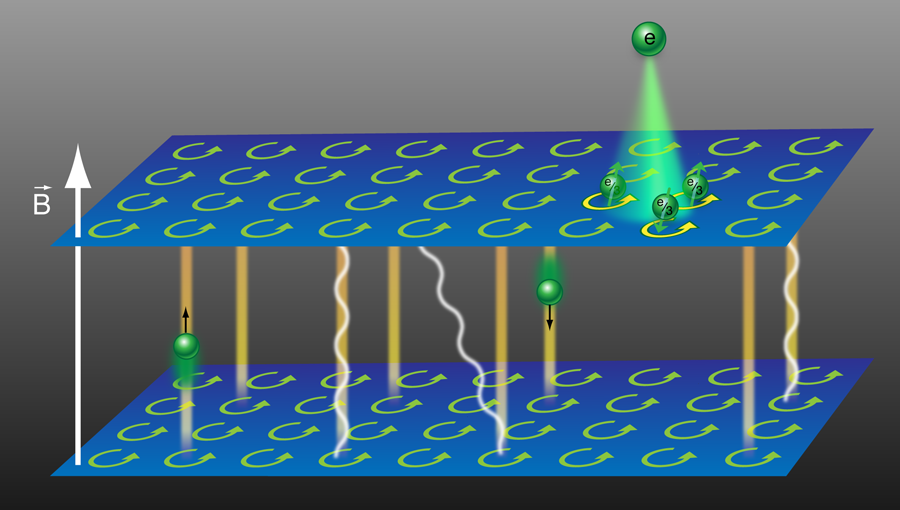
The problem at issue (see Fig. 1) is to consider a set of electrons that live on a stack of $N$ two-dimensional layers placed in a strong perpendicular magnetic field where we will produce three dimensionality by taking the limit $N \to \infty$ . For $N = 1$ we have the magic of the quantum Hall effect—at selected rational filling factors $ν$ , the electrons arrange themselves into an especially favorable topologically ordered “quantum Hall liquid” state. The filling factor is the ratio of the number of particles to the number of flux quanta threading the system. These quantum Hall liquids then produce the remarkable steplike quantization of the Hall resistance near the selected rational values of $ν$ . The fundamental challenge of generalizing this to $N > 1$ is that our understanding of the single-layer physics rests on constructing many-particle wave functions, which introduce a complex pattern of correlations between electrons in the plane. When electrons move freely between two-dimensional planes these correlations, along with their intriguing topological properties, are destroyed.

One solution to this problem has been to suppress motion between the layers so that each electron moves in a definite layer. This still allows electrons to correlate with their neighbors in nearby planes, giving rise to new quantum Hall states [5,6] of which some have been observed in experiments on double-layer systems [7]. A second solution, which works for a small number of layers, is to work in the limit where the kinetic energy for motion between layers dominates. In this limit, say for a bilayer, one can simply freeze the interlayer motion into a uniform superposition over the layers and thus return to an effectively two-dimensional problem and quantum Hall state. The reader will note though that this cannot work as $N \to \infty$ and the eigenvalues of the interlayer kinetic energy become continuous. Away from these two limits, it has remained a challenge to find states that still give rise to quantized Hall behavior. Levin and Fisher set out to address this challenge.

The inspiration for their approach (and earlier work of Jain [8]) is drawn from a superficially unrelated area of physics—magnetism near the onset of high-temperature superconductivity. The fundamental conundrum, however, is the same: how can strong interactions and itinerancy be accommodated simultaneously? One approach popularized in this setting, and inspired by Anderson’s “RVB” ideas on fractionalization in doped Mott insulators [9], is to assume that quantum numbers will fractionalize, and subdivide the electron into a product of partons, each of which carries some fraction of an electron’s quantum numbers. The rationale here is that if fractionalization emerges as the end product of the interactions, then the parton description already captures the most dramatic effect of the correlations, and a noninteracting wave function of partons gives a reasonable starting point from which to explore this physics. The remaining challenge is to understand when partons can describe new states of matter. The situation is subtle: chopping the electron into multiple partons introduces new degrees of freedom called gauge fields. In conventional phases, these gauge fields confine the partons, binding them together so that only the composite electrons play a role in the physics. If this confinement can be avoided, partons can be a powerful tool for describing the complex behavior of strongly correlated particles.

By applying an analogous approach to the fractional quantum Hall effect, Levin and Fisher construct states that both reflect the intralayer correlations responsible for these states’ interesting topological properties, and allow particles to propagate in all three directions of space. Working from the two-dimensional fractional quantum Hall state at $1 / 3$ filling per layer, they subdivide the electron into three partons, each with electric charge $e / 3$ . By analogy with the noninteracting parton states mentioned above, they construct approximate wave functions for the system. When partons are confined to their layers, the state describes multiple noninteracting copies of the two-dimensional $1 / 3$ -filled quantum Hall state. If this confinement does not materialize, the resulting states are different from both the correlation-dominated and tunneling-dominated states described above. For finite $N$ , this analysis leads to three flavors of charge $e / 3$ quasiparticles with variant fractional statistics. Still, these states bear a family resemblance to the previously known quantum Hall states.

More germane to recent experiments in layered crystals [2,3], however, is the question of what happens in systems with an infinite number of layers. Here the parton state is qualitatively different from any known state that incorporates strong correlations within the layers. Its first striking feature is the true three dimensionality of the liberated partons, which are free to move between layers. Consistent with this, the partons become fermionic—fractional statistics being possible only in the strictly two-dimensional setting. The second striking feature is the presence of a bulk, three-dimensional mode, which is a “photon” associated with the gauge fields discussed above. Finally, there is the prediction of a distinct surface interlayer conduction mechanism associated with this state.

As with any fundamentally new approach, the work of Levin and Fisher poses as many questions as it answers. First, there is currently no transparent transformation that maps the microscopic action for electrons directly onto an action for partons in these quantum Hall systems. In magnetism, establishing such a connection gives us a framework for asking when parton states are likely to be energetically stable. This provides valuable insight about which physical systems are most likely to exhibit the consequent new phases. Second, their formalism does not actually lead to electronic wave functions that can describe the new phases. This is an anomaly in that our understanding of quantum Hall physics is largely based on constructing and studying such wave functions. A third interesting question is whether numerical studies can find evidence of the parton states that Levin and Fisher propose at intermediate values of interlayer kinetic energy. Finally, multilayer structures are known to be energetically prone to spontaneous charge transfer between layers [10] and this will complicate life for the Levin-Fisher states.

Wedding the parton construction first used to address puzzles in high-temperature superconductivity with topological phases in the fractional quantum Hall effect opens a new avenue from which to approach the challenging problem of three-dimensional electrons in a strong magnetic field. This is an intermediate coupling problem; Levin and Fisher provide creative approximations to analyze it. The field is now open for further applications of these ideas with generalizations of two-dimensional non-Abelian states presenting an especially inviting target.

References

X.-G. Wen, Ann. Phys. New York 316, 1 (2005)
K. Behnia, L. Balicas, and Y. Kopelevich, Science 317, 1729 (2007)
Y. Kopelevich, B. Raquet, M. Goiran, W. Escoffier, R. R. da Silva, J. C. Medina Pantoja, I. A. Lukyanchuk, A. Sinchenko, and P. Monceau, arXiv:0903.2369 (2009)
M. Levin and M. P. Fisher, Phys. Rev. B 79, 235315 (2009)
B. I. Halperin, Helv. Phys. Acta 56, 75 (1983)
J. D. Naud, L. P. Pryadko, and S. L. Sondhi, Nucl. Phys. B 594, 713 (2001); arXiv:cond-mat/0006506 and references therein
M. Shayegan, in Theory and Experiments II, High Magnetic Fields Science and Technology, Vol. 3, edited by F. Herlach and N. Miura (World Scientific, New Jersey, 2003)[Amazon][WorldCat]
J. K. Jain, Phys. Rev. B 40, 8079 (1989)
P. A. Lee, N. Nagaosa, and X.-G. Wen, Rev. Mod. Phys. 78, 17 (2006)
F. J. Burnell, B. A. Bernevig, and D. P. Arovas, Phys. Rev. B 79, 155310 (2009)

About the Authors

Fiona Burnell will finish her Ph.D. at Princeton University, NJ, in the summer of 2009, and will hold a post-doctoral research fellowship at All Soul’s College, Oxford, beginning in the fall of this year. She is currently a graduate fellow at the Kavli Institute for Theoretical Physics in Santa Barbara, CA. Her research interests include frustrated quantum magnetism and spin liquids, topological phases, and the quantum Hall effect.

Shivaji Sondhi is a Professor of Physics at Princeton University. He is a condensed matter theorist whose research has been primarily in the subset of the field concerned with quantum many-body physics. His current interests lie in the theory of topological phases, frustrated magnetism, and the statistical mechanics of quantum computation.