Entangled in a dating game

Mark M. Wilde

Viewpoint

Entangled in a dating game

School of Computer Science, McGill University, Montreal, Quebec H3A 2A7, Canada

March 14, 2011• Physics 4, 21

Entanglement, a crucial resource in quantum information theory, can also improve communication over a classical channel.

Figure caption — **Figure 1:** The game board for “Guess That Button.” The game show host gives Alice the game board, and Alice pushes one of the four buttons. Observe that there are exactly three edges (green, blue, or red) touching the button that Alice pushes. The game show host then gives the game board to Bob, and one of these three edges randomly lights up. It is Bob’s task to guess which button Alice pushes. A classical strategy has a maximum success probability of $5 / 6$ , but entanglement can increase this to about $90 %$ .

In the $90$ s, when quantum information was a young field, Charles Bennett and others found that entanglement—a property of quantum mechanics that links different quantum objects so that they cannot, in effect, behave independently—can assist in teleporting quantum bits [1] and in increasing communication rates over both noiseless [2] and noisy quantum channels [3]. However, they also suggested that entanglement would not be particularly helpful [3] when it came to enhancing the capacity of a classical channel. Given this, it is perhaps surprising that Robert Prevedel and his coauthors at the University of Waterloo, Canada, in their paper in Physical Review Letters, show that entanglement can be helpful in a noisy classical channel [4]. They observe this effect because their setup differs from that considered by Bennett and others. Rather than allowing many uses of the classical channel and demanding that communication error rates become negligible in the limit of many uses (as is conventional in quantum information theory), they allow just one use of the classical channel and consider maximizing the chances for a receiver to guess a sender’s transmitted message. The upshot is that entanglement can improve performance here.

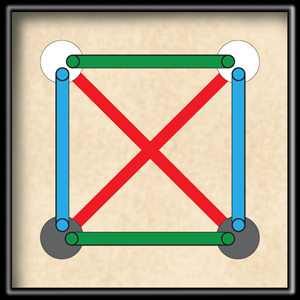
Perhaps the best way to explain how entanglement plays a role is with a dating game that we’ll call “Guess That Button.” The game has two contestants, Alice and Bob, who sit in different rooms. The game show host gives Alice the game board (see Fig. 1), and Alice randomly pushes one of the four buttons on the board. Three edges (green, blue, and red) touch the button that Alice pushes. The host then takes the board from Alice, goes to Bob’s room, hands him the board, and one of these three edges randomly lights up. It is then Bob’s goal to “guess that button.” If he does so correctly, he wins a free dinner with Alice at the nicest sushi restaurant in town.

Bob is a bit helpless without more information. Two buttons touch each edge, and he really has to guess randomly which button Alice pushed. His chances of winning are $50 / 50$ , not great odds for a dinner date. It turns out that Alice kind of likes Bob (and she really likes sushi). She realizes that his chances of winning are slim, so she asks the game show host if he’ll allow a strategy with higher chances for a win. The game show host agrees and suggests that Alice randomly pushes either a white or a grey button. He says now that it is Bob’s task to guess the color of the button that she pushes. Alice and Bob agree beforehand (a “code” in the parlance of communication theory) that she’ll randomly pick just one of the buttons on the left.

Bob’s chance to “guess that button” increase significantly with this modified strategy. Suppose Alice pushes the white button on the left. In this case, at random, either the blue, red, or green edge touching it lights up. If the green or red edge lights up, then $2 / 3$ of the time Bob knows Alice pushed the white button because they agreed she wouldn’t push a button on the right. If the blue edge lights up, then $1 / 3$ of the time Bob has to guess randomly which button Alice pushed. So the chances of Bob guessing correctly when Alice pushes the white button on the left are $2 / 3 + 1 / 3$ * $1 / 2 = 5 / 6$ . Since the game board is symmetric, the chances of winning are the same if Alice pushes the grey button. So, the overall chance for them to win a free sushi dinner is $5 / 6$ . It turns out that this is the best strategy they could use while still keeping the game interesting, that is, a game of chance.

Now enter entanglement. Suppose the host allows Alice and Bob to share two entangled particles before the game begins. Having access to good entanglement increases their chances of winning that dinner if they employ the following strategy: Alice first randomly decides whether she’ll push one of the two white buttons on the top or one of the two grey buttons on the bottom, and she measures her half of the entangled state in a particular way depending on this choice. Each measurement has two possible outcomes. After making this “top or bottom” choice and performing the measurement, she then pushes the button on the left or on the right, depending on the outcome of the measurement. The game show host gives the board to Bob, and one of the green, blue, or red edges touching the button that Alice pushed, randomly lights up. The green edge lights up $1 / 3$ of the time, and if it does, Bob can determine with certainty whether Alice pushed a white or grey button. If the red or blue edge lights up, Bob employs a different strategy. He measures his half of the shared entanglement in a particular way, depending on certain information that he would like to learn. With an $85 %$ chance, he can correctly determine either the red or blue edge that touches the button Alice pushed. This is due to the strong correlations in entanglement—classical correlations would only give him a $75 %$ chance of learning this information correctly. So, if the blue edge lights up, it is better for him to determine the red edge, and he chooses the measurement that will give him this information correctly $85 %$ of the time. It is better to determine red because he already knows the blue edge, and if he determines the red edge correctly, he can figure out exactly which button Alice pushed, and thus whether it was white or grey. Similarly, if the red edge lights up, he can correctly determine $85 %$ of the time that the blue edge touches the button Alice pushed, and then make a good guess at which button Alice pushed. Adding things up, he’ll guess correctly the color of the button Alice pushed $1 / 3$ of the time (the chance that the lit edge is green), and he’ll guess correctly $2 / 3$ * ( $85 %) = 57 %$ of the time when the lit edge is red or blue. Thus the total chance of guessing the color of the button Alice pushed is about $1 / 3 + 57 % \approx 90 %$ . If they only share classical correlations, the total chance is $1 / 3 + 2 / 3 * (75 %) = 5 / 6$ , which is no better than the classical strategy in the previous paragraph. Thus entanglement gives a significant $7 %$ boost to their chances of winning a sushi dinner.

To verify that these results aren’t just magic, Prevedel et al. performed an experimental implementation of the “Guess That Button” game on an optics bench in their quantum optics lab. In place of real contestants in a game show, they simulated the game using polarization entangled photons between two measurement devices, Alice and Bob, and an electronic logic circuit connected to a random number generator that implemented the noisy channel (or, in our analogy, selected randomly which edge would light up). The polarization entanglement was generated using a process called down-conversion, in which a high-energy photon can break into two lower energy photons. One of the photons in the pair was sent to Alice, the other to Bob. In their realization, Alice would randomly choose which of the buttons to push by which way her photon happened to go out of a beam-splitter and the result of a photon counting measurement. Bob’s local decoding action was implemented using fast optical switches and measurement. The experiment was conducted for about $10$ minutes, and, using data from photodetectors, they determined that Alice and Bob were winning about $89 %$ of the time when Alice and Bob had access to shared entanglement. This success rate far exceeds what one would expect from the theoretical success probability for a classical strategy, and it is just under the theoretical success probability for the quantum strategy (likely due to slight imperfections in the entangled state).

References

Charles H. Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, and William K. Wootters, Phys. Rev. Lett. 70, 1895 (1993)
Charles H. Bennett and Stephen J. Wiesner, Phys. Rev. Lett. 69, 2881 (1992)
Charles H. Bennett, Peter W. Shor, John A. Smolin, and Ashish V. Thapliyal, Phys. Rev. Lett. 83, 3081 (1999)
R. Prevedel, Y. Lu, W. Matthews, R. Kaltenbaek, and K. J. Resch, Phys. Rev. Lett. 106, 110505 (2011)

About the Author

Mark M. Wilde received his B.S. degree in computer engineering from Texas A&M University in 2002, his M.S. degree in electrical engineering from Tulane University in 2004, and his Ph.D. degree in electrical engineering from the University of Southern California in 2008. Currently, he is a Postdoctoral Fellow at the School of Computer Science, McGill University. He has published about 40 articles and preprints in the area of quantum information processing. His current research interests are in quantum error correction and quantum Shannon theory.