An optical lattice of flux
Ultracold neutral atoms are among the most simple and flexible of quantum many-body systems. As such, they offer the capability to realize strongly interacting systems in their most fundamental form, absent the unwanted complexities that complicate (and sometimes enrich) their solid-state brethren. The question then arises: What classes of systems can be implemented with cold atoms, and of these, which can offer insight beyond that afforded in more conventional systems? In a paper published in Physical Review Letters, Nigel Cooper at the University of Cambridge, UK, proposes an elegant technique to take ultracold atoms to the extreme, where atoms moving about in a lattice potential experience an effective magnetic field with of order a unit flux quanta per lattice site [1]. This is a realm that is inaccessible in conventional materials and promises new types of quantized Hall effects where Landau-level quantization and band-structure effects are intertwined.
Magnetic fields are enigmatic. In our studies we learn the Lorentz force law: in a uniform magnetic field, the force on a moving, charged object is perpendicular to both the magnetic field and the object’s velocity . This doesn’t fit in with our usual intuitive picture of forces derived from gradients of potentials, but instead requires a new type of potential: the electromagnetic vector potential . Like the usual scalar potential , the vector potential is related to the seemingly more physical fields via derivatives: the magnetic field . These potentials are not just mathematical sleights-of-hand; in quantum systems, they take center stage.
In Schrödinger’s wave mechanics, the evolution of a particle’s wave function can be partially understood in terms of its quantum mechanical phase. Usually this phase can be divided into two parts: the dynamic phase acquired in proportion to the particle’s kinetic energy, and the phase from scalar potentials. Each of these accumulates at a rate proportional to the associated energy. If we consider a particle moving in a closed loop, with zero scalar potential, then the dynamic phase acquired upon traversing the loop will tend to zero as the velocity drops to zero.
The phase acquired in a magnetic field is different: it depends on the geometry of the particle’s path. If our loop now encloses a magnetic flux , then the particle will acquire an additional phase proportional to . This interpretation is uncomfortable: somehow the particle has a nonlocal knowledge of the magnetic field everywhere inside the loop. It is more natural to think of the vector potential, in which case the acquired phase is no more than the line-integral of the vector potential around the loop. This leads to the celebrated Aharonov-Bohm effect [2,3] where a charged particle acquires a geometric phase as it moves in the completely field-free region outside an infinite solenoid.
Other physical situations produce geometric phases in which neutral particles can behave as if magnetic fields were present. This concept was introduced to quantum mechanics as Berry’s phase [4] for particles with internal structure (like spin states) for which the energy is dependent on parameters in the Hamiltonian, such as position or momentum. If a particle starts in an eigenstate, it can acquire a geometric phase upon traversing a closed loop in parameter space, provided the “motion” is sufficiently slow that it adiabatically remains in the same eigenstate.
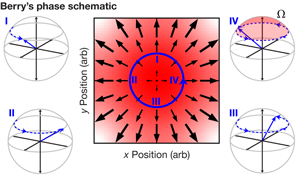
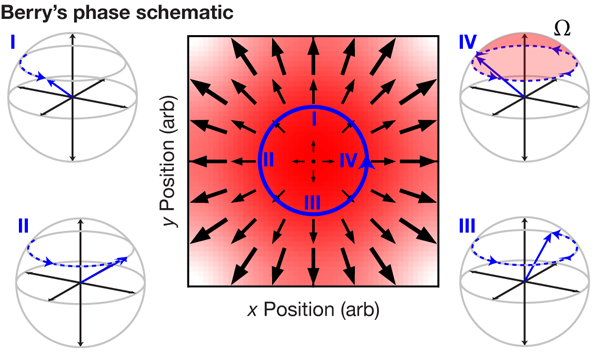
The simplest example of a Berry’s phase is shown in Fig. 1 where a neutral spin- particle is moving in an inhomogenous magnetic field, giving rise to a position-dependent Zeeman shift—the difference in energy between the spin being oriented along or away from the magnetic field. The figure depicts the particle’s trajectory, along with the orientation of its ground state on the Bloch sphere. (This sphere defines the allowed states of a spin- particle.) The particle accumulates a geometric phase of , one-half the solid area traced out on the Bloch sphere as the particle moves in space. Such a phase can be interpreted as arising from a geometric gauge field, in analogy with the electromagnetic vector potential.
Geometric phases are real. A system particularly well suited for observing and studying their effects is a trap of ultracold atoms. In these systems researchers can first construct suitable geometries and then unambiguously measure the result. Geometric phases in neutral atoms were vividly demonstrated at MIT in 2002 when topological phases were directly imprinted into the wave function of a Bose-Einstein condensate (BEC) of sodium atoms in a magnetic field by inverting the orientation of the field. This produced or phase windings leading to vortices in the final wave function [5].
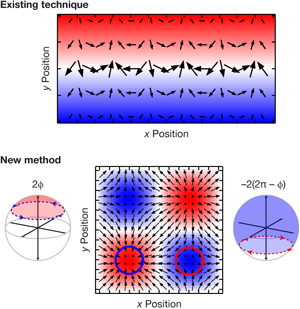
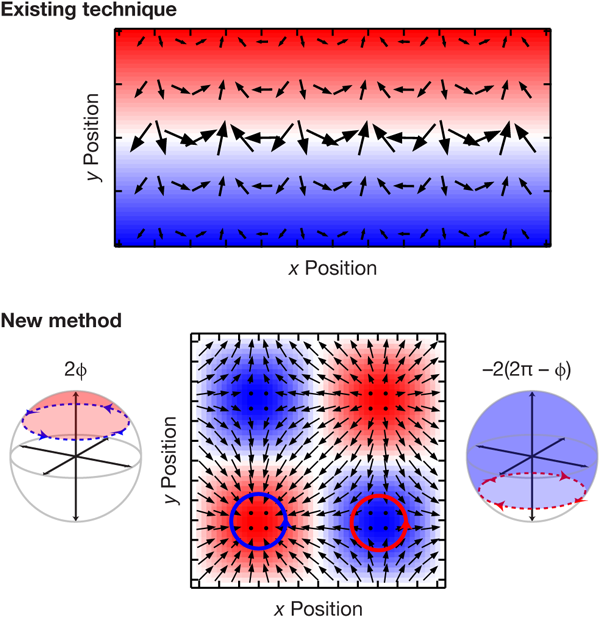
Going beyond this elegant demonstration, the next step is more powerful: constructing configurations where the atomic system obeys a new Hamiltonian containing steady-state gauge fields [6]. Such a system mimics that of a particle in an effective magnetic field [7]. Instead of using a magnetic field to generate a Berry’s phase, these ideas require a laser to couple different internal (spin) states of atoms. Such coupling is formally equivalent to a Zeeman magnetic field, but spatially structured on the scale of the optical wavelength. In our group at NIST, we followed these theory proposals with a series of experiments demonstrating the effective mapping between the Berry’s phase and the electromagnetic vector potential, leading to artificial magnetic and electric fields (see Refs. [8,9] and references therein). The top of Fig. 2 depicts how these ideas lead to large Berry’s phases, and also highlights a key limitation. The illustrated Bloch vector can wind an unlimited number of times around its equator as an atom moves along , but it can tip to the axes of the Bloch sphere when the atom moves along . This implies that we can create large “artificial magnetic fields,” but the maximum magnetic flux passing through the system scales as the length of the system, not its area, making it difficult to scale the artificial field to larger systems.
Cooper proposes a technique to overcome this limitation [1] by creating a specific effective Zeeman field using standing waves of light—a type of lattice. The essence of his proposal is depicted in the bottom of Fig. 2: atoms moving in the optical unit cell experience a Berry’s phase, both as a function of and (see also Ref. [10]). Usually such ideas lead to staggered magnetic fields with equal and opposite sign in neighboring lattice sites, with zero average. The current work overcomes this limitation, allowing for large effective magnetic fields with flux scaling as the system’s area, not its linear extent.
How does this work? The effective electromagnetic vector potential created by this technique has a gauge-dependent singularity called a Dirac string that effectively concentrates magnetic field of one sign to isolated points (with no physical effect). As a result, the effective magnetic field is still staggered, but acquires a nonzero average.
To more intuitively understand how this gives rise to an effective field of the same sign, consider an atom moving along each of the two closed loops depicted in Fig. 2 (bottom). For the left loop, the Zeeman field traces out a circle at the top of the Bloch sphere with a counterclockwise direction, while the right loop traces a circle at the bottom of the Bloch sphere with a clockwise direction. If the top loop acquired a geometric phase , then the bottom loop acquired a phase of from the entire top portion of the Bloch sphere, but with the opposite sign. Since the acquired phase is defined only modulo , these two curves enclose the same effective field.
This seemingly simple observation provides a straightforward path to realize larger effective magnetic fields than have hitherto been possible, yet with a comparatively simple set of lasers. (The pioneering proposals for large in-lattice gauge fields require more numerous lasers [11], and lack the simplicity and elegance of this approach.)
To complete the story, Cooper studied the properties of the lowest Bloch bands in this optical flux lattice and computed the Chern number. (Here, the Chern number enumerates the number of times the wave function’s phase winds by on a path running from one side of the Block band to the other: a loop on the torus). In some cases, the Chern number is , showing that these bands are topologically equivalent to the lowest Landau level (also with Chern number ). Thus fermions completely filling the lowest band will be an integer quantum Hall state with a quantized Hall resistance . The atoms used in cold-atom experiments are typically bosons and do not have a Fermi energy, but at fillings of around one per-lattice site—about one atom per magnetic flux quanta—they are expected to display interaction-driven bosonic fractional quantum Hall states.
Acknowledgments
I would like to thank V. Gurarie and A. Lamacraft for discussions that prepared me to appreciate the current work. I also acknowledge the financial support of the NSF through the PFC at JQI, and the ARO with funds from both the Atomtronics MURI and the DARPA OLE Program.
Correction (29 April 2011): References [8] and [9] were corrected.
References
- N. R. Cooper, Phys. Rev. Lett. 106, 175301 (2011)
- W. Ehrenberg and R. E. Siday, Proc. Phys. Soc. London Sect. B 62, 8 (1949)
- Y. Aharonov and D. Bohm, Phys. Rev. 115, 485 (1959)
- M. V. Berry, Proc. R. Soc. London A 392, 45 (1984)
- A. E. Leanhardt, A. Görlitz, A. P. Chikkatur, D. Kielpinski, Y. Shin, D. E. Pritchard, and W. Ketterle, Phys. Rev. Lett. 89, 190403 (2002)
- R. Dum and M. Olshanii, Phys. Rev. Lett. 76, 1788 (1996)
- G. Juzeliūnas, P. Öhberg, J. Ruseckas, and A. Klein, Phys. Rev. A 71, 053614 (2005)
- Y.-J. Lin, R. L. Compton, K. Jiménez-García, W. D. Phillips, J. V. Porto, and I. B. Spielman, Nature 462,628 (2009)
- Y.-J. Lin, R. L. Compton, K. Jiménez-García, W. D. Phillips, J. V. Porto, and I. B. Spielman, Nature Phys. (2011)
- A. M. Dudarev, R. B. Diener, I. Carusotto, and Q. Niu, Phys. Rev. Lett. 92, 153005 (2004)
- D. Jaksch and P. Zoller, New J. Phys. 5, 56 (2003)