Quantum simulation hits the open road
One of the most important practical applications of a quantum computer would be the simulation of other quantum systems. Until now, the possibility of an accurate simulation had been rigorously demonstrated only for closed quantum systems—those with no decoherence or dissipation due to interactions with an environment. In Physical Review Letters, Martin Kliesch of the Free University of Berlin and the University of Potsdam, Germany, and his colleagues have shown rigorously that open quantum systems—those which interact with an environment—can also be efficiently simulated with quantum computers [1]. This opens up the potential impact of quantum computers to important applications in condensed-matter physics, quantum chemistry, and even biology.
Simulating many-body quantum systems is hard. For many interacting quantum many-body systems, the best-known algorithms for their exact simulation on a classical computer require computational resources that grow exponentially with the number of particles. This inefficient scaling puts exact simulation of important phenomena that involve many particles, such as high-temperature superconductivity, out of our computational reach.
Richard Feynman was one of the first to suggest that perhaps this “bug” could be a “feature” [2]: quantum systems may be hard to simulate on classical machines, but perhaps they could efficiently simulate each other. This idea was taken further by David Deutsch [3], who showed that one could define a fully quantum model of computation and outlined how Feynman’s quantum simulation ideas might be put into practice.
In a quantum computer, coherent logic gates act upon a register of quantum bits, or qubits. These gates are unitary, meaning that the quantum states are transformed coherently and reversibly. Quantum computers are thought to have greater computational power than classical computers since there are problems, most famously that of factoring integers, that can be solved efficiently on a quantum computer, but for which no efficient classical algorithm has been found. Intensive research is underway worldwide to develop physical technologies for quantum computers that are scalable to practically important sizes.
Until now, however, rigorous analyses of quantum simulation schemes [4,5] have been confined to closed quantum systems, not the open systems that describe many real-life situations. We say a system is closed when it has no interaction with any other system around it. Closed systems are isolated, cut off from the universe. Systems evolve in time unitarily, according to Schrödinger’s equation, where the detailed physics of the system is captured by the Hamiltonian, the operator in which the details of system energies and interactions are recorded.
The study of closed systems has a central role in quantum physics, and we can model many important effects this way. For this reason, closed quantum dynamics is often the only type of quantum dynamics studied by undergraduate students. However, the systems we see in nature are never closed. They interact with particles around them, and in many cases, their physical behavior is dominated by the effect of these interactions.
Schrödinger’s equation is not enough to describe the dynamics of open quantum systems: new techniques are required. Of these, arguably the most important is the Louvillian master equation [6], which can be thought of as the open-quantum-system equivalent of Schrödinger’s equation. The Louvillian is an operator that plays an analogous role to the Hamiltonian, specifying interactions, but also expressing dissipation and decoherence processes due to the environment.
Although quantum simulation was one of the first applications proposed for a quantum computer, detailed methods for doing it were not considered until the mid-nineties, when Seth Lloyd presented a suite of techniques to accomplish this [7]. In many systems that we might want to simulate, all components simultaneously interact with one another. A realistic quantum computer, however, will only act on a few of the corresponding qubits at a time, and then only in discrete quantum gates. Lloyd suggested that the complex dynamics of an interacting many-particle system might be broken down into simpler slices, each consisting of, say, just a single two-party interaction that can be directly simulated by the unitary gates of a quantum computer. The mathematical tool that he used to show this is called the Suzuki-Trotter theorem.
The Suzuki-Trotter theorem [8,9] is a mathematical result about unitary transformations. As such it can be directly applied to the dynamics of closed quantum systems, since such systems evolve unitarily. The theorem says that to simulate a closed many-body system with many pairwise interactions one can instead switch on each of the interactions in turn, rapidly switching stroboscopically between the individual interactions. The faster the stroboscopic switching the better the approximation, leading, in the limit of infinitely fast switching, to a perfect reproduction of the original dynamics.
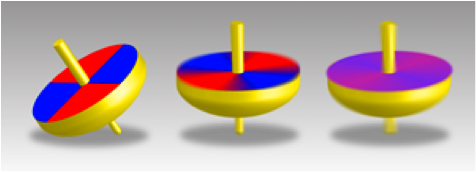
The effect is very similar to a famous optical illusion. If we paint a spinning top in segments of red and blue and spin the top fast, to our eye, the individual colors merge together, so we can only see a shade of purple, even though no part of the top is purple at all (see Fig. 1).
Kliesch et al. show that the Suzuki-Trotter theorem can be generalized to the dynamics of open quantum systems. They show that the stroboscopic trick is also effective for Louvillian dynamics, obtaining rigorous bounds on the error in the approximation. These results prove that open quantum systems may be efficiently simulated on a quantum computer. Now even more research activities, including mesoscopic physics, photosynthesis, and noncryogenic quantum chemistry, can be added to the list of scientific areas for which a quantum computer could prove a revolutionary research tool.
References
- M. Kliesch, T. Barthel, C. Gogolin, M. Kastoryano, and J. Eisert, Phys. Rev. Lett. 107, 120501 (2011)
- R. Feynman, Int. J. Th. Phys. 21, 467 (1982)
- D. Deutsch, Proc. R. Soc. London. A 400, 97 (1985)
- D. Aharonov and A. Ta-Shma, in Proceedings of the Thirty-Fifth Annual ACM Symposium on Theory of Computing, San Diego, CA, June 9-11, 2003 (ACM Press, New York, 2003)[Amazon][WorldCat]
- D. W. Berry, G. Ahokas, R. Cleve, and B. C. Sanders, Commun. Math. Phys. 270, 359 (2007)
- G. Lindblad, Commun. Math. Phys. 48, 119 (1976)
- S. Lloyd, Science 273, 1073 (1996)
- M. Suzuki, J. Math. Phys. 26, 601 (1985)
- H. F. Trotter, Proc. Am. Math. Soc. 10, 545 (1959)