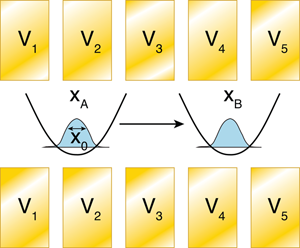
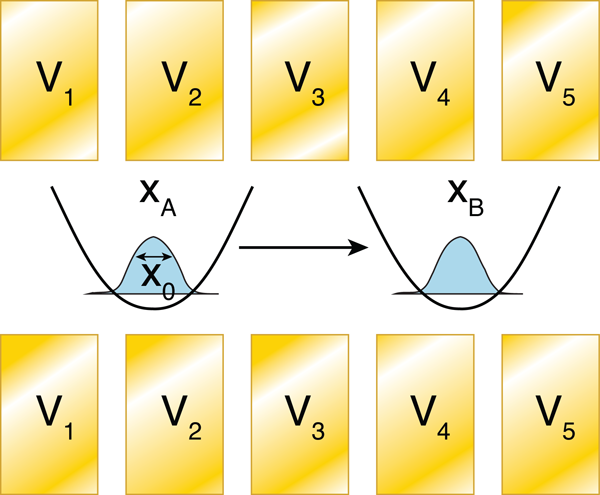
Moving Traps Offer Fast Delivery of Cold Ions

Christian Roos

Viewpoint

Moving Traps Offer Fast Delivery of Cold Ions

Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences, A-6020 Innsbruck, Austria

August 20, 2012• Physics 5, 94

Two separate experiments have demonstrated the fast transport of trapped ions using trapping potentials that trace out the path for the ions to follow.

Figure caption — **Figure 1:** In a segmented ion trap, approximately harmonic potentials can be created at any point along the symmetry axis of the trap by a suitable combination of voltages $V_{i}$ applied to the trap electrodes. Transport from position $x_{A}$ to $x_{B}$ is accomplished by applying temporal voltage wave forms to the electrodes that translate the potential without modifying its shape. The final state of the trapped ion is the same as its initial state with a wave function size of $x_{0}$ .

Quantum physics experiments with trapped atoms or ions often require that the particles occupy the lowest quantum state of the trapping potential. This presents a challenge when the particles need to be moved to a different location in order to perform, for example, a quantum computation. Previous experiments succeeded in transporting trapped ions, albeit slowly, by modifying the trapping potential in such a way that the particles remain in the lowest energy state throughout the transport. Two groups of researchers have now succeeded in considerably speeding up ion transport in microfabricated ion traps. As described in separate papers in Physical Review Letters [1,2], the teams propelled the motion by strongly exciting the ions for a short time before returning them to their initial state at the end of the transport. The demonstration of fast transport that preserves the motional state of trapped ions opens up interesting perspectives in the context of quantum information processing with trapped ions in multiplexed ion traps.

How can a trapped particle be transported over a distance without perturbing its motional state? Let’s assume that the particle is trapped in a harmonic potential well $V (x, t) = \frac{1}{2} m ω^{2} (x - x^{*} (t))^{2}$ , whose center $x^{*} (t)$ we want to displace from location $x_{A}$ to location $x_{B}$ . An easy solution is to transport the particle adiabatically by making slow temporal changes to the trapping potential so that the particle’s wave function can adjust to keep its center always at the minimum of the potential. This approach is too slow for quantum computing applications, as the particle’s acceleration has to stay well below $x_{0} ω^{2}$ , where $x_{0}$ is the ground-state size of the particle and $ω$ the particle’s oscillation frequency.

There are, however, other strategies that allow for much faster transport if one drops the requirement of preserving the particle’s quantum state during the whole transport. As an extreme example of a diabatic (energy-transferring) process, rapid switches in the potential well can transport the particle within half an oscillation period. Specifically, an instantaneous displacement of the potential well from $x_{A}$ to the midpoint of the line between $x_{A}$ and $x_{B}$ would give the particle enough energy so that it can oscillate from $x_{A}$ to $x_{B}$ (like a ball rolling from one side of a valley to another). When the particle arrives at $x_{B}$ , the potential well could once again be instantaneously displaced to the endpoint $x_{B}$ . This second step takes out all the potential energy given to the particle in the first step and returns the particle to its initial state.

The above protocol is, however, impractical for two reasons. First, if the distance $L = x_{B} - x_{A}$ is much larger than the ground-state size $x_{0}$ , then a huge amount of energy is transferred to the particle, exciting it to a motional state with about ( $L / x_{0})^{2}$ quanta. Under these conditions, even minute fluctuations of the experimental control parameter would prevent the particle from ending up in the desired final quantum state. Second, instantaneous potential changes are not achievable. The time required to switch the potential shape is limited by the finite bandwidth of the experimental hardware.

The recent experiments [1,2] from Ryan Bowler and colleagues at NIST in Boulder, Colorado, and Andreas Walther and colleagues at the University of Mainz, Germany, followed an intermediate strategy for realizing a fast, diabatic quantum transport of ions. Both research groups confined ions in microfabricated linear Paul traps, which use a combination of static and radio-frequency electric fields to create approximately harmonic potentials. The location of the potential minimum along the trap axis can be controlled by adjusting the dc voltages applied to different electrode segments of the trap (see Fig. 1). The research teams realized ion transport by programming wave form generators to vary the electrode voltages so that the trapping potential translates from $x_{A}$ to $x_{B}$ . The shape of the potential well does not change during this process, but in contrast to adiabatic transport, the center of the wave function cannot follow the fast movement of the center of the trap. This transfers kinetic energy to the ion, which, at the end of the transport, is taken out again.

To demonstrate fast diabatic transport, the Boulder group laser-cooled a single ${Be}^{+}$ ion close to the ground state of the potential, transported the ion over $370$ micrometers ( $μ m$ ) in $8$ microseconds ( $μ s$ ) and demonstrated that the final quantum state was still very close to the ground state for suitably chosen voltage wave forms [1]. The Mainz group reported similar results with a trapped ${Ca}^{+}$ ion transported over $280 μ m$ in about $4 μ s$ [2]. What makes these numbers significant is the fact that the ions moved within about ten oscillation periods over a distance of about $30, 000$ times the spatial width of the particle’s wave function.

These experiments are not the first to report diabatic transport without significant heating. Previous work demonstrated the collective transport of ultracold atoms trapped in optical tweezers [3]. The advantage of trapped ions over atoms is that the motional quantum state of an ion can be examined in great detail by laser pulses that coherently couple motional states to long-lived internal states of the ion. By a fluorescence measurement to detect the internal state of the ion, both groups could demonstrate that their ions gained less than an average of $0.1$ motional excitations in the transport process. Moreover, both groups showed that the coherence of motional superposition states is preserved by the transport process.

The demonstration of fast shuttling operations is exciting in view of quantum information processing with large numbers of trapped ions arranged in a crystal lattice structure. Each ion encodes a quantum bit of information, and laser pulses couple the ion qubits and ion motion in quantum logic gates. As it seems unlikely that information processing can be achieved with “ion crystals” of more than a few tens of ions, strategies for going beyond that limit envision several smaller ensembles of ions that are either split up and recombined or linked up by exchange of photons [4,5]. Kielpinski et al. [4] proposed a device consisting of a trap with multiple storage and processing zones between which ions are distributed. This approach requires fast processes for shuttling and splitting ion crystals into smaller units. While in previous experiments, ion transport was much slower than quantum gate operations, in the latest experiments both happen on comparable time scales, thus speeding up any transport-dependent computational process. In addition, Bowler et al. [1] demonstrate splitting of a two-ion crystal with low motional heating in about $100$ oscillation periods. What still needs to be done is to extend the work to mixed-species ion crystals, where fast dynamic changes to the potential can couple more easily to multiple vibrational modes.

The reported results are also good news for a project aimed at creating nitrogen-vacancy centers in diamond by ion implantation [6]. The idea is to use rapid switching of trapping potentials to accelerate a ground-state cooled $N^{+}$ ion out of an ion trap and then direct it with high spatial resolution into a diamond target. In this respect, the excellent control over the motional state demonstrated in fast transport is positive evidence for the idea that the spatial coherence can be maintained when an ion is ejected from a trap and focused into a piece of diamond.

References

R. Bowler, J. Gaebler, Y. Lin, T. R. Tan, D. Hanneke, J. D. Jost, J. P. Home, D. Leibfried, and D. J. Wineland, ”Coherent Diabatic Ion Transport and Separation in a Multizone Trap Array,” Phys. Rev. Lett. 109, 080502 (2012)
A. Walther, F. Ziesel, T. Ruster, S. T. Dawkins, K. Ott, M. Hettrich, K. Singer, F. Schmidt-Kaler, and U. Poschinger, ”Controlling Fast Transport of Cold Trapped Ions,” Phys. Rev. Lett. 109, 080501 (2012)
A. Couvert, T. Kawalec, G. Reinaudi, and D. Guéry-Odelin, “Optimal Transport of Ultracold Atoms in the Nonadiabatic Regime,” Euro. Phys. Lett. 83, 13001 (2008)
D. Kielpinski, C. Monroe, and D. Wineland, “Architecture for a Large-Scale Ion-Trap Quantum Computer,” Nature 417, 709 (2002)
L.-M. Duan, B. B. Blinov, D. L. Moehring, and C. Monroe, “Scalable Trapped Ion Quantum Computation with a Probabilistic Ion-Photon Mapping,” Quant. Inform. Comput. 4, No. 3, 165 (2004)
J. Meijer et al., “Concept of Deterministic Single Ion Doping with Sub-nm Spatial Resolution,” Appl. Phys. A 83, 321 (2006)

About the Author

Christian Roos is a senior scientist at the Institute for Quantum Optics and Quantum Information, Innsbruck, Austria. He received his Ph.D. in physics from the University of Innsbruck and has worked as a Marie-Curie fellow at the Laboratoire Kastler-Brossel at Ecole Normale Supérieure, Paris. His current research focuses on trapped-ion based quantum information processing and precision spectroscopy.