Spin-Orbit Coupling Comes in From the Cold
One thriving area of cold-atom research is the development of techniques allowing dilute gases at nanokelvin temperatures to reproduce phenomena central to other fields, such as solid-state or nuclear physics. By precisely tuning properties such as density, temperature, and interaction strength, one can gain unprecedented quantitative insights into many physical processes. As reported in Physical Review Letters, two groups of researchers, Pengjun Wang at Shanxi University in China and colleagues [1], and Lawrence Cheuk from the Massachusetts Institute of Technology, Cambridge, and colleagues [2], have expanded the cold-atom experimental toolbox by engineering a system of fermionic atoms in which lasers induce strong spin-orbit coupling. One can envision that this technique may be combined with Feshbach resonances [3] (which control the interatomic interactions) and optical lattices (which mimic the lattices in real materials), enabling the production of exotic states found in condensed-matter systems such as topological insulators. Even more importantly, one hopes to realize novel states of matter (e.g., “fractional topological insulators”), which are anticipated by many theoretical studies but are hard to create and analyze experimentally.
Spin-orbit coupling refers to the interaction between the spin and motion degrees of freedom of an electron. A simple illustrative model is a 2D electron gas in the presence of a uniform electric field perpendicular to the plane. According to special relativity, the electric field is seen as a magnetic field in the moving electrons’ frame of reference. The magnetic field’s strength and direction depend on the velocity of the electron, producing a correlation between the electrons’ momenta and their spin states. At field strengths available in the laboratory this correlation can generally be neglected for any reasonable electronic velocities. However, strong spin-orbit coupling can be found in materials that contain heavier elements and lack inversion symmetry: the electron motion becomes relativistic near the ion cores, and the local electric field can be strong.
While these relativistic effects can couple an electron’s spin to its motion, coupling the spin and the center-of-mass motion of a neutral atom presents a challenge. In order to introduce spin-orbit coupling in neutral atomic gases, both Wang et al. and Cheuk et al. turned to a technique pioneered with bosonic Rubidium atoms [4]. While spin-orbit-coupled Bose gases have generated much excitement, Fermi gases hold even more promise. Due to the Pauli exclusion principle, fermions occupy a large number of momentum states, and are therefore sensitive to global (topological) features of the band structure. Conversely, Bose-Einstein condensation typically occurs in one or two single-particle states. Spin-orbit-coupled fermionic gases would thus provide ways to explore a much richer phenomenology.
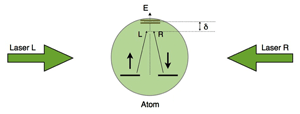
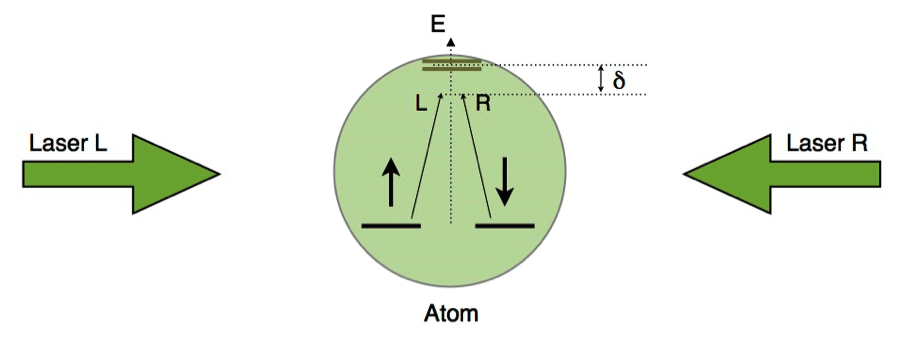
The basic principles of the technique are illustrated in Fig. 1. The experimentalists single out two among the many internal hyperfine atomic states, labeled and in analogy with the electronic spin. Two counterpropagating laser beams are introduced to couple these states by a resonant stimulated two-photon Raman transition: by absorbing a photon from the left beam, and emitting it into the right beam, a atom will flip into the state. Since in the process the atom receives a momentum kick, this provides a mechanism by which spin and momentum become coupled. In these experiments, the symmetries are different from our 2D example of electrons in a field and from spin-orbit coupling in solids: here, a unidirectional spin-orbit coupling is realized, where only the component of the momentum is coupled to spin.
Such symmetry differences can be viewed as either a blessing (allowing one to study novel physics) or a curse (making it difficult to model the physics most relevant for solid-state physics). Nevertheless, the current geometry can lead to exciting effects. For example, near a Feshbach resonance the fermions should pair to form a superconducting state similar to that seen in spin-orbit-coupled semiconducting wires [5]. The analogy becomes even stronger if an optical lattice is used to break the atomic cloud into an array of wires [6]. Such wires are expected to exhibit Majorana edge modes, which can be used for quantum computation (see 15 March 2010 Viewpoint).
There are a number of technical difficulties in using lasers to couple atomic motion and hyperfine states: photons can only flip electronic or nuclear spins when they are coupled to electronic motion. Thus, to allow the transition from to , experimentalists must tune the lasers near a multiplet of excited states (see Fig. 1). The detuning from resonance ( ), must be of the same order of magnitude as the fine structure splitting of that multiplet. Unfortunately, close to an optically allowed transition, one must contend with resonant absorption, which heats the gas. The crucial figure of merit is the ratio of the linewidth of the resonance to the fine structure splitting. This ratio is larger for lighter elements, which will therefore suffer more heating: bosonic rubidium-87 is more favorable than fermionic potassium-40, which in turn is more favorable than fermionic lithium-6.
Wang et al. carried out their studies using potassium-40. They looked at equilibrium properties (measuring the thermal occupation of the various momentum and spin states) as well as dynamics (monitoring the time evolution of the spin populations starting from a polarized state) and measured the energy-momentum dispersion relation (using momentum-resolved radio-frequency spectroscopy, a technique related to angle-resolved photoemission spectroscopy). Through these studies they deliver a quantitative, coherent, and very intuitive picture of spin-orbit coupling in this noninteracting Fermi gas.
Cheuk et al. instead focused on lithium-6. This was a bold choice: as previously mentioned, lithium has an unfavorable ratio of fine structure splitting to linewidth. In fact, prior to this study the common wisdom was that inelastic light scattering would make such a study impractical. The authors came up with an ingenious approach to circumvent this problem: they worked with four atomic states, and used radio waves to drive transitions from two “reservoir” states into two spin-orbit-coupled states. They controlled the heating by keeping the population of the spin-orbit-coupled states low. By monitoring the transition rate as a function of the radio frequency, they were able to map out the dispersion of the spin-orbit-coupled states. Their study provided a comprehensive view of spin-orbit coupling in the absence of interparticle interactions. It remains to be seen if a similar strategy will allow the study of physics where such interparticle interactions are important.
The approach of Wang et al. and Cheuk et al. may prove valuable for using cold gases to recreate and explore the physics of topological insulators and superconductors. By providing new ways to investigate spin-orbit physics, these studies could also have a profound impact on the development of spintronic devices operated by spin instead of charge (see 15 June 2009 Trend).
References
- P. Wang, Z-Q. Yu, Z. Fu, J. Miao, L. Huang, S. Chai, H. Zhai, and J. Zhang, ”Spin-Orbit Coupled Degenerate Fermi Gases,” Phys. Rev. Lett. 109, 095301 (2012)
- L. W. Cheuk, A. T. Sommer, Z. Hadzibabic, T. Yefsah, W. S. Bakr, and M. W. Zwierlein, ”Spin-Injection Spectroscopy of a Spin-Orbit Coupled Fermi Gas,” Phys. Rev. Lett. 109, 095302 (2012)
- C. Chin, R. Grimm, P. Julienne, and E. Tiesinga, “Feshbach Resonances in Ultracold Gases,” Rev. Mod. Phys. 82, 1225 (2010)
- Y.-J. Lin, K. Jimnez-Garca, and I. B. Spielman, “Spin Orbit-Coupled Bose Einstein Condensates,” Nature 471, 83 (2011)
- V. Mourik, K. Zuo, S. M. Frolov, S. R. Plissard, E. P. A. M. Bakkers, and L. P. Kouwenhoven, “Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices,” Science 336, 1003 (2012); J. R. Williams et al., “Signatures of Majorana Fermions in Hybrid Superconductor-Topological Insulator Devices,” arXiv:1202.2323 (2012); M. T. Deng, C. L. Yu, G. Y. Huang, M. Larsson, P. Caro, and H. Q. Xu, “Observation of Majorana Fermions in a Nb-InSb Nanowire-Nb Hybrid Quantum Device,” arXiv:1204.4130 (2012); A. Das. Y. Ronen, Y. Most, Y. Oreg, M. Heiblum, and H. Shtrikman, “Evidence of Majorana Fermions in an Al-InAs Nanowire Topological Superconductor, arXiv:1205.7073 (2012)
- Y. Liao, A. S. C. Rittner, T. Paprotta, W. Li, G. B. Partridge, R. G. Hulet, S. K. Baur, and E. J. Mueller,“Spin-Imbalance in a One-Dimensional Fermi Gas,” Nature 467, 567 (2010)