Exploring the Neural Manifold

Olivier Marre; Alain Destexhe

Viewpoint

Exploring the Neural Manifold

Olivier Marre

Institut de la Vision, UMRS 968 UPMC, INSERM, CNRS U7210, CHNO Quinze-Vingts, F-75012 Paris, France

Alain Destexhe

Unit for Neuroscience, Information and Complexity (UNIC), CNRS, Gif sur Yvette, France

January 28, 2013• Physics 6, 11

A new way to characterize the encoding of signals from the retina defines a distance between different stimuli according to the similarity of their neural responses.

Figure caption — **Figure 1:** Two different stimuli, labeled $s_{1}$ and $s_{2}$ , were presented to a salamander retina. This is schematically shown here as grey patches on light and dark backgrounds, but Tkačik *et al.* used sequences of flickering light. They triggered two different sets of neural responses $σ$ to repeats of the same stimuli. Out of these repeats, a distance $D_{ret}$ between $s_{1}$ and $s_{2}$ was computed as the difference between $P (σ | s_{1})$ and $P (σ | s_{2})$ . The bottom right panel shows the matrix of distance for different pairs of stimuli indexed by $t [s]$ . The upper diagonal shows the Euclidian distance between the stimuli, the lower diagonal the Dret distance estimated from the retinal acitivity.

Anyone who has experienced change blindness (in which a large difference between two images goes unnoticed [1]) knows that while our brain is supposed to efficiently process the sensory inputs from our natural environment, it can be tricked by well-designed stimuli. In the visual system, this is best reflected by optical illusions in which two physically different stimuli appear identical. For example, the perceived brightness of an area can be greatly influenced by the luminance of the surrounding areas: a gray patch on a dark background can appear as bright as a darker patch on a bright background [2]. These illusions suggest that physically different stimuli will trigger identical responses in a part of the visual system. Searching for the neural basis of such illusions is a major challenge in sensory neuroscience. Some researchers have found that perceived illusions can be reflected in the firing rate of single neurons [3] or populations of neurons [4].

However, a conceptual barrier remains. How do we know if the responses of a population of neurons to two different stimuli are the same? For instance, by comparing the firing rates of the recorded neurons, we assume they contain all the information about the stimulus, an assumption that might be wrong—or insufficient. If we were able to define an objective measure of difference between neuronal patterns, we could determine which stimuli evoke similar responses. A physical stimulus and its illusory percept should be very close in this neural metric. In a paper in Physical Review Letters, Gašper Tkačik at the Institute of Science and Technology, Austria, and colleagues report their theoretical development and experimental study of a new kind of neural metric for characterizing how different two stimuli are in terms of the response of a population of neurons in the retina [5].

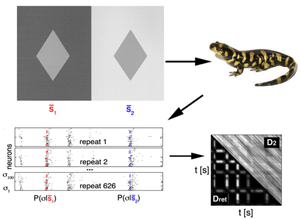
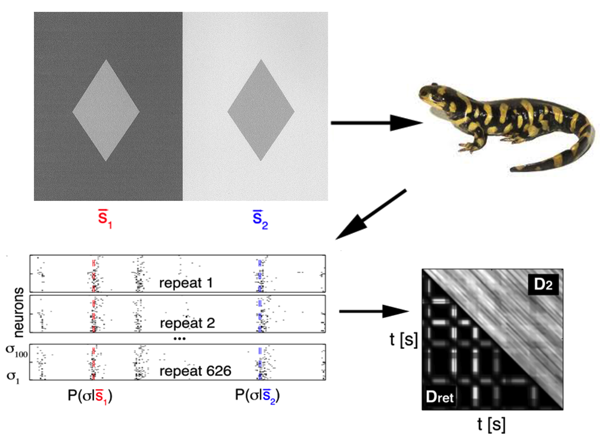
To achieve this, they used data simultaneously recorded from $100$ neurons in the retina of a salamander (a classical model to study neural coding in the retina), while presenting different sequences of flickering light (Fig. 1). Since the relation between a stimulus and the neural response is stochastic, their first step was to obtain an estimate of the conditional probability distribution $P (σ | s)$ , which quantifies the probability that the neural pattern $σ$ is emitted if stimulus $s$ is presented. $σ$ is represented by a binary word with a $1$ for each neuron that emitted a spike, and $0$ for the ones staying silent. This distribution cannot be sampled empirically, so they used a maximum-entropy procedure (stimulus-dependent maximun entropy, or SDME model), developed in detail previously [6], which constructs $P (σ | s)$ ) distributions based on the experimental data. This model predicts the probability of a spike pattern from a weighted sum of the stimulus, the activity of each cell, and the joint activity of pairs of neurons. Using the probability distributions obtained from the model, they defined the retinal distance $D_{ret}$ between the stimuli as the distance between the distributions of responses elicited. This latter is quantified using a symmetrized version of the Kullback-Leibler (KL) divergence, a classical measure to compare two distributions: $D_{KL} (P_{1}, P_{2})$ measures how much information is lost when approximating $P_{2}$ with $P_{1}$ .

The advantage of using $D_{K L}$ is that this measure is relatively agnostic about the exact nature of the neural code: it does not assume that all the information about the stimulus is contained in the average firing rate, or in the timing of the spikes, but takes into account the full distribution of the neural response.

This definition allows the authors to calculate a distance between each pair of stimuli. In a second step, they computed the “distance matrix” between all stimuli, $D_{ret} (s_{i}, s_{j})$ . Such a distance is hard to visualize, so they used a method called multidimensional scaling (MDS) that makes each stimulus correspond to a point in a low-dimensional space, such that the Euclidian distance between the points approximates $D_{ret}$ .

This procedure tells them whether this complex neural metric can be projected in a low-dimensional space, where it is more easily interpretable. In the retina dataset, they found that the two first modes (where the first mode is essentially the firing rate of the neurons) already capture most of the metric in stimulus space. They even build a model that predicts the distance $D_{ret}$ between stimuli from their projections onto two vectors.

These findings show that this large population of neurons, although initially high dimensional, extracts only a few components from the stimulus. This dimensionality reduction was found before for single neurons, using techniques such as spike-triggered covariance analysis, for example [7], showing that each neuron can divide the space of possible stimuli into the ones that evoke the spike and the ones that don’t. The novelty of the approach of Tkačik et al. is to take into account the whole interacting population, rather than single neurons. One might have thought that the different neurons would each separate the stimulus space into distinct subspaces, so that reading the different neurons would increase the information about the stimulus exponentially. However, here it is shown that this population of neurons is very redundant, since its sensitivity can be reduced to two components.

These two components provide an important insight into the changes in the stimulus that the neural population can detect, as well as the ones it cannot. Over the time course of the stimulus, the method of Tkačik et al. predicts that some fluctuations added to the stimulus should not change the retinal response, while others, sometimes smaller, would.

The implications of this work are potentially important. First, it provides methods to investigate how populations code for neural stimuli by taking into account the whole population, not just single neurons. Second, it allows quantifying what aspects of stimulus space are encoded and gives a metric for such quantification. Of course, there are some limitations in this approach. The entire definition of the metric relies on a model connecting the stimulus to the response, and it gives relevant results only as long as this model is a good one. In the present case, the model has been tested and gives a faithful prediction of the retinal response [6]. But for more complex stimuli, or other structures, it is not yet clear how well the same model would perform, and significant extensions might be needed. Nevertheless, this approach is an important step in defining a metric on stimulus space based on a neural network response. It becomes possible to look for the most singular points of this metric, where small deviations will trigger large changes in the neural response. Designing stimuli to probe these singular points would, in fact, be a good way to test the validity of the model.

This neural metric will also have interesting applications in other modalities, especially when there is no natural distance between stimuli, like in olfaction. Finally, it can also have applications to the motor system, and in particular, to neuroprotheses (artificial legs or arms controlled by neural activity), where the key is precisely to define a neural-based distance between motor actions.

References

D. J. Simons and C. F. Chabris, “Gorillas in Our Midst: Sustained Inattentional Blindness for Dynamic Events,” Perception 28, 1059 (1999)
D. Purves, S. M. Williams, S. Nundy, and R. B. Lotto, “Perceiving the Intensity of Light,” Psychol. Rev. 111, 142 (2004)
A. F. Rossi, C. D. Rittenhouse, and M. A. Paradiso, “The Representation of Brightness in Primary Visual Cortex,” Science 273, 1104 (1996)
D. Jancke, F. Chavane, S. Naaman, and A. Grinvald, “Imaging Cortical Correlates of Illusion in Early Visual Cortex,” Nature 428, 423 (2004)
G. Tkačik, E. Granot-Atedgi, R. Segev, and E. Schneidman, “Retinal Metric: A Stimulus Distance Measure Derived from Population Neural Responses,” Phys. Rev. Lett. 110, 058104 (2013)
E. Granot-Atedgi, G. Tkačik, R. Segev, and E. Schneidman, “Stimulus-Dependent Maximum Entropy Models of Neural Population Codes,” arXiv:1205.6438 (2012)
A. L. Fairhall, C. A. Burlingame, R. Narasimhan, R. A. Harris, J. L. Puchalla, and M. J. Berry 2nd, “Selectivity for Multiple Stimulus Features in Retinal Ganglion Cells,” J. Neurophysiol. 96, 2724 (2006)

About the Authors

Olivier Marre is a research fellow at the Vision Institute (UPMC, INSERM, CNRS) in Paris, France. He completed his Ph.D. in 2008 in the UNIC laboratory (CNRS), studying the visual cortex, and then worked as a postdoctoral researcher at Princeton University on neural coding in the retina. Since then, his research interests have focused on population coding in the vertebrate retina.

Alain Destexhe got a B.Sc. at the University of Brussels in 1986, then a Ph.D. in 1992 after a military service interruption. He was then postdoc for three years at the Salk Institute (La Jolla, USA) and from 1995 to 2000, he was Assistant Professor at Laval University (Quebec, Canada). In 2000 he joined the CNRS as a Research Director (Gif sur Yvette, France), where he leads a team of researchers working at the interface between biophysics and neuroscience.