Diamond Spins Shining Bright
The quantum internet of the future could take many forms, but its core components will be quantum bits (qubits) that can store information and qubits that can carry information [1,2]. Atom-sized defects in diamond called silicon vacancy centers are promising candidates as the storage component: they possess a single spin whose quantum state (such as a superposition between “up” and “down”) could encode information. This stored information can also be precisely imprinted on the light the defects emit when excited optically. Independent research groups led by Fedor Jelezko at Ulm University in Germany [3] and by Mete Atatüre at Cambridge University in the UK [4] have now measured the coherence time of the spin on a negatively charged silicon vacancy (SiV) center, a key quantity determining how long the coherent superposition of up and down states can be maintained. Although the measured coherence time is only on the order of tens of nanoseconds (ns), a number of strategies exist to increase it to the point that SiV centers could be viable quantum internet components.
For all candidate qubits, a tradeoff exists between better and faster control and a long coherence time. The spin states of ions floating in vacuum have a coherence time approaching minute [5] (see 24 November 2014 Viewpoint), but rotating them is a slow process. In comparison, electron spin states on semiconductor quantum dots can be quickly rotated electrically or optically, but the best coherence times seen so far are typically less than microseconds [6]. Spin qubits associated with defects in diamond lie somewhere in the middle of these two extremes: Because diamond has a large band gap, there aren’t many states that a spin qubit could decay into, and, on some defects, the spin’s state can be quickly rotated with light. Most research so far has focused on spin states associated with nitrogen vacancy (NV) centers, in which a nitrogen atom substitutes for a carbon atom that sits next to a vacant atom site. The spin states of NV centers have coherence times of roughly microseconds and can be controlled even at room temperature [7].
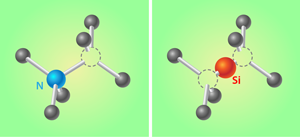
In the SiV center, Si substitutes for one of the missing carbon atoms. Like the NV center, the negatively charged SiV center carries an electronic spin in its ground state. But despite similarities between the two defects, there are important differences: The N atom and its adjacent vacancy break the inversion symmetry of the diamond crystal. In contrast, the Si atom in the SiV center sits halfway between two vacant carbon sites (Fig. 1). Because this configuration is symmetric under inversion, the SiV center is relatively insensitive to stray electric field fluctuations and, as a result, photons emitted from the SiV center have a narrow linewidth around a bright peak [8]. This feature is desirable for quantum communications applications, such as preparing indistinguishable photons that can be entangled. Finally, compared to NV centers, SiV centers are much less likely to lose energy by exciting vibrations (phonons) in the surrounding diamond lattice.
Despite its many attributes for quantum communication, the SiV center has a handicap: its ground state consists of two degenerate states with different orbital configurations. The defect is therefore unstable towards a lattice distortion, known as the static Jahn-Teller (JT) effect. Moreover, interactions between electrons on the SiV center and phonons in the lattice cause the SiV center to switch rapidly between its two ground-state orbitals, a phenomenon known as the dynamic JT effect. Because the spin state is weakly coupled to the orbital state, the JT effect is expected to limit the spin coherence time of the SiV center, but to what extent has been largely unknown.
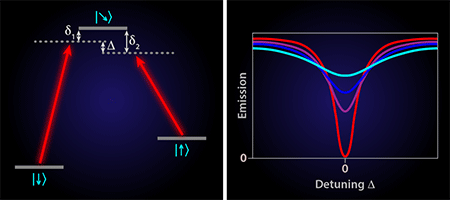
To measure the spin coherence time of a single SiV center, Jelezko and his collaborators [3] and Atatüre and his collaborators [4] performed a technique known as coherent population trapping (CPT), which has been used to study NV centers [9]. The scheme uses two phase-locked laser fields to couple the two ground-state spin states (up and down) to a common excited state (Fig. 2, left). For a given relative phase and amplitude of the two exciting laser fields, the system will be trapped into a “dark state,” which is a specific coherent superposition of the two ground states. This dark state cannot be excited optically and photon emission is suppressed, causing a narrow dip in the excitation spectrum when the lasers are tuned to a “two photon resonance” (the point at which a photon can be virtually absorbed and reemitted without energy loss). Since spin decoherence tends to mix the dark state with other states and makes the dip more shallow and broader, one can infer the coherence time between the two spin states from the dip’s depth and width (Fig. 2, right). The groups performed CPT on SiV centers in diamond to determine a spin coherence time, [3] and [4] at a temperature of around . (The asterisk in indicates the coherence time was averaged over the time of the measurement.)
The new measurements verify that the SiV center has a spin in its ground state—something that was hinted at by earlier experiments [10]. The work also reveals what mechanisms limit the spin coherence time. Jelezko and his colleagues [3] present evidence indicating that the main culprit is the phonon-induced dynamical JT mechanism. As Atatüre and his colleagues argue, loss of coherence could also come from the fluctuating field produced by defect spins surrounding the SiV center.
Several strategies exist to counteract the contributions to dephasing. The phonon contribution could be reduced by shaping the diamond into a photonic band-gap structure, which would block the dynamic JT effect. Slow magnetic noise could be abated using dynamical decoupling schemes. Another interesting approach would be to replace the silicon- atom, which has a nuclear spin of zero, with the silicon- isotope, which has a spin- nucleus, and use the nuclear spin as a long-term quantum memory. Hyperfine levels on silicon- have already been identified by Jelezko and his colleagues [3] and methods exist to transfer qubits between electron and nuclear spins [11,12].
One application for SiV centers in a quantum network would be as quantum repeaters, whose function is to boost the information imprinted on photons. For this purpose, the SiV centers would need to have a spin coherence time approaching milliseconds, like that of the NV center. If this goal is reached, there is indeed hope that SiV centers could be used as a spin-photon interface in a future quantum network.
This research is published in Physical Review Letters.
References
- D. P. DiVincenzo, “The Physical Implementation of Quantum Computation,” Fortschr. Phys. 48, 771 (2000)
- H. J. Kimble, “The Quantum Internet,” Nature 453, 1023 (2008)
- Lachlan J. Rogers et al., “All-Optical Initialization, Readout, and Coherent Preparation of Single Silicon-Vacancy Spins in Diamond,” Phys. Rev. Lett. 113, 263602 (2014)
- Benjamin Pingault, Jonas N. Becker, Carsten H. H. Schulte, Carsten Arend, Christian Hepp, Tillmann Godde, Alexander I. Tartakovskii, Matthew Markham, Christoph Becher, and Mete Atatüre, “All-Optical Formation of Coherent Dark States of Silicon-Vacancy Spins in Diamond,” Phys. Rev. Lett. 113, 263601 (2014)
- T. P. Harty, D. T. C. Allcock, C. J. Ballance, L. Guidoni, H. A. Janacek, N. M. Linke, D. N. Stacey, and D. M. Lucas, “High-Fidelity Preparation, Gates, Memory, and Readout of a Trapped-Ion Quantum Bit,” Phys. Rev. Lett. 113, 220501 (2014)
- D. D. Awschalom, L. C. Bassett, A. S. Dzurak, E. L. Hu, and J. R. Petta, “Quantum Spintronics: Engineering and Manipulating Atom-Like Spins in Semiconductors,” Science 339, 1174 (2013)
- M. W. Doherty, N. B. Manson, P. Delaney, F. Jelezko, J. Wrachtrup, and L. C. L. Hollenberg, “The Nitrogen-Vacancy Colour Centre in Diamond,” Phys. Rep. 528, 1 (2013)
- E. Neu, D. Steinmetz, J. Riedrich-Möller, S. Gsell, M. Fischer, M. Schreck, and C.Becher, “Single Photon Emission from Silicon-Vacancy Colour Centres in Chemical Vapour Deposition Nano-Diamonds on Iridium,” New J. Phys. 13, 025012 (2011)
- E. Togan, Y. Chu, A. Imamoglu, and M. D. Lukin, “Laser Cooling and Real-Time Measurement of the Nuclear Spin Environment of a Solid-State Qubit,” Nature 478, 497 (2011); C. G. Yale, B. B. Buckley, D. J. Christle, G. Burkard, F. J. Heremans, L. C. Bassett, and D. D. Awschalom, “All-Optical Control of a Solid-State Spin Using Coherent Dark States,” Proc. Natl. Acad. Sci. U.S.A. 110, 7595 (2013)
- T. Müller, C. Hepp, B. Pingault, E. Neu, S. Gsell, M. Schreck, H. Sternschulte, D. Steinmüller-Nethl, C. Becher, and M. Atatüre, “Optical Signatures of Silicon-Vacancy Spins in Diamond,” Nature Commun. 5, 3328 (2014)
- M. V. G. Dutt, L. Childress, L. Jiang, E. Togan, J. Maze, F. Jelezko, A. S. Zibrov, P. R. Hemmer, and M. D. Lukin, ”Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond,” Science 316, 1312 (2007)
- G. D. Fuchs, G. Burkard, P. V. Klimov, and D. D. Awschalom, “A Quantum Memory Intrinsic to Single Nitrogen-Vacancy Centres in Diamond,” Nature Phys. 7, 789 (2011)