A Recipe for Error-Free Self-Assembly

Stephen Whitelam

Viewpoint

A Recipe for Error-Free Self-Assembly

Molecular Foundry, Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley, CA 94720, USA

June 11, 2014• Physics 7, 62

Computer simulations suggest that mixtures of hundreds of distinct nanoparticles or colloids can self-assemble into well-defined structures.

Figure caption — **Figure 1:** Self-assembling components, such as molecules or nanoparticles, have the potential to form materials with applications in nanotechnology and biology. Unfortunately, even under mild nonequilibrium conditions, mixtures of two components may not form a compositionally ordered structure because of kinetic traps. Reinhardt and Frenkel’s work shows that components of about $1000$ distinct types can avoid such kinetic traps, if component-type interactions are chosen correctly.

Molecular self-assembly—the organization of molecular components into ordered structures without external guidance—is a promising strategy for making complex materials that could be useful for nanotechnology or have biological applications. In 2012, researchers demonstrated that synthetic DNA strands called “DNA bricks” could self-assemble into complicated three-dimensional equilibrium structures, including letters of the English alphabet and shapes with well-defined cavities and tunnels [1]. The demonstration came as a great surprise to researchers in the field of DNA nanotechnology: the structures had formed from about $1000$ different types of DNA brick, yet the general expectation was that large numbers of component types would be unable to assemble in an error-free way [2]. Now, inspired by those experiments, Aleks Reinhardt and Daan Frenkel at the University of Cambridge in the UK, reporting in Physical Review Letters [3], have used computer simulations to reproduce this result without accounting for the specific molecular details of DNA. In doing so, they have demonstrated that a wide range of distinct components—from molecules to fabricated nanoparticles—could self-assemble into precisely defined structures.

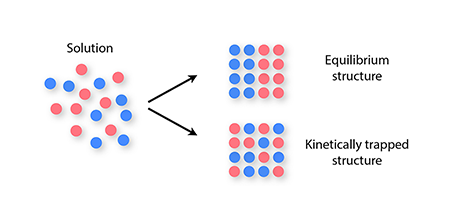
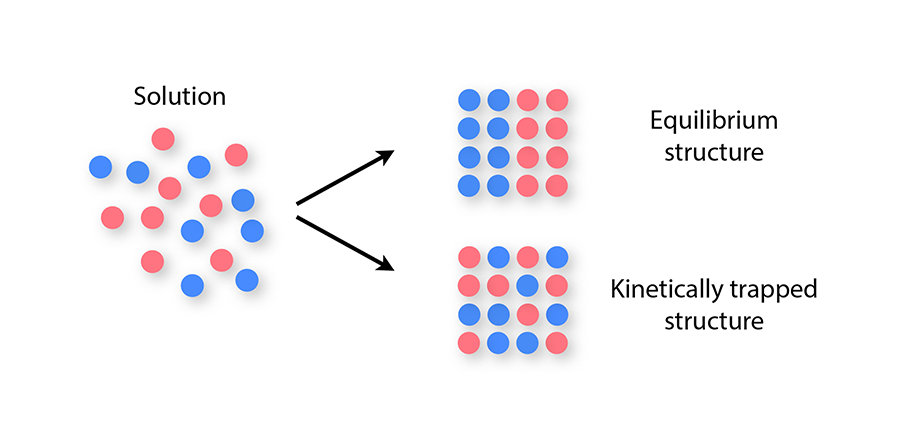
In general, the self-assembly of equilibrium structures is hindered by kinetic traps, which are nonequilibrium arrangements of components that evolve so slowly that the equilibrium structure may not appear on any time scale of interest to an experimenter. Kinetic traps are known to affect the self-assembly of even the simplest, idealized components, such as spheres bearing isotropic attractions. When cooled slowly, such components self-assemble into an equilibrium crystal, but when subjected to “harsh” nonequilibrium conditions, such as rapid and deep supercooling, they form disordered-looking structures [4,5]. These structures are kinetic traps, and they arise because strong interactions between particles prevent a disordered structure from relaxing to a crystal.

More complex materials consisting of two or more types of component—for example, sticky spheres bearing different charges, or DNA-based building blocks made from different DNA sequences—have a wider range of applications than do single-component materials. But with greater potential comes an increased susceptibility to kinetic traps during self-assembly: mixtures of many component types can become kinetically trapped even under mild nonequilibrium conditions, because of the long time scales associated with swapping two components once a solid has formed (Fig. 1). This slowness can prevent particles from achieving their equilibrium spatial arrangement as the structure they form nucleates and grows. This problem can occur even if the structure is an otherwise well-ordered crystal [6,7].

Given that some two-component mixtures become kinetically trapped while self-assembling, it would seem unlikely that many distinct component types could self-assemble into a compositionally defined equilibrium structure. However, Reinhardt and Frenkel show with computer simulations that this phenomenon can occur reproducibly. The authors model simple particles that interact via four tetrahedrally arranged sticky patches and use molecular simulations to observe the nucleation and growth of equilibrium crystal structures in which each particle type appears in only one defined position. Specifically, they show that structures containing about $1000$ different particles grow in an error-free way from nuclei only about $10$ particles in size.

The key to the success of Reinhardt and Frenkel’s assembly process is that a given sticky patch feels a strong attraction for only one particular sticky patch on one particular particle type, while the same patch feels only a weak attraction for any sticky patch that is not its intended partner. This patch-patch complementarity determines which particles are neighbors in the final structure and is similar to that of DNA strands [1]. However, while Reinhardt and Frenkel’s model was inspired by the DNA brick experiments [1], it accounts for patch-type complementarity only in a generic sense and does not represent any molecular details specific to DNA. Their results therefore suggest that the same phenomenon can be achieved in a range of experimental settings.

Why can $1000$ component types self-assemble directly into an equilibrium structure, while some two-component mixtures fall prey to kinetic traps? Reinhardt and Frenkel’s work suggests that successful self-assembly requires component types that can discriminate energetically between “native” contacts (contacts characteristic of the equilibrium structure) and “non-native” contacts (contacts that can form dynamically but are rare in equilibrium). Native contacts must be strong enough to encourage the desired ordered structure to grow, and, at the same time, non-native contacts must be weak enough that a jumbled structure of disordered component types cannot grow. Otherwise, we would expect kinetic trapping. Interactions mediated by single DNA strands can achieve these energetic requirements when $Q$ , the number of component types, is as large as $1000$ [1], but other types of interactions fail to do so even when $Q = 2$ [6,7].

Reinhardt and Frenkel’s strategy may have limits. One is the size of the final structure. The basic time scale for growth will likely increase in proportion to $Q$ , because only about $1$ in $Q$ component-component encounters can give rise to a native bond. Such time scales will become prohibitive well before reaching the macroscopic scale ( $Q \sim 10^{24}$ ). A second issue is that not every set of component interactions can be made as selective as those mediated by single DNA strands. An alternative strategy in such cases might be to develop theories to guide the self-assembly of structures whose component types are kinetically trapped in desirable ways [8–10].

Despite these challenges, Reinhardt and Frenkel’s findings should inspire researchers to try to assemble compositionally defined structures from a range of materials, such as nanoparticles or colloids. While it might seem odd to think about the crystallization of a multicomponent nanoparticle superlattice in the same terms as assembly of DNA nanostructures, this is exactly the perspective suggested by the modeling approach of Reinhardt and Frenkel: their simulations ignore the question of what components look like on the molecular scale, and resolve only the geometry and energy scales of component-type interactions. Match these characteristics, and you will likely replicate this phenomenon.

References

Y. Ke, L. L. Ong, W. M. Shih, and P. Yin, “Three-Dimensional Structures Self-Assembled from DNA Bricks,” Science 338, 1177 (2012)
K. V. Gothelf, “LEGO-like DNA Structures,” Science 338, 1159 (2012)
Aleks Reinhardt and Daan Frenkel, “Numerical Evidence for Nucleated Self-Assembly of DNA Brick Structures,” Phys. Rev. Lett. 112, 238103 (2014)
E. Zaccarelli, “Colloidal Gels: Equilibrium and Non-Equilibrium Routes,” J. Phys. Condens. Matter 19, 323101 (2007)
P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino, and D. A. Weitz, “Gelation of Particles with Short-Range Attraction,” Nature 453, 499 (2008)
A. Kim, R. Scarlett, P. Biancaniello, T. Sinno, and J. Crocker, “Probing Interfacial Equilibration in Microsphere Crystals Formed by DNA-Directed Assembly,” Nature Mater. 8, 52 (2008)
E. Sanz, C. Valeriani, D. Frenkel, and M. Dijkstra, “Evidence for Out-of-Equilibrium Crystal Nucleation in Suspensions of Oppositely Charged Colloids,” Phys. Rev. Lett. 99, 55501 (2007)
B. Peters, “Competing Nucleation Pathways in a Mixture of Oppositely Charged Colloids: Out-of-Equilibrium Nucleation Revisited,” J. Chem. Phys. 131, 244103 (2009)
D. Stauffer, “Kinetic Theory of Two-Component (“Hetero-Molecular”) Nucleation and Condensation,” J. Aerosol Sci. 7, 319 (1976)
S. Whitelam, L. O. Hedges, and J. D. Schmit, “Self-Assembly at a Nonequilibrium Critical Point,” Phys. Rev. Lett. 112, 155504 (2014)

About the Author

Stephen Whitelam is a scientist at the Molecular Foundry at Lawrence Berkeley National Laboratory. He and his group use statistical mechanics to investigate pattern formation and self-assembly at the nanoscale. He received his Ph.D. in theoretical physics from Oxford University in 2004, where he worked with Juan P. Garrahan and David Sherrington. He did postdoctoral work from 2004 to 2007 with Phillip L. Geissler at University of California, Berkeley, and from 2007 to 2008 with Nigel Burroughs at Warwick University.