Emerging Quantum Order in an Expanding Gas

Stephen R. Clark

Viewpoint

Emerging Quantum Order in an Expanding Gas

Department of Physics, University of Bath, Claverton Down, Bath BA2 7AY, United Kingdom

October 19, 2015• Physics 8, 99

The spontaneous emergence of long-range quantum order, normally the preserve of low-temperature equilibrium states, has been observed in an expanding cloud of potassium atoms.

Figure caption — **Figure 1:** In Schneider and colleagues’ experiment, a long one-dimensional lattice chain of potassium atoms (blue spheres) is prepared in a state where lattice sites at the center are filled with precisely one atom each, and the rest is empty. The grey parabolas represent the lattice’s potential wells. Upon lowering the depth of the wells, so the atoms can hop, the atoms ballistically expand to the left and right and bunch up in the momentum states $k = \pm 𝜋 ∕ 2 a$ , where $a$ is the lattice spacing. The time-dependent momentum distribution of the atoms illustrates how, from an initially flat profile, two sharp peaks emerge that correspond to the enhanced occupation of these states.

In the everyday world, being “far from equilibrium” is a common state of affairs. In biology it is crucial for life. In economics it is the driving force for market activity. In many-body physics it generates a near-endless zoo of complex effects, rich both conceptually and phenomenologically. Indeed, nonequilibrium physics encompasses many fields including the cosmology of the early Universe [1], quark-gluon jet production in heavy-ion collisions [2], glass formation in dense fluids [3], and laser-driven symmetry breaking in solids [4, 5]. Yet questions about nonequilibrium phenomena can often appear untameable, because the nonequilibrium effects lack a universal organizing principle. For this reason, experiments on the dynamics of quantum systems that can be controlled at a microscopic level and are well isolated from their environment have become increasingly important for obtaining concrete answers [6–8].

In a new study, Ulrich Schneider, from the Ludwig Maximilian University of Munich in Germany, and colleagues have used a cold atomic gas to carefully realize, for the first time, a nonequilibrium phenomenon known as dynamical quasicondensation [9]. This is where delicate quantum long-range order, normally the hallmark of low-temperature equilibrium systems, is seen to spontaneously emerge in an expanding gas. Their experiment convincingly verifies this phenomenon, opening the door to further studies in more complex systems. It also creates enticing links to other phenomena such as thermalization and equilibration.

Long-range order takes place when remote portions of a physical system are correlated in some way. For instance, a crystalline solid has long-range order due to the regular arrangement of its constituent atoms. But order can come in many forms and, moreover, can be quantum mechanical in origin. Bose-Einstein condensation is one such example. In these systems, below a certain temperature, the statistics of bosons conspire to make them all bunch up in the same quantum ground state. The resulting equilibrium state then possesses long-range phase ordering. This means that if matter waves from two distant parts of the system overlap, interference fringes will appear. True condensation requires such ordering to be independent of distance. However, if bosons are constrained to move around in a two-dimensional (2D) plane or one-dimensional (1D) tube, they are said to form quasicondensates instead, because their long-range phase ordering drops off with distance as a power law.

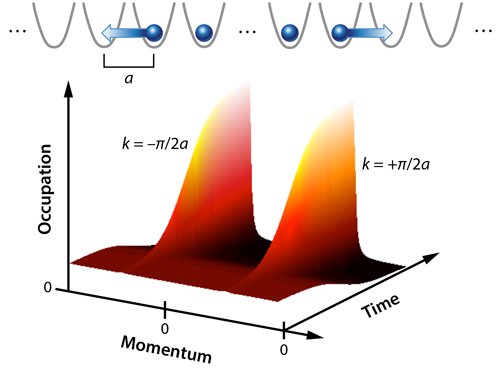
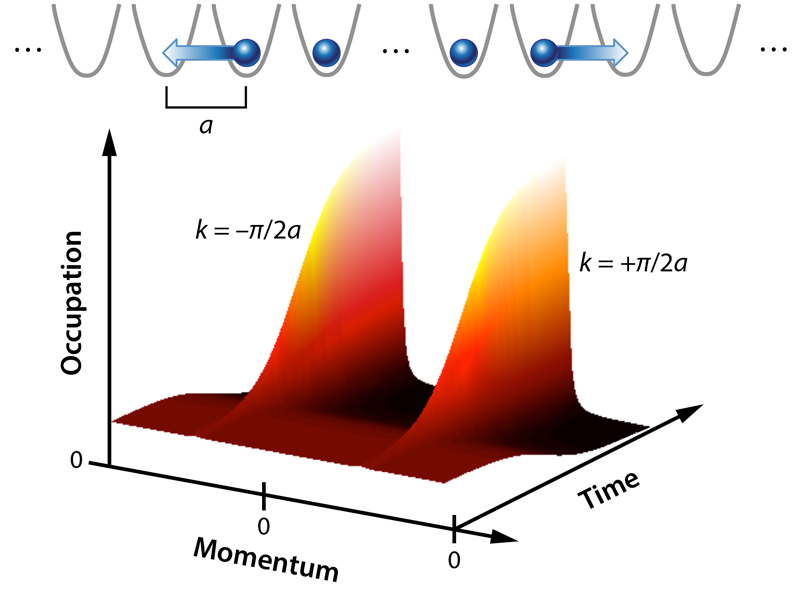
In 2004, Marcos Rigol and Alejandro Muramatsu [10] predicted that in a 1D setting a quasicondensate of bosons could emerge dynamically. They considered a 1D lattice populated with bosons that can hop between neighboring sites. Importantly, these bosons were required to strongly repel each other, preventing any two from being on the same site—a feature that gains them the name of “hard-core bosons.” Next, they took the initial state of the system to have a central region with one boson located on each site, surrounded by an otherwise empty and infinitely large lattice. This state is highly excited and evolves in time, with the bosons suddenly expanding into the empty regions. They found that this expansion quickly results in a 50:50 split of the bosons occupying the momentum states $k = \pm 𝜋 ∕ 2 a$ , where $a$ is the lattice spacing. Consequently, the bosons bunch up to form quasicondensates traveling to the left and right at the only finite momenta consistent with energy conservation [10].

To cleanly realize and measure the delicate effects of dynamical quasicondensation, Schneider and colleagues exploited and refined several techniques in the field of cold atoms. Specifically, they prepared a Bose-Einstein condensate of around 100,000 bosonic potassium atoms and then slowly loaded them into a three-dimensional (3D) periodic arrangement of laser light known as an optical lattice. For low laser intensities, the potential wells of the lattice are shallow, and atoms will tunnel between sites, delocalizing themselves over the whole system. However, as the laser intensity increases, the potential wells deepen. This deepening suppresses the tunneling and confines atoms more tightly, increasing repulsion between atoms that occupy the same site. For sufficiently deep lattices, the atoms will localize on different sites because of this repulsion, making the system an insulator.

By combining a deep lattice with additional shallow trapping of the cloud, Schneider and colleagues created a region at the center with one atom per site, surrounded by empty sites. To ensure this was achieved with high precision, they also employed a magnetic field to enhance the repulsion between the atoms. Having prepared this initial state, the researchers then rapidly lowered the laser intensity along one axis, thereby transforming the system into a 2D array of independent 1D chains. The resulting lower lattice depth allowed atoms to hop along the chains, and a magnetic field was again used to preserve their strong repulsion so they remained hard core. Additional laser beams cancelled out the shallow confinement along the chain axis so that the atomic expansion occurred in a potential that was as flat as possible. The atoms then expanded ballistically. By imaging the absorption of light shone through the cloud, the authors measured the in situ density of the atoms with time.

Finally, after the expansion, the researchers removed all of the trapping and used the technique of time-of-flight imaging to reconstruct the momentum distribution of the cloud. Crucially, they applied a short laser pulse before this measurement to temporarily increase the lattice depth along the chains and enhance the visibility of structure at higher momenta. With these innovations, they observed, for the longest expansion times considered, distinct peaks in the momentum distribution very close to $k = \pm 𝜋 ∕ 2 a$ (Fig. 1). The peaks indicate a large occupation of those states, and they are in remarkable agreement with theoretical predictions of quasicondensation.

What is most intriguing about Schneider and colleagues’ experiment is that it provides yet further evidence of how nonequilibrium phenomena can defy common intuition [6–8]. Generally, the time evolution of a highly excited initial state is expected to result in a cacophony of excitations that eventually make any local patch of the system appear indistinguishable from a thermal state with the same average energy [11]. That a seemingly messy expansion of hard-core bosons in one dimension can instead reorganize itself into a pair of quasicondensates is striking. That it has been observed experimentally is extraordinary and confirms an important example of the dynamical emergence of long-range order.

Many fascinating open questions remain, such as whether dynamical quasicondensation manifests in 2D or 3D systems, perhaps realizing an atom-laser source, and whether it extends to more generic systems than hard-core bosons. From a conceptual viewpoint, the dynamical emergence of quasicondensates from an initially insulating state has suggestive connections to light-induced superconductivity, which also occurs in close proximity to an insulating state [4, 5]. Future work may reveal whether there are deeper principles controlling emerging order far from equilibrium.

This research is published in Physical Review Letters.

References

A. B. Linde, Particle Physics and Inflationary Cosmology (Harwood Academic, Chur, 1990)[Amazon][WorldCat].
J. Berges, K. Boguslavski, S. Schlichting, and R. Venugopalan, “Universality Far from Equilibrium: From Superfluid Bose Gases to Heavy-Ion Collisions,” Phys. Rev. Lett. 114, 061601 (2015).
L. Berthier and J. Kurchan, “Non-Equilibrium Glass Transitions in Driven and Active Matter,” Nature Phys. 9, 310 (2013).
D. Fausti, R. I. Tobey, N. Dean, S. Kaiser, A. Dienst, M. C. Hoffmann, S. Pyon, T. Takayama, H. Takagi, and A. Cavalleri, “Light-Induced Superconductivity in a Stripe-Ordered Cuprate,” Science 331, 189 (2011).
W. Hu, S. Kaiser, D. Nicoletti, C. R. Hunt, I. Gierz, M. C. Hoffmann, M. Le Tacon, T. Loew, B. Keimer, and A. Cavalleri, “Optically Enhanced Coherent Transport in $Y B a_{2} C u_{3} O_{6.5}$ by Ultrafast Redistribution of Interlayer Coupling,” Nature Mater. 13, 705 (2014).
Toshiya Kinoshita, Trevor Wenger, and David S. Weiss, “A Quantum Newton's Cradle,” Nature 440, 900 (2006).
S. Hofferberth, I. Lesanovsky, B. Fischer, T. Schumm, and J. Schmiedmayer, “Non-Equilibrium Coherence Dynamics in One-Dimensional Bose Gases,” Nature 449, 324 (2007).
J. P. Ronzheimer, M. Schreiber, S. Braun, S. S. Hodgman, S. Langer, I. P. McCulloch, F. Heidrich-Meisner, I. Bloch, and U. Schneider, “Expansion Dynamics of Interacting Bosons in Homogeneous Lattices in One and Two Dimensions,” Phys. Rev. Lett. 110, 205301 (2013).
L. Vidmar, J. P. Ronzheimer, M. Schreiber, S. Braun, S. S.Hodgman, S. Langer, F. Heidrich-Meisner, I. Bloch, and U. Schneider, “Dynamical Quasicondensation of Hard-Core Bosons at Finite Momenta,” Phys. Rev. Lett. 115, 175301 (2015).
M. Rigol and A. Muramatsu, “Emergence of Quasicondensates of Hard-Core Bosons at Finite Momentum,” Phys. Rev. Lett. 93, 230404 (2004).
J. Eisert, M. Friesdorf, and C. Gogolin, “Quantum Many-Body Systems out of Equilibrium,” Nature Phys. 11, 124 (2015).

About the Author

Stephen R. Clark is a Senior Lecturer in Theoretical Physics at the University of Bristol. He completed his doctoral studies at the University of Oxford in 2007. He has subsequently held research fellowships at the Centre for Quantum Technologies in the National University of Singapore and at Keble College, Oxford, as well as a senior scientist post at the Clarendon Laboratory in the University of Oxford. Before joining Bristol in 2018, he was a Lecturer in physics at the University of Bath. His research focuses on the dynamical properties of driven strongly correlated many-body systems ranging from cold atoms to high-temperature superconductors.