Spin Control
Computer simulations aren’t always the best way to learn about dangerous oscillations in an airplane wing or a bridge component, but physical experiments are difficult to control when the oscillations become unstable. A procedure reported in the 20 June Physical Review Letters can gently nudge an oscillating object into its unstable regime, where researchers can check theoretical predictions of its behavior. The research team’s system periodically pushed a rigid pendulum under the control of a computer algorithm that included “feedback” from sensing the pendulum’s motion. The new algorithm could lead to more realistic testing of future components over a wide range of conditions.
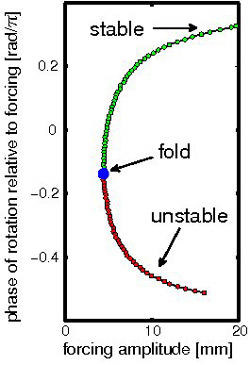
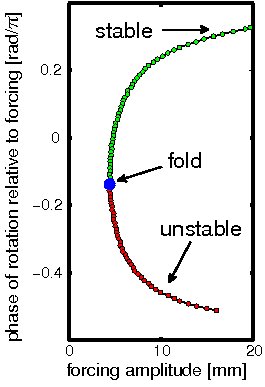
The problem with mathematical and computational models of vibrating components such as auto parts is that it’s hard to accurately account for every bit of friction and every possible bend and twist. But in a real physical experiment, there are “unstable” oscillations that are hard to find and maintain, and sometimes they lead to damage. Imagine twirling a Hula Hoop by moving your hips in the same direction as the hoop and then switching to an “antiphase” oscillation, where your hips are forward when the hoop is back. Even if you can get to this unstable state, it’s hard to maintain because it’s very sensitive to small changes in your hip motion that can destroy it. Researchers have been able to maintain some classes of unstable oscillations in experiments, but to reliably reach the Hula Hoop variety, they would need to move smoothly from a stable oscillation to one that’s unstable and find the crossover point–the “fold”–that divides the two regimes.
To solve this problem, Jan Sieber of the University of Aberdeen in Scotland and his colleagues built a standard type of feedback control system but came up with a new computer algorithm to run it. In the experiment, a piston drives a pivot up and down three times per second, which spins the attached pendulum in complete circles, like a propeller. The system detects the pendulum’s motion, and the computer uses that data in the algorithm that controls both the amplitude of the piston oscillation and its timing. In the stable rotating state, the pivot is up when the pendulum is up; in the unstable rotating state, the pivot is down when the pendulum is up.
The team started by driving the pendulum in stable rotations. To move it to the unstable state, their algorithm contained two new elements. First, it gradually changed the driving amplitude in a way that always allowed the pendulum to “catch up” with the new piston motion at each step. The algorithm always kept the “effort” needed to control the piston motion close to zero. Second, they adapted a method used in computer simulations for getting past the fold that separates stable from unstable motion. This technique moves the system very slowly through the fold and allows the timing difference between piston and pendulum oscillations–the phase difference–to change rapidly near the fold, without changing the amplitude much at all.
The researchers’ data on the pendulum’s fold agreed well with a theoretical model. “This method is useful if you find it is difficult to write down a mathematical model that describes the experiment accurately,” says co-author Bernd Krauskopf of the University of Bristol. “If you just run the experiment it will automatically go around the fold even if you don’t know where it is.”
Michael Thompson of the Centre for Mathematical Sciences at Cambridge University has great expectations for this type of dynamic testing. “If it’s a delicate piece of equipment, this allows you to effectively test it without damaging it,” he says. “Then they can effectively derive a mathematical model from the real model.”
–Mike Wofsey
More Information
article on stable and unstable oscillations in Hula-Hooping: R. Balasubramaniam and M. T. Turvey, “Coordination Modes In the Multisegmental Dynamics Of Hula Hooping,” Biol. Cybern. 90, 176-190 (2004)