Diversity Breeds Conformity
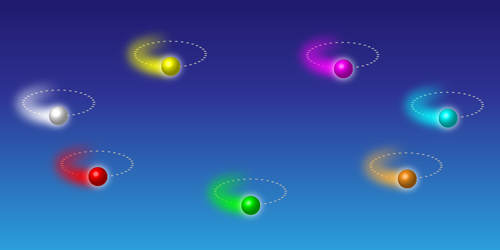
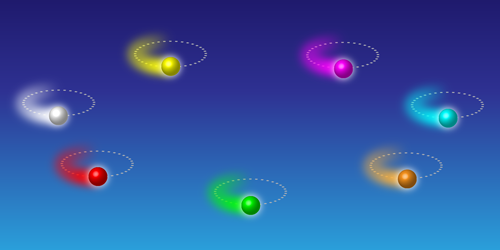
Place a row of identical metronomes on a suspended platform and their ticking pendulums will eventually unite in a synchronous swing. This spectacular display occurs because the platform couples the oscillators such that the forces generated by one ticking metronome shift the phase of the tick of the others. A duo of theorists has now discovered a surprising twist on the phenomenon. Takashi Nishikawa and Adilson Motter at Northwestern University, Illinois, devised a model in which a synchronized state can arise—and is only stable—if each oscillator is different from the others.
The researchers’ model consisted of a circle of seven coupled oscillators—each akin to a small ball traveling in an elliptical orbit. When the model parameters describing each oscillator’s motion were identical, the initially synchronized oscillators quickly fell out of step with one another, and their collective movements resembled a Mexican wave traveling around the circle. However, the oscillators could reach a stable synchronized state if the parameters for each oscillator were shifted so that they were no longer the same. This change effectively freezes the traveling wave, causing the oscillators to move in synchrony. Nishikawa and Motter suggest that this so-called asymmetry-induced symmetry could be behind biological symmetries in nature, like in yeast cells, which develop from asymmetric buds.
This research is published in Physical Review Letters.
–Katherine Wright
Katherine Wright is a Contributing Editor for Physics.