Light Bends Itself into an Arc
Apart from the broadening effects of diffraction, light beams tend to propagate along a straight path. Mirrors, lenses, and light guides are all ways to force light to take a more circuitous path, but an alternative that many researchers are exploring is to prepare light beams that can bend themselves along a curved path, even in vacuum. In a paper in Physical Review Letters, Ido Kaminer and colleagues at Technion, Israel, report on wave solutions to Maxwell’s equations that are both nondiffracting and capable of following a much tighter circular trajectory than was previously thought possible [1]. Apart from fundamental scientific interest, such wave solutions may lead to the possibility of synthesizing shape-preserving optical beams that make curved left- or right-handed turns on their own. The equations describing these light waves could also be generalized to describe similar behavior in sound and water waves.
The idea for making specially shaped light waves that could bend without dispersion actually emerged from quantum physics. In 1979, Berry and Balazs realized that the force-free Schrödinger equation could give rise to solutions in the form of nonspreading “Airy” wave packets [2] that freely accelerate even in the absence of any external potential. This early work remained dormant in the literature for decades, until Christodoulides and co-workers demonstrated the optical analog of Airy wave packets: specially shaped beams of light that did not diffract over long distances but could bend (or, self-accelerate) sideways [3] (see 28 November 2007 Focus story ). Such self-accelerating Airy beams have since attracted a great deal of interest due to their unique properties, and they provide the basis for a number of proposed applications including optical micromanipulation [4], plasma guidance and light bullet generation [5], and routing surface plasmon polaritons [6] (see 6 September 2011 Viewpoint ).
A typical simplification when solving Maxwell’s wave equations is to assume the light waves are paraxial, meaning the angle between the wave vectors that constitute a wavepacket and the optical axis is small enough that the wave does not deviate too much from its propagation direction. Under this paraxial approximation, the resulting time-independent scalar Helmholtz equation takes the same form of the Schrödinger equation, and it was this relationship that led to the proposal that finite-power optical Airy beams could be attainable in experiments [3]. (Unlike other nondiffracting beams such as the well-known Bessel beams [7], Airy beams have a unique spatial phase structure, do not rely on simple conical superposition of plane waves, and can self-accelerate.) At small angles, Airy beams follow parabolic trajectories similar to ballistic projectiles moving under the force of gravity [8], but at large angles, beyond the paraxial approximation, they cannot maintain their shape-preserving property as they propagate. Therefore, it is important to identify mechanisms that could allow self-accelerating beams to propagate in a true diffraction-free manner even for large trajectory bending.
Several studies have searched for accelerating beams beyond the paraxial regime. In one study [9], nonparaxial Airy beams were sought as exact solutions of Maxwell’s wave equation, but these beams tend to break up and decay as they propagate because parts of them consist of evanescent waves. In yet another study [10], the so-called caustic method was used to effectively stretch the paraxial Airy beams to the nonparaxial regime, but these “caustic-designed” accelerating beams don’t preserve their shape like nondiffracting paraxial Airy beams. Thus, a natural question arose: Could a beam accelerate at large nonparaxial angles but still hold its shape? Since beam propagation is governed by Maxwell’s equations, it was equivalent to asking: Were there any solutions to Maxwell’s equations that allowed nondiffracting, self-accelerating beams?
In their new work, Kaminer et al. report they have found shape-preserving nonparaxial accelerating beams (NABs) as a complete set of general solutions to the full Maxwell’s equations. Differently from the paraxial Airy beams that accelerate along a parabolic trajectory, these nonparaxial beams accelerate in a circular trajectory.
To find the solutions for the NABs, Kaminer et al. started with the scalar Maxwell’s wave equation for a given polarization, such as TE (transverse electric) polarization, where the electric field is perpendicular to the direction of the wave. Since the equation exhibits full symmetry between the and coordinates, the solutions of shape-preserving beams must have circular symmetry. The authors therefore transformed the equation into polar coordinates and looked for shape-preserving solutions where the field amplitude didn’t vary with angle. In polar coordinates, the solution to the wave equation is a Bessel function; transforming back to Cartesian coordinates, the solution must be separated into forward and backward propagating waves in Fourier space. However, only the forward propagating part forms the desired accelerating beam, so the Kaminer et al. solutions are properly called “half Bessel wave packets.”
The authors found a solution for TM (transverse magnetic) polarization through a similar procedure. For both TE and TM polarizations, the beams preserve their shape while the quarter-circle bending could occur after a propagation distance of just . In addition, the authors studied the properties of these Bessel-like accelerating beams and found that the Poynting vector of the main lobe can turn by more than [1].
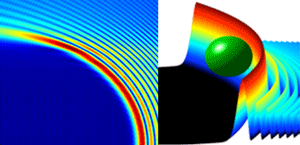
The left part of Fig. 1 shows a typical solution of the shape-preserving beam, which can sweep out a quarter circle. It is important to note that this one-dimensional beam propagates initially along the longitudinal direction while its curved trajectory in the - plane is determined by a Bessel function. This is quite different from the traditional nondiffracting Bessel beam, which propagates in a straight line while its two-dimensional transverse pattern follows a Bessel function [7].
As the authors point out, the nonparaxial shape-preserving accelerating beams found in their work originates from the full vector solutions of Maxwell’s equation. Moreover, in their scalar form, these beams are the exact solutions for nondispersive accelerating wave packets of the most common wave equation describing time-harmonic waves. As such, this work has profound implications for other linear wave systems in nature, ranging from sound waves and surface waves in fluids to many kinds of classical waves. Furthermore, based on previous successful demonstrations of self-accelerating Airy beams [3–6], one would expect that the nonparaxial Bessel-like accelerating beams proposed in this study could be readily realized in experiment. Apart from many exciting opportunities for these beams in various applications, such as beams that self-bend around an obstacle (Fig. 1, right), one might expect one day light could really travel around a circle by itself, bringing the search for an “optical boomerang” into reality.
References
- I. Kaminer, R. Bekenstein, J. Nemirovsky, and M. Segev, Phys. Rev. Lett. 108, 163901 (2012)
- M. V. Berry and N. L. Balazs, Am. J. Phys. 47, 264 (1979)
- G. A. Siviloglou and D. N. Christodoulides, Opt. Lett. 32, 979 (2007); G. A. Siviloglou, J. Broky, A. Dogariu, and D. N. Christodoulides, Phys. Rev. Lett. 99, 213901 (2007)
- J. Baumgartl, M. Mazilu, and K. Dholakia, Nature Photon. 2, 675 (2008)
- P. Polynkin, M. Kolesik, J. V. Moloney, G. A. Siviloglou, and D. N. Christodoulides, Science 324,229 (2009); A. Chong, W. H. Renninger, D. N. Christodoulides, and F. W. Wise, Nature Photon. 4,103 (2010)
- P. Zhang, S. Wang, Y. Liu, X. Yin, C. Lu, Z. Chen, and X. Zhang, Opt. Lett. 36,3191 (2011); A. Minovich, A. E. Klein, N. Janunts, T. Pertsch, D. N. Neshev, and Y. S. Kivshar, Phys. Rev. Lett. 107,116802 (2011); L. Li, T. Li, S. M. Wang, C. Zhang, and S. N. Zhu, 107,126804 (2011)
- J. Durnin, J. J. Miceli, Jr., and J. H. Eberly, Phys. Rev. Lett. 58,1499 (1987)
- G. A. Siviloglou J. Broky, A. Dogariu, and D. N. Christodoulides, Opt. Lett. 33,207 (2008); Y. Hu, P. Zhang, C. Lou, S. Huang, J. Xu, and Z. Chen, 35,2260 (2010)
- A. V. Novitsky and D. V. Novitsky, Opt. Lett. 34, 3430 (2009)
- L. Froehly, F. Courvoisier, A. Mathis, M. Jacquot, L. Furfaro, R. Giust, P. A. Lacourt, and J. M. Dudley, Opt. Express 19,16455 (2011)