Neural Networks Identify Topological Phases
A detailed characterization of phases of matter is at the forefront of research in condensed-matter and statistical physics. Although physicists have made incredible progress in the characterization of a wide variety of phases, the identification of novel topological phases remains challenging. Now, Yi Zhang and Eun-Ah Kim from Cornell University, New York [1], have taken a big-data approach to tackling this problem. In their work, thousands of microscopic “images” or “snapshots” of a phase, created using a special topography procedure, are fed into a machine-learning algorithm that is trained to decide whether these images come from a topological or a conventional phase of matter—exactly as modern computer vision algorithms are designed to tell cats from dogs in a picture.
Traditionally, phases of matter are differentiated by their symmetry properties [2]. For example, water in its liquid and vapor forms is more spatially symmetric on average than in its solid counterpart, in which water molecules form crystal structures. Also, ferromagnets, which are often found holding notes on refrigerator doors, are magnetically ordered materials that, upon heating, transition to a more magnetically symmetric state in which they lose their ability to stick to some metallic surfaces. By contrast, topological phases of matter are distinguished through more abstract mathematical constructions called topological invariants. These are linked to large-scale features of objects [2]. For instance, if viewed by a topologist’s eyes, a doughnut is the same as a coffee cup, because they both have just one hole. But a pretzel, which has two or three holes in it, is a topologically different object. In other words, the number of holes is a topological invariant. Amazingly, similar topological fingerprints emerge in real materials and in theoretical models of condensed-matter phases, such as quantum Hall states, topological insulating phases, spin liquids, and many other examples [2] (see Collection on Topological Phases). But the unequivocal identification of these topological markers, both in experiments and simulations, remains hard. The experiments require challenging electronic transport and interference measurements, as well as in situ images, of the materials that host the topological phases, whereas the simulations require numerically intensive calculations.
To identify conventional phases, physicists typically rely on theoretical ideas such as the order parameter, which represents the degree to which a physical system is ordered, as well as on experimental quantities such as the specific heat [2]. For topological phases, which often lack local order parameters, physicists appeal instead to specific response functions and surface states [2, 3], or when available, to nonlocal properties such as quantum entanglement [4].
More recently, however, there has been a concerted effort towards applying machine-learning ideas to the classification and identification of phases in condensed-matter physics [5–10]. Preliminary results suggest that conventional machine-learning algorithms, including those based on neural networks, automatically discover order parameters such as the material’s magnetization or other physically plausible local quantities [5, 6, 9]. But for topological phases, the algorithms fail [6, 7], require the explicit presence of edge states [8], or rely on nongeneric details of the models under study [6, 9]. Thus they can’t clearly “see” the fingerprints of topological phases.
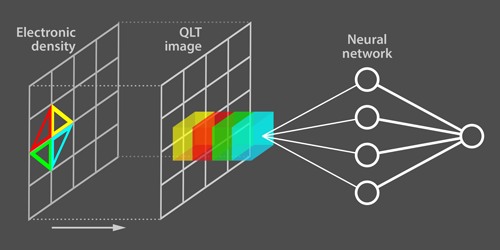
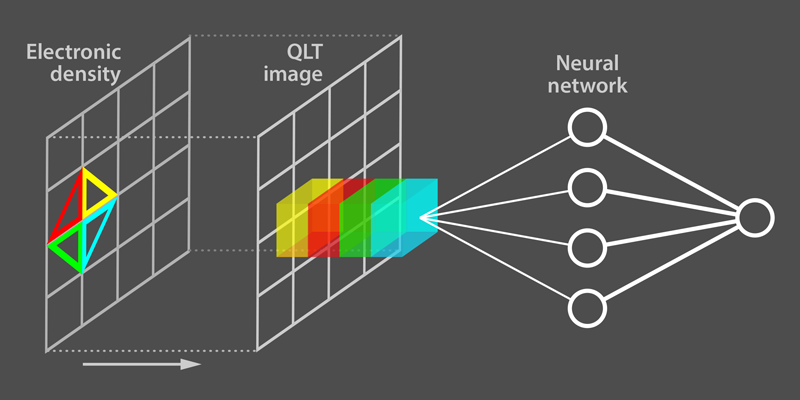
Zhang and Kim propose a “cure” to the topological nearsightedness of machine-learning algorithms based on neural networks. Dubbed quantum loop topography (QLT), the cure involves constructing multidimensional images that highlight topological information about the phases that is otherwise invisible to the networks. The researchers tested the procedure on a conventional insulator and two types of Chern insulator—a system of electrons that hosts a quantum Hall topological phase in the absence of a magnetic field. They built the QLT images of the different insulating phases using snapshots of the density of the phases obtained from their electronic wave functions. The mathematics behind the QLT images closely follows a special formula for the Hall conductivity, which is the response function that characterizes Chern insulators. For all phases, pixels in the QLT image are based on several adjacent, triangular loops located at the pixels of the phase’s density snapshots (Fig. 1). The authors considered triangles of increasing size until enough nonlocal information about a particular phase was encoded in its QLT image. They then fed the QLT images into a standard neural network that was trained to judge whether the different images corresponded to a topological phase or not. They found that the procedure could successfully tell a Chern insulating phase from a conventional one with high fidelity, regardless of the microscopic details of the phases. What’s more, the approach could identify quantum phase transitions between the different phases.
The wave function of a many-electron system, which is at the heart of the authors’ approach, is one of the most complex mathematical objects in physics. It contains vast amounts of information, so deriving and analyzing it is the ultimate big-data challenge for physicists. It is thus reasonable to expect that machine-learning techniques will help to perform these and other related tasks. Zhang and Kim capitalized on this idea and proposed a solution to identify topological states.
Zhang and Kim’s QLT approach is a timely addition to the expanding toolbox of machine-learning algorithms for tackling problems in condensed-matter and statistical physics. For one, the technological applications that topological phases may find, such as topological quantum computing and spintronics, are becoming more visible. For another, snapshots of many-body wave functions are becoming routinely available through the use of experimental techniques such as quantum-gas microscopy [11] and quantum annealing [12]. Thus, besides being an interesting theoretical exercise, the authors’ QLT strategy and other related machine-learning tools may well become practical tools for the identification and exploration of matter in all its possible forms.
This research is published in Physical Review Letters.
References
- Y. Zhang and E.-A. Kim, “Quantum Loop Topography for Machine Learning,” Phys. Rev. Lett. 118, 216401 (2017).
- X. Wen, Quantum Field Theory of Many-Body Systems: From the Origin of Sound to an Origin of Light and Electrons, Oxford Graduate Texts (Oxford University Press, Oxford, 2004)[Amazon][WorldCat].
- N. Goldman, J. C. Budich, and P. Zoller, “Topological Quantum Matter with Ultracold Gases in Optical Lattices,” Nat. Phys. 12, 639 (2016).
- M. Levin and X.-G. Wen, “Detecting Topological Order in a Ground State Wave Function,” Phys. Rev. Lett. 96, 110405 (2006).
- L. Wang, “Discovering Phase Transitions with Unsupervised Learning,” Phys. Rev. B 94, 195105 (2016).
- J. Carrasquilla and R. G. Melko, “Machine Learning Phases of Matter,” Nat. Phys. 13, 431 (2017).
- W. Hu, R. R. P. Singh, and R. T. Scalettar, “Discovering Phases, Phase Transitions and Crossovers through Unsupervised Machine Learning: A Critical Examination,” arXiv:1704.00080.
- T. Ohtsuki and T. Ohtsuki, “Deep Learning the Quantum Phase Transitions in Random Two-Dimensional Electron Systems,” J. Phys. Soc. Jpn. 85, 123706 (2016).
- P. Ponte and R. G. Melko, “Kernel Methods for Interpretable Machine Learning of Order Parameters,” arXiv:1704.05848.
- S. J. Wetzel, “Unsupervised Learning of Phase Transitions: From Principal Component Analysis to Variational Autoencoders,” arXiv:1703.02435.
- W. S. Bakr, J. I. Gillen, A. Peng, S. Fölling, and M. Greiner, “A Quantum Gas Microscope for Detecting Single Atoms in a Hubbard-Regime Optical Lattice,” Nature 462, 74 (2009).
- M. W. Johnson et al., “Quantum Annealing with Manufactured Spins,” Nature 473, 194 (2011).