A Ranking Scheme for Mass-Transport Predictions
Understanding and controlling the transport of atoms and molecules is paramount to the design of many modern devices. These include batteries, where fast ion transport is beneficial, and nanoscale semiconductor components for electronics, where the transport of dopants must be limited. The current understanding of these transport processes is based on the Nobel-prize-winning work of Lars Onsager [1, 2]. In a pair of 1931 papers, he related the flux of an entity like density, heat, or concentration to a corresponding driving force like a difference in pressure, temperature, or chemical potential. The connection between flux and force, he showed, was a tensor of transport coefficients that characterizes how a system responds to a departure from equilibrium. Unfortunately, while elegant, Onsager’s theory does not provide a practical recipe for computing the coefficient values. So, instead, researchers approximate them using a slew of theories and numerical schemes [3–5]. Comparing, assessing, and improving upon these approximation methods has been a challenge in materials science, but a new theory proposed by Dallas Trinkle of the University of Illinois at Urbana–Champaign provides a powerful conceptual framework for accomplishing all three tasks [6].
The difficulty in obtaining reliable transport coefficients lies in a mismatch of scales. Consider the case of mass transport in a solid, which occurs because of gradients in the chemical potentials of different species. Onsager expressed his equations for mass transport at the mesoscale, assuming concentrations and chemical potentials that vary smoothly over a much longer length scale than the spacing between atoms. But accurate transport models require a knowledge of relevant microscopic “units,” and there is an extremely large number of microscopic configurations that must be considered. For instance, in a battery, the unit process that contributes to transport is the hopping around of an ion, and the rate of the hopping may depend strongly on the presence of neighboring ions or defects. Brute-force computations of the Onsager coefficients that are rooted in microscopic processes can be highly accurate because they involve averages over many configurations, but this averaging is also extremely time consuming. In contrast, analytic techniques can approximate the coefficients cheaply by, say, assuming that some local configurations dominate the transport. But the accuracy of these cheaper schemes can be difficult to assess. The tension between cost and accuracy comes into play, for example, when searching for battery materials in a large database. One wants to be able to make a lot of fast predictions but not at the expense of missing a diamond in the rough.
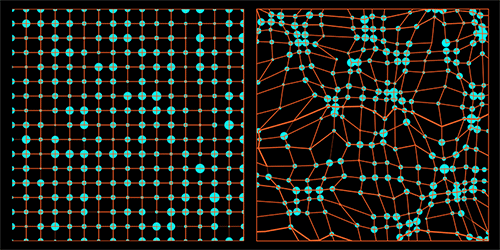
Trinkle provides a new approach to assessing different methods of approximating mass-transport coefficients. He considers a generic solid through which multiple atomic species can diffuse. He then introduces a fictitious displacement field that—if it existed—would warp the space in which the diffusing atoms are embedded (Fig. 1). Next, Trinkle obtains an expression for the Onsager coefficients that depends on the virtual atom displacements (see note in Ref. [7]). His expression yields the correct transport coefficients for the unwarped solid when the displacement field assumes one particular, or “optimal,” form. But with any other form of the field, the expression produces larger coefficient values. (This idea is akin to the variational principle in quantum physics, which says that the energy of an arbitrary wave function is always greater than or equal to that of the ground state wave function.) According to Trinkle’s approach, finding the correct coefficients amounts to an optimization problem: one varies the form of the displacement field until the coefficients are minimized.
Trinkle’s work leads to a new perspective: approximating the transport coefficients corresponds to putting “constraints” on the form of the displacement field. This idea has several implications. First, an approximation method will never predict transport coefficients that globally minimize Trinkle’s variational expression if the method corresponds to a set of fields that don’t include the optimal field. Second, the larger the predicted coefficients compared to the coefficients that minimize the variational expression, the more approximate the predictions are. This fact gives a natural way to assess and rank different methods, even when the exact values of the coefficients are not known.
Such a ranking system will make it easier to assess whether new, affordable computational approaches are accurate. It also offers a way to systematically improve the accuracy of computed coefficients without having to derive new physical models—a process that has tended to be a bit of a black art. How might this improvement work? One would start with the set of constrained fields that corresponds to some approximated coefficients. Then, one would gradually relax the constraints to find an updated field that is closer to being optimal. Finally, this improved field would be plugged into the variational expression to determine more accurate coefficients. This way of finding more accurate coefficients might provide less physical intuition compared with a traditional transport model, but it can be implemented much more systematically.
This research is published in Physical Review Letters.
References
- L. Onsager, “Reciprocal relations in irreversible processes. I.,” Phys. Rev. 37, 405 (1931).
- L. Onsager, “Reciprocal relations in irreversible processes. II.,” Phys. Rev. 38, 2265 (1931).
- M. Nastar, V. Y. Dobretsov, and G. Martin, “Self-consistent formulation of configurational kinetics close to equilibrium: The phenomenological coefficients for diffusion in crystalline solids,” Philos. Mag. A 80, 155 (2000).
- K. D. Belashchenko and V. G. Vaks, “The master equation approach to configurational kinetics of alloys via the vacancy exchange mechanism: general relations and features of microstructural evolution,” J. Phys. Cond. Matt. 10, 1965 (1998).
- R. Kikuchi, “The path probability method,” Prog. Theor. Phys. Suppl. 35, 1 (1966).
- D. Trinkle, “Variational principle for mass transport,” Phys. Rev. Lett. 121, 235901 (2018).
- Trinkle’s variational expression considers only a subset of the Onsager coefficients (the diagonal ones from the coefficient tensor). A second step is needed to determine the others.