A Hot Topic in the Quantum Hall Effect
Around 40 years ago, physicists stumbled on an elegant recipe for creating exotic phases of matter: Pour electrons into a clean two-dimensional environment, add a magnetic field, and allow to cool. Out comes a dazzling variety of so-called fractional quantum Hall phases. Certain types of fractional quantum Hall phases, called non-Abelian, provide a potential platform for intrinsically error-resistant quantum computation. However, unambiguously identifying these phases poses a notorious challenge for experimentalists, as measurements often do not uniquely pinpoint which of several candidate phases is present.
Experiments published last month [1] provide direct evidence that a previously studied quantum Hall phase first observed long ago [2] is indeed non-Abelian. In a delightful surprise, the observations appear to rule out the two leading candidate phases that were expected from theory! Now David Mross and colleagues from the Weizmann Institute of Science in Israel [3] and Chong Wang and colleagues from Harvard University [4] describe a possible resolution: Because of disorder, the system might harbor patches of each of the two theoretically expected candidates, which combine to form a distinct non-Abelian phase compatible with observations. Further work is required to ascertain whether experiments conform to this scenario, but the idea of new phases emerging from hybrids of competing states could prove useful in the broader search for non-Abelian systems.
The fractional quantum Hall effect is a variation of the classical Hall effect that occurs when a metal is exposed to a magnetic field. Classically, the Hall conductivity —defined as the ratio of the electrical current to the induced transverse voltage—changes smoothly as the field strength increases. But in high-quality two-dimensional systems such as gallium arsenide quantum wells or graphene, the Hall conductivity instead features plateaus quantized at , where is the electron charge, is Planck’s constant, and is a rational number. Measuring a plateau with noninteger signals the onset of a fractional quantum Hall phase.
Fractional quantum Hall phases give birth to new quasiparticles called anyons with no standard-model counterpart. Paradoxically, anyons behave like electrons—which are indivisible—diced into smaller bits; more precisely, anyons can carry a fraction of an electron charge and exhibit peculiar forms of quantum exchange statistics that are strikingly different from that of ordinary bosons and fermions. In non-Abelian phases, the exchange statistics dictates that swapping pairs of anyons can actually reshuffle the system among different wavefunctions. This strange behavior is more than mere curiosity: The swapping or “braiding” of these anyons can be exploited to manipulate quantum information in a manner that is inherently protected from errors. Fractional quantum Hall phases also host novel “one-way streets” for charge and heat flow at their boundaries. Crucially, their one-way nature sharply suppresses scattering events, in turn leading to quantization of and other transport coefficients. The detailed structure of these “edge states” relates intimately to the kinds of anyons that emerge, so studying the flows along these one-way streets reveals information about the types of anyons within the material.
Researchers have long suspected that the observed fractional quantum Hall phase with in gallium arsenide samples [2] is non-Abelian. The problem is that the measured value doesn’t uniquely specify which phase appears. In fact, infinitely many fractional quantum Hall phases exhibit the same and hence ; they differ in the types of edge states and anyons that they host. Theory usually singles out a small set of “natural” candidates—some that are non-Abelian and others that are not. For the case, numerical simulations [5] have favored two candidate non-Abelian phases called the Pfaffian [6] and anti-Pfaffian [7].
One way to discriminate among candidate phases with the same value is to consider the edge states and how they conduct heat. Edge-state heat transport is revealed through measurements of the thermal Hall conductivity , which specifies the transverse temperature gradient accompanying a heat current and takes the form in fractional quantum Hall phases [8]. Here is the Boltzmann constant, is the sample temperature, and is a rational number. Most importantly here, a noninteger value of is believed to unambiguously imply a non-Abelian phase. For example, the Pfaffian and anti-Pfaffian phases for the case exhibit and , respectively.
In their tour de force experiment published last month [1], Mitali Banerjee and collaborators (some of whom are coauthors on the Mross et al. paper) performed the first-ever measurement of at and indeed found a half-integer , which is an extraordinary triumph in light of implications for fundamental science and quantum computing. Curiously, however, they report , suggesting the appearance of an alternative non-Abelian phase dubbed the PH-Pfaffian [9]. Unlike the theoretically motivated Pfaffian and anti-Pfaffian phases, evidence in favor of the PH-Pfaffian is wholly absent from simulations. So how could the latter emerge in experiment?
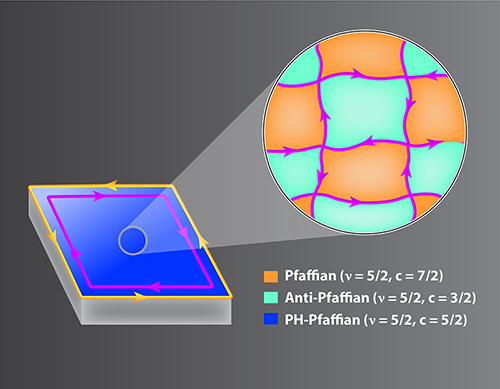
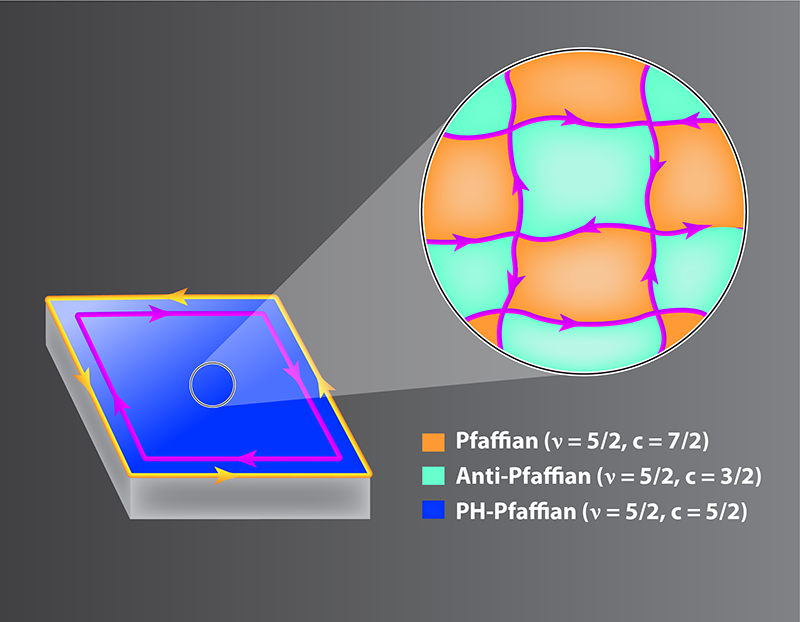
Mross et al. [3] and Wang et al. [4] postulate that Pfaffian and anti-Pfaffian phases indeed appear experimentally—in harmony with numerical simulations—but not uniformly across the sample. Instead, random potential variations stabilize the Pfaffian in some regions and anti-Pfaffian in others, producing a kind of non-Abelian patchwork quilt. Wherever Pfaffian and anti-Pfaffian patches meet, their respective edge states couple, leaving one-way streets that allow heat to flow but not electrical charge. Consequently, the seams of the non-Abelian patchwork quilt form a network of neutral heat-carrying channels that extend across the sample (Fig. 1). What, then, is the fate of this network when the channels interact with each other, for instance at vertices? The work by Mross et al. and Wang et al. (see also Ref. [10]) shows that, under certain conditions, interactions within the network can convert the system as a whole into the PH-Pfaffian. Other phases are also possible, however, including a novel “thermal metal” with quantized but nonquantized .
In terms of the kinds of anyons that they support, Pfaffian, anti-Pfaffian, and PH-Pfaffian phases provide equally good platforms for quantum computing. Nevertheless, phases stabilized by disorder might be relatively fragile compared to “clean” realizations, which could limit utility for applications. In any case, at present it is unclear whether the conditions needed for the PH-Pfaffian to emerge in the above scenario are operative in Banerjee et al.’s experiment. An alternative interpretation has recently been debated that does not involve the PH-Pfaffian at all, but rather it invokes subtleties with thermal equilibration [11]. Regardless of the ultimate explanation, the works highlighted here raise intriguing issues for future research. A disordered arrangement of two competing states begetting a third phase is a fascinating possibility in its own right and may be relevant elsewhere in the quantum Hall problem. The potential existence of distinct “hybrid” states also suggests that caution is warranted when drawing conclusions from clean-system simulations when multiple phases sit very close in energy. Alternative means of stabilizing the PH-Pfaffian also warrant investigation as stressed by Wang et al. [4]. One natural direction is to explore trial wave functions for the PH-Pfaffian phase, but subtle challenges face this tried-and-true method [12]. There may be more surprises yet to come in this ever-rich problem.
This research is published in Physical Review Letters, Physical Review B, and Nature.
References
- M. Banerjee, M. Heiblum, V. Umansky, D. E. Feldman, Y. Oreg, and A. Stern, “Observation of Half-Integer Thermal Hall conductance,” Nature (2018).
- R. Willett, J. P. Eisenstein, H. L. Störmer, D. C. Tsui, A. C. Gossard, and J. H. English, “Observation of an Even-Denominator Quantum Number in the Fractional Quantum Hall Effect,” Phys. Rev. Lett. 59, 1776 (1987).
- D. F. Mross, Y. Oreg, A. Stern, G. Margalit, and M. Heiblum, “Theory of Disorder-Induced Half-Integer Thermal Hall Conductance,” Phys. Rev. Lett. 121, 026801 (2018).
- C. Wang, A. Vishwanath, and B. I. Halperin, “Topological Order from Disorder and the Quantized Hall Thermal Metal: Possible Applications to the State,” Phys. Rev. B 98, 045112 (2018).
- See, e.g., E. H. Rezayi, “Landau Level Mixing and the Ground State of the Quantum Hall Effect,” Phys. Rev. Lett. 119, 026801 (2017).
- G. Moore and N. Read, “Non-Abelions in the Fractional Quantum Hall Effect,” Nucl. Phys. B 360, 362 (1991).
- M. Levin, B. I. Halperin, and B. Rosenow, “Particle-Hole Symmetry and the Pfaffian State,” Phys. Rev. Lett. 99, 236806 (2007); S.-S. Lee, S. Ryu, C. Nayak, and M. P. A. Fisher, “Particle-Hole Symmetry and the Quantum Hall State,” 99, 236807 (2007).
- C. L. Kane and M. P. A. Fisher, “Quantized Thermal Transport in the Fractional Quantum Hall Effect,” Phys. Rev. B 55, 15832 (1997); A. Cappelli, M. Huerta, and G. R. Zemba, “Thermal Transport in Chiral Conformal Theories and Hierarchical Quantum Hall States,” Nucl. Phys. B 636, 568 (2002).
- D. Thanh Son, “Is the Composite Fermion a Dirac Particle?,” Phys. Rev. X 5, 031027 (2015).
- B. Lian and J. Wang, “Theory of the Disordered Quantum Thermal Hall State: Emergent Symmetry and Phase Diagram,” Phys. Rev. B 97, 165124 (2018).
- S. H. Simon, “Interpretation of Thermal Conductance of the Edge,” Phys. Rev. B 97, 121406 (2018); D. E. Feldman, “Comment on S. H. Simon, Interpretation of Thermal Conductance of the Edge,” arXiv:1805.03204.
- R. V. Mishmash, D. F. Mross, J. Alicea, and O. I. Motrunich, “Numerical Exploration of trial Wavefunctions for the Particle-Hole-Symmetric Pfaffian,” arXiv:1804.01107.